Fractal-Streets

本文主要是介绍Fractal-Streets，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

title: Fractal Streets
date: 2023-12-13 14:48:45
tags: 分形
categories: 算法进阶指南

题目大意

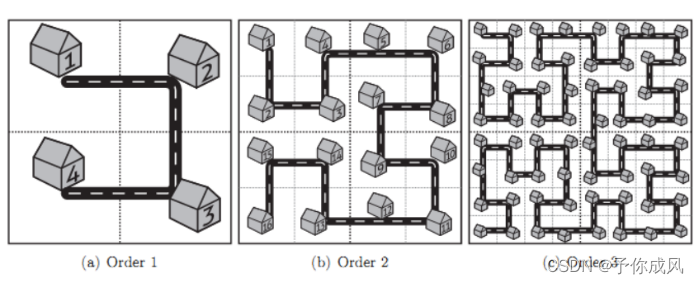
将原来的城市复制一遍放在原城市的上方，将原城市顺时针90°放在原城市的左上方，将逆时针90°后的城市放在原城市的左边，然后用道路将四部分链接起来，反复进行相同操作。

解题思路

这是著名的通过一定规律无限包含自身的“分形”图。为了方便计算，我们把标号从 $0$ 开始
解题关键就是，求编号为 $M$ 的房屋在 $N$ 级城市的位置，把问题转化为 calc(N,M),因此改题目转化为求 $calc(N,A)$ 与 $calc(N,B)$ 的距离。
在求解 $calc(N,M)$ 时，因为 $N-1$ 级城市有 $2^{2\ast N-2}$ 座房屋，所以我们先求解 $calc(N-1,Mmod{2}^{2\ast N-2})$,根据房屋编号 M 与 该级数的房屋总数确定编号上下左右位置。
在这里插入图片描述

代码实现

#include<bits/stdc++.h>using namespace std;typedef long long LL;const int N = 1314;const int MOD = 9901;typedef pair<LL,LL> PII;PII calc(LL n,LL m)
{if(n == 0) return make_pair(0,0);LL len = 1ll << (n - 1),cnt = 1ll << (2 * n - 2);//每一级的半长和多少个 1 级的 PII pos = calc(n - 1,m % cnt);LL x = pos.first, y = pos.second;LL z = m / cnt;if(z == 0) return make_pair(y,x);else if(z == 1) return make_pair(x,y + len);else if(z == 2) return make_pair(x + len,y + len);else  return make_pair(2 * len - y - 1,len - x - 1);
}
int main()
{int t; cin >> t;while(t --){LL N,A,B;cin >> N >> A >> B;PII a = calc(N,A - 1),b = calc(N,B - 1);LL x = a.first - b.first, y = a.second - b.second;cout << fixed << setprecision(0) << sqrt(x * x + y * y) * 10 << endl; } 
}

这篇关于Fractal-Streets的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---