本文主要是介绍HDOJ 4506 小明系列故事——师兄帮帮忙(腾讯专场,快速幂),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
http://acm.hdu.edu.cn/showproblem.php?pid=4506
小明系列故事——师兄帮帮忙
Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 65535/32768 K (Java/Others)Total Submission(s): 5563 Accepted Submission(s): 1510
Problem Description
小明自从告别了ACM/ICPC之后,就开始潜心研究数学问题了,一则可以为接下来的考研做准备,再者可以借此机会帮助一些同学,尤其是漂亮的师妹。这不,班里唯一的女生又拿一道数学题来请教小明,小明当然很高兴的就接受了。不过等他仔细读题以后,发现自己也不会做,这下小明囧了:如果回复说自己不懂,岂不是很没面子?
所以,他现在私下求你帮忙解决这道题目,题目是这样的:
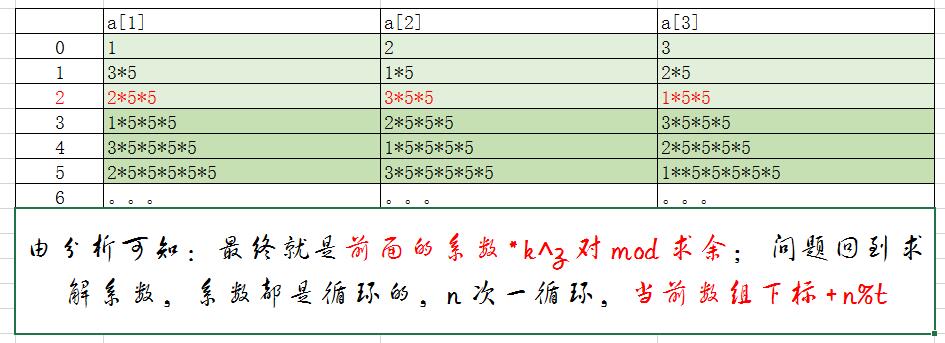
给你n个数字,分别是a1,a2,a3,a4,a5……an,这些数字每过一个单位时间就会改变,假设上一个单位时间的数字为a1’,a2’,a3’……an’,那么这个单位时间的数字a[i] = a[i - 1]’ * K(i == 1的时候a[1] = a[n]’ * K),其中K为给定的系数。
现在的问题就是求第t单位时间的时候这n个数字变成了什么了?由于数字可能会很大,所以只要你输出数字对10^9 + 7取余以后的结果。
所以,他现在私下求你帮忙解决这道题目,题目是这样的:
给你n个数字,分别是a1,a2,a3,a4,a5……an,这些数字每过一个单位时间就会改变,假设上一个单位时间的数字为a1’,a2’,a3’……an’,那么这个单位时间的数字a[i] = a[i - 1]’ * K(i == 1的时候a[1] = a[n]’ * K),其中K为给定的系数。
现在的问题就是求第t单位时间的时候这n个数字变成了什么了?由于数字可能会很大,所以只要你输出数字对10^9 + 7取余以后的结果。
Input
输入数据第一行是一个正整数T,表示有T组测试数据;
每组数据有两行,第一行包含输入三个整数n, t, k,其中n代表数字个数,t代表第t个单位时间,k代表系数;第二行输入n个数字ai,代表每个数字开始的时候是多少。
[Technical Specification]
T <= 100
1 <= n <= 10 ^ 4
0 <= t <= 10 ^ 9 其中 t = 0 表示初始状态
1 <= k <= 10 ^ 9
1 <= ai<= 10 ^ 9
每组数据有两行,第一行包含输入三个整数n, t, k,其中n代表数字个数,t代表第t个单位时间,k代表系数;第二行输入n个数字ai,代表每个数字开始的时候是多少。
[Technical Specification]
T <= 100
1 <= n <= 10 ^ 4
0 <= t <= 10 ^ 9 其中 t = 0 表示初始状态
1 <= k <= 10 ^ 9
1 <= ai<= 10 ^ 9
Output
对于每组数据请输出第t单位时间后这n个数字变成了什么,输出的时候 每两个数字之间输出一个空格,行末不要输出多余的空格,具体见样例。
Sample Input
2 3 2 5 1 2 3 3 0 5 1 2 3
Sample Output
50 75 25 1 2 3
Source
2013腾讯编程马拉松初赛第一场(3月21日)
思路:
这个题目卡的时间是最长的,可能之前思路是错的,卡在了找最终系数的问题上,
最后只能够 ko blog.。
最后附上自己的不完善的思路。
AC CODE:
#include<stdio.h>
#include<cstring>
#include<algorithm>
#define HardBoy main()
#define ForMyLove return 0;
using namespace std;
const int MYDD = 11030;
const int MOD = 1e9+7;int PowQuick(int a, int n, int mod) {int ans = 1;while(n > 0) {if(n&1) ans = ((long long)ans*a) % mod;/*KILL BUG -> ((long long)(ans*a)) */a = ((long long)a*a) % mod;/*注意范围溢出*//*KILL BUG -> ((long long)(a*a))*/n >>= 1;}return (int)ans;
}int HardBoy {int tt;scanf("%d", &tt);while(tt--) {int a[MYDD], n, t, k;scanf("%d %d %d", &n, &t, &k);for(int j = 1; j <= n; j++) {scanf("%d", &a[j]);}int ans[MYDD];int getpow = PowQuick(k,t, MOD);for(int i = 1; i <= n; i++) {/*note*/ans[i] = ((long long)a[i]*getpow)%MOD;ans[i] = (int)ans[i];}t = t%n;int x = n-t+1;if(x > n) x = x%n;for(int j = x; j <= n; j++) {if(j == x) printf("%d",ans[j]);else printf(" %d",ans[j]);}for(int j=1; j < x; j++)printf(" %d",ans[j]);printf("\n");}ForMyLove
}错误 ->
CODE WRONG :
#include<stdio.h>
#include<cstring>
#include<algorithm>
#define HardBoy main()
#define ForMyLove return 0;
using namespace std;
const int MYDD = 11030;
const int MOD = 1e9+7;int PowQuick(int a, int n, int mod) {int ans = 1;while(n > 0) {if(n&1) ans = (ans*a) % mod;a = (long long)(a*a) % mod;/*注意范围溢出*/n >>= 1;}return ans;
}int HardBoy {int tt;scanf("%d", &tt);while(tt--) {int a[MYDD], n, t, k;scanf("%d %d %d", &n, &t, &k);int getpow = PowQuick(k, t, MOD);for(int j = 1; j <= n; j++) {scanf("%d", &a[j]);}int ans[MYDD];t = t%n;for(int j = 1; j <= n; j++) {int biao = j+n%t;if(j == n) {int biao = (j+n%t)%n;if(n == t) biao = n;ans[j] = ((a[biao] % MOD) * getpow) % MOD;} else {ans[j] = ((a[biao] % MOD) * getpow) % MOD;}printf("ans[%d] -> j:%d \n", j, biao);}for(int j = 1; j < n; j++) {printf("%d ", ans[j]);}printf("%d\n", ans[n]);}ForMyLove
}
/*
6
3 1 5
1 2 3*/
这篇关于HDOJ 4506 小明系列故事——师兄帮帮忙(腾讯专场,快速幂)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!