本文主要是介绍Intelij之如何同时启动同一个应用的多个实例,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
[版权申明] 非商业目的注明出处可自由转载
出自:shusheng007
文章目录
- 概述
- 具体方法
- 总结
概述
现如今后端处于微服务统治时代,如果你们家服务没有用到微服务都不好意思和人家打招呼,感觉自己技术低人一等。不管怎么说我相信存在即合理这句话,如果一个事物不合理,那么这个事物就一定会消失在历史的长河中的,所以这块不准备讨论这些没有意义的问题,只讨论具体问题
如何在Intelij里启动同一个应用的多个实例?
具体方法
- 打开
Edit Configurations的弹窗 - 选中你要启动的应用,然后勾选右边的
Allow parallel run选项, - 在启动参数中配置你要启动实例的端口,例如此处的
-Dserver.port=9082 - 点击apply按钮,点击ok按钮
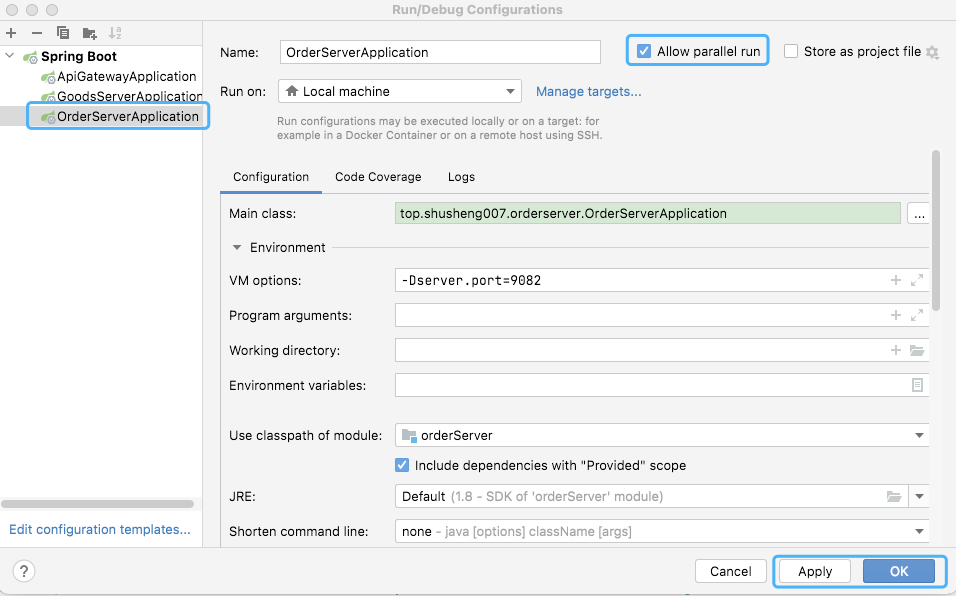
-
点击运行按钮,一个新实例就会启动
-
启动第二个时,还是进入
Edit Configuration弹窗,在启动参数中将端口修改为另一个值,点击应用并确定后,再次点击运行按钮,如下图所示。

那个运行按钮上就会显示现在IDEA运行着几个实例。
总结
成功了就点个赞再走吧…
这篇关于Intelij之如何同时启动同一个应用的多个实例的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





