本文主要是介绍基于matlab实现老照片的简单修复,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
照片可以承载许多信息,是我们保存历史的一个重要载体,它们记录了过去的人、事、物,是我们了解历史、追溯过去的重要资料。大部分照片随着时间的流逝,会出现老化、损坏、污染、褪色、模糊等问题变成常说的老照片,照片修复就是对因各种因素导致的照片质量下降进行修复,尽可能恢复照片的原貌。下面以matlab为工具,对部分老照片进行简单修复,并通过修复结果看是否达到了预期。
基本思路如下,采用matlab作为工具,通过读入图像,对彩色图像进行图像增强,图像平滑、图像锐化,以及使用一些的算法进行一定的计算处理,结合部分滤波器,如均值滤波器,高斯低通滤波器等,对图像进行处理从而达到修复图像色彩、去除图像污染等的目的。预期达到的结果是,能够使图像的色彩尽可能地恢复成原图像,若没有原图像作为参照,则尽可能恢复为图像内事物的常见状态,且尽可能地去除图像的黑点污染,得到一个干净、色彩清晰的图像。以修复照片为目的,通过算法解决所需修复的问题。
首先,由于照片的色彩退化,所以先对其进行色彩对比度增强的处理,色彩对比度增强可通过HSI和RGB增强两种方法来实现
HSI图像增强的代码如图:

RGB图像增强的代码如下:
RGB = (im_e);
R = RGB(:,:,1);
G = RGB(:,:,2);
B = RGB(:,:,3);%三个通道分别进行色度增强
Y = 0.299 * R + 0.587 * G + 0.114 * B;
U = 128 - 0.168736 * R - 0.331264 * G + 0.5 * B;
V = 128 + 0.5 * R - 0.418688 * G - 0.081312 * B;
YUV=cat(3,Y,U,V); %合并三个图像为RGB图像y_img = YUV(:,:,1);
u_img = YUV(:,:,2);
v_img = YUV(:,:,3);y_int = adapthisteq(y_img);
v_int = adapthisteq(v_img);Y = single(y_int(:,:,1));
U = single(u_img(:,:,1));
V = single(v_int(:,:,1));C = Y - 16;
D = U - 128;
E = V - 128;% seprate RGb
R = uint8((298 * C + 409 * E + 128) / 256);
G = uint8((298 * C - 100 * D - 208 * E + 128) / 256);
B = uint8((298 * C + 516 * D + 128) / 256);% Return Color RGB
color_rgb(:,:,1) = R;
color_rgb(:,:,2) = G;
color_rgb(:,:,3) = B;figure;
subplot(1,2,1);
imshow(color_rgb,[]);title('彩色图像增强');个人比较推荐彩色图像的RGB色彩增强的算法
处理后的结果如下:
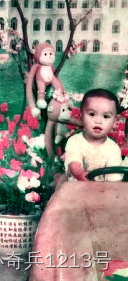
根据处理后的结果可以看出,色彩恢复较好,但发现处理后有一些噪声,关于图像的降噪滤波的方式有很多,例如维纳滤波、均值滤波、中值滤波、高斯滤波等,个人也尝试了很多,大部分都不适合该图片的降噪,偶然间发现了SurFace Blur算法,其与均值滤波结合使用,达到了较理想的降噪效果。
均值滤波的实验代码如下:
%均值滤波
for i=1:12
I=color_rgb;
OutImg=color_rgb;
R=I(:,:,1);
G=I(:,:,2);
B=I(:,:,3);R=filter2(fspecial('average',3),R)/255;
G=filter2(fspecial('average',3),G)/255;
B=filter2(fspecial('average',3),B)/255;
I2= cat(3,R,G,B); %对彩色图像R,G,B三个通道分别进行3×3模板的均值滤波
end%figure;
subplot(1,2,2);imshow(I2);
title('均值滤波')imwrite(I2,'均值滤波.jpg');SurFace Blur算法的代码如下:
A=imread('均值滤波.jpg');%A:读入图像
r=5; %r:半径
T=10; %T:阈值
w=zeros(2*r+1,2*r+1); %模板矩阵的尺寸%图像初始化处理figure;subplot(1,2,1);
imshow(A);title('原图');
% img=rgb2gray(A); %图像灰度化
%
% img=double(img); %转为矩阵
R=double(A(:,:,1));
G=double(A(:,:,2));
B=double(A(:,:,3));
%各通道图像
[m,n]=size(R);
imgn=zeros(m+2*r,n+2*r); %创建一个长宽各增加[2r]的扩容矩阵
imgn(r+1:r+m,r+1:r+n)=R;imgn(1:r,r+1:r+n)=R(1:r,1:n); %上边界填充
imgn(1:m+r,n+r+1:n+2*r)=imgn(1:m+r,n+1:n+r); %右边界填充
imgn(m+r+1:m+2*r,r+1:n+2*r)=imgn(m+1:m+r,r+1:n+2*r); %下边界填充
imgn(1:m+2*r,1:r)=imgn(1:m+2*r,r+1:2*r); %左边界填充
[m1,n1]=size(G);
imgn1=zeros(m1+2*r,n1+2*r); %创建一个长宽各增加[2r]的扩容矩阵
imgn1(r+1:r+m1,r+1:r+n1)=G;imgn1(1:r,r+1:r+n1)=G(1:r,1:n1); %上边界填充
imgn1(1:m1+r,n1+r+1:n1+2*r)=imgn1(1:m1+r,n1+1:n1+r); %右边界填充
imgn1(m1+r+1:m1+2*r,r+1:n1+2*r)=imgn1(m1+1:m1+r,r+1:n1+2*r); %下边界填充
imgn1(1:m1+2*r,1:r)=imgn1(1:m1+2*r,r+1:2*r); %左边界填充[m2,n2]=size(B);
imgn2=zeros(m2+2*r,n2+2*r); %创建一个长宽各增加[2r]的扩容矩阵
imgn2(r+1:r+m2,r+1:r+n2)=B;imgn2(1:r,r+1:r+n2)=B(1:r,1:n2); %上边界填充
imgn2(1:m2+r,n2+r+1:n2+2*r)=imgn2(1:m2+r,n2+1:n+r); %右边界填充
imgn2(m2+r+1:m2+2*r,r+1:n2+2*r)=imgn2(m2+1:m2+r,r+1:n2+2*r); %下边界填充
imgn2(1:m2+2*r,1:r)=imgn2(1:m2+2*r,r+1:2*r); %左边界填充
%开始计算每个像素,共计算m*n次
for i=r+1:r+mfor j=r+1:r+n %遍历imgn 中部的源img部分%计算式子的分母w=1-abs(imgn(i-r:i+r,j-r:j+r)-imgn(i,j))/(2.5*T); %w是一个以img中的元素为核心,size=[2r+1][2r+1]的矩阵,这样的模板会计算m*n次
%灰度值溢出检查for p=1:2*r+1 for q=1:2*r+1 if w(p,q) <=0w(p,q)=0;endendend%计算式子的分子s=w.*imgn(i-r:i+r,j-r:j+r); %计算总式imgn(i,j)=sum(sum(s))/sum(sum(w)); %一个sum()对一维数组求和,sum(sum())就是对二维矩阵求和end
end
for i=r+1:r+m1for j=r+1:r+n1 %遍历imgn 中部的源img部分%计算式子的分母w1=1-abs(imgn1(i-r:i+r,j-r:j+r)-imgn1(i,j))/(2.5*T); %w是一个以img中的元素为核心,size=[2r+1][2r+1]的矩阵,这样的模板会计算m*n次
%灰度值溢出检查for p=1:2*r+1 for q=1:2*r+1 if w1(p,q) <=0w1(p,q)=0;endendend%计算式子的分子s1=w1.*imgn1(i-r:i+r,j-r:j+r); %计算总式imgn1(i,j)=sum(sum(s1))/sum(sum(w1)); %一个sum()对一维数组求和,sum(sum())就是对二维矩阵求和end
end
for i=r+1:r+m2for j=r+1:r+n2 %遍历imgn 中部的源img部分%计算式子的分母w2=1-abs(imgn2(i-r:i+r,j-r:j+r)-imgn2(i,j))/(2.5*T); %w是一个以img中的元素为核心,size=[2r+1][2r+1]的矩阵,这样的模板会计算m*n次
%灰度值溢出检查for p=1:2*r+1 for q=1:2*r+1 if w2(p,q) <=0w2(p,q)=0;endendend%计算式子的分子s2=w2.*imgn2(i-r:i+r,j-r:j+r); %计算总式imgn2(i,j)=sum(sum(s2))/sum(sum(w2)); %一个sum()对一维数组求和,sum(sum())就是对二维矩阵求和end
end
img=imgn(r+1:r+m,r+1:r+n); %从imgn截取出源img部分
img1=imgn1(r+1:r+m1,r+1:r+n1); %从imgn截取出源img部分
img2=imgn2(r+1:r+m2,r+1:r+n2); %从imgn截取出源img部分
res=cat(3,img,img1,img2);
%figure;
subplot(1,2,2);
imshow(uint8(res));title('SurfaceBlur算法后');滤波后的图像如下所示:

对比发现噪声减少了,但边缘不够清晰,因此,要实现图像的边缘清晰化算法,个人尝试过空域滤波与频域滤波,最后决定使用同态滤波法。
其参考代码如下
histgram=zeros(1,256); %生成直方图数组并置0
cdf=zeros(1,256);
d=1;
n=2;
%img=(imread('hofi.bmp'));
img=input; [r, c]=size(img(:,:,1));
A=zeros(r,c);
H=zeros(r,c);
for i=1:r for j=1:c R=(((i-r/2).^2+(j-c/2).^2)).^(.5); H(i,j)=1/(1+(d/R)^(2*n)); end
end alphaL=0.1;
aplhaH=1.01;
H=((aplhaH-alphaL).*H)+alphaL;
H=1-H;
im_e=img;for k=1:3im_l=log2(1+double(img(:,:,k)));
im_f=fft2(im_l);
im_nf=H.*im_f;
im_n=abs(ifft2(im_nf)); im_e1=exp(im_n)-1;
max_im=max(im_e1(:));
min_im=min(im_e1(:));
im_e2=uint8(1+(250/(max_im-min_im))*(im_e1-min_im));
im_e(:,:,k)=1.65*(im_e2-100);
end
figure(1)
subplot(1,2,1);imshow(img); title('(a)原始图像');if size(img, 3) > 1G = im2double(rgb2gray(img));
elseG = im2double(img);
end
F = fftshift(fft2(G)); %将图像中心移到中间
subplot(1,2,2);imshow(im_e);title('(c)同态滤波后的增强图像');
if size(im_e, 3) > 1G = im2double(rgb2gray(im_e));
elseG = im2double(im_e);
end
F = fftshift(fft2(G)); %将图像中心移到中间
imF = log10(abs(F)+1);处理结果如下:

边缘略微清晰了,但图片色彩变弱,于是,调整一下处理顺序,先使用同态滤波来使边缘清晰化,再进行色彩增强与图像的降噪滤波,最后再锐化一下。处理结果如下

放上原图进行对比

经过对比可知,实验效果良好,基本实现了基础的修复。
本次实验没有使用图像的灰度化进行处理,原因之一就是灰度化后图像的色彩恢复不太理想也不太还原,在原来色调的基础上进行修复较为简便与实用。
大部分的代码都是拼接起来。
完整的代码如下:若打不开第一个连接可尝试第二个链接
http://链接:https://pan.baidu.com/s/1mfwrBDqIrsxI3NE75YgpUA?pwd=l5bk 提取码:l5bk
这篇关于基于matlab实现老照片的简单修复的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





