谷歌吹捧量子计算的里程碑到底是什么？

谷歌表示，它已经在量子计算研究方面取得了突破，称一个实验性的量子处理器可以在短短几分钟内完成计算，这将花费传统超级计算机数千年的时间。

研究人员写道，这项发现发表在科学期刊《自然》上，表明“量子加速在现实世界的系统中是可以实现的，并且不受任何隐藏的物理定律的限制”。

量子计算是一种新兴的技术，它在很大程度上加快了信息处理的速度。量子计算机距离实际应用还有很长的路要走，但有一天可能会彻底改变可能需要现有计算机多年的任务，包括寻找新药以及优化城市和交通规划。

该技术依赖于量子位或量子位，它们可以同时记录零和一的数据值（现代计算的语言）。包括Google，Microsoft，IBM和Intel在内的大型科技公司都在狂热地追求这项技术。

什么是量子计算机？

量子计算机在某些计算任务在量子处理器上的执行速度可能比在经典处理器1上的执行速度快。一个根本的挑战是构建一种能够在指数级大的计算空间中运行量子算法的高保真处理器。在这里，我们报道了使用具有可编程超导量子位的处理器的到53个量子位创建量子态，对应于维度2的计算状态空间53（约10 16）。重复实验的测量结果采样了概率分布，我们使用经典模拟对其进行了验证。我们的Sycamore处理器大约需要200秒来采样一百万个量子电路实例一百万次-我们的基准测试表明，最新型经典超级计算机的等效任务大约需要10,000年。这显着增加的速度相比，所有已知的经典算法是一个实验实现量子至上为这一特定的计算任务，预示一个备受期待的计算范例。

量子历程

在1980年代初期，理查德·费曼（Richard Feynman）提出，量子计算机将成为解决物理和化学问题的有效工具，因为用经典计算机模拟大型量子系统的成本成倍增加1。实现费曼的愿景提出了巨大的实验和理论挑战。首先，可以设计一个量子系统来在足够大的计算（希尔伯特）空间中以足够低的错误率执行计算吗？其次，我们能否提出一个对于经典计算机来说很难解决但对于量子计算机来说容易解决的问题？通过在我们的超导量子位处理器上计算这样的基准任务，我们解决了两个问题。我们的实验实现了量子至上性，这是全面量子计算之路的里程碑。

在达到这一里程碑的过程中，我们证明了量子加速在现实世界的系统中是可以实现的，并且不受任何隐藏的物理定律的限制。量子至上也预示着嘈杂的中级量子（NISQ）技术的时代15。我们演示的基准测试任务可立即应用于生成可认证的随机数（S. Aaronson，准备中的手稿）；这种新的计算能力的其它初始用途可包括优化，机器学习，材料科学和化学。然而，实现量子计算的全部承诺（使用肖尔的保理算法，例如）仍然需要技术飞跃来设计容错逻辑量子位。

为了实现量子至上，我们取得了许多技术进步，也为纠错铺平了道路。我们开发了可以在二维qubit阵列上同时执行的快速，高保真门。我们使用功能强大的新工具：交叉熵基准测试11在组件和系统级别上对处理器进行了基准测试。最后，我们使用了组件级的保真度来准确地预测整个系统的性能，从而进一步证明了在扩展到大型系统时量子信息的行为符合预期。

合适的计算任务

为了证明量子至上，我们比较我们针对国家的最先进的经典计算机量子处理器中取样的伪随机量子电路的输出的任务。随机电路是用于基准测试的合适的选择，因为它们不具有的结构，因此允许计算硬度的保证限于。我们设计电路，通过重复应用单量子位和两量子位逻辑运算来纠缠一组量子位（量子位）。对量子电路的输出进行采样会生成一组位串，例如{0000101，1011100，…}。由于量子干扰，位串的概率分布类似于激光散射中光干扰产生的斑点强度图案，因此某些位串比其他位串更容易出现。传统上，随着量子位的数量（宽度）和门循环数量（深度）的增长，计算这种概率分布的难度成倍增加。

我们验证该量子处理器是否工作正常使用称为交叉熵法基准，其比较多久各比特串与通过模拟计算出的经典计算机上相应的理想概率实验观察。对于给定的电路，我们收集所测量的位串{ X 我 }，并计算线性交叉熵基准保真度（也参见  补充信息），这是我们所测量的位串的模拟概率的平均值：

其中n是量子位的数量，P（x i）是为理想量子电路计算的位串x i的概率，并且平均值在观察到的位串上。凭直觉FX Ë 乙与我们采样高概率位串的频率相关。当量子电路中没有错误时，概率分布是指数分布（请参见补充信息），并且从该分布中采样将产生FX Ë 乙= 1。在另一方面，从均匀分布采样会给〈 P（X 我）〉 我  = 1/2 Ñ和产生FX Ë 乙= 0。的价值FX Ë 乙在0和1之间的值对应于电路运行时未发生错误的可能性。概率P（x i）必须通过经典地模拟量子电路并由此计算得出FX Ë 乙在量子至上的体制中是棘手的。但是，通过某些简化的电路，我们可以获得运行宽和深量子电路的完全运行处理器的定量保真度估计。

我们的目标是达到足够高的水平 FX Ë 乙对于具有足够宽度和深度的电路来说，传统的计算成本非常高。这是一项艰巨的任务，因为我们的逻辑门不完善，并且我们打算创建的量子态对错误敏感。在算法过程中的单个位或相位翻转将完全打乱散斑图样，并导致逼真度接近于零11（另请参见  补充信息）。因此，为了主张量子优势，我们需要一个量子处理器，该处理器以足够低的错误率执行程序。

构建高保真处理器

我们设计了一个名为“ Sycamore”的量子处理器，它由54个transmon量子位的二维阵列组成，其中每个量子位可调谐地耦合到一个矩形格子中的四个最近的邻居。该连接被选择为使用表面代码26与纠错具有前向兼容性。该器件的一项关键系统工程进展是，不仅可以孤立地实现高保真单量子比特和两个量子比特的运算，而且还可以在许多量子比特上同时进行门运算的同时进行现实的计算。我们在下面讨论重点内容；另请参阅  补充信息。

在一个超导电路，传导电子冷凝成宏观量子状态，使得电流和电压表现量子机械2，30。我们的处理器使用transmon量子位6，可以将其视为5-7 GHz的非线性超导谐振器。量子位被编码为谐振电路的两个最低量子本征态。每个transmon都有两个控件：一个微波驱动器来激发qubit，以及一个磁通量控制器来调谐频率。每个量子位连接到用于读出量子位状态5的线性谐振器。如示于图1中，每个量子位被使用新的可调耦合器也连接到其相邻的量子位31，32。我们的耦合器设计使我们能够快速将qubit-qubit耦合从完全关断调整到40 MHz。1个量子位无法正常运行，因此该设备使用53个量子位和86个耦合器。

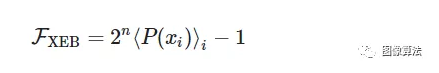
a，处理器的布局，显示了一个54个量子位的矩形阵列（灰色），每个矩形都通过耦合器（蓝色）连接到其四个最近的邻居。概述了不可操作的量子位。b，美国梧桐芯片的照片。

该处理器使用铝制造，以实现金属化和约瑟夫森结，并使用铟制造两个硅晶片之间的凸点。芯片被引线键合到超导电路板上，并在稀释冰箱中冷却至20 mK以下，以将环境热能降低到大大低于量子位能。处理器通过滤波器和衰减器连接到室温电子设备，后者可合成控制信号。所有量子位的状态可以通过同时利用频率复用的技术来读取33，34。我们使用两级低温放大器来增强信号，该信号被数字化（在1 GHz时为8位）并在室温下以数字方式多路分解。我们总共精心设计了277个数模转换器（在1 GHz时为14位），以完全控制量子处理器。

我们通过驱动25ns的微波脉冲来执行单量子位门控，该微波脉冲会以qubit频率谐振，同时关闭qubit-qubit耦合。脉冲被成形为最小化到较高的transmon状态35的过渡。门性能由于两电平系统的缺陷频率强烈变化36，37，杂散微波模式，耦合到控制线和读出谐振器中，量子位，磁通噪声和脉冲畸变之间残留的杂散耦合。因此，我们优化了单量子位操作频率以减轻这些错误机制。

我们通过使用上述交叉熵基准测试协议（降低到单量子位级别（n  = 1））对单量子位门性能进行基准测试，以测量在单量子位门限期间发生错误的可能性。在每个量子位上，我们应用随机选择的门的可变数量m并进行测量FX Ë 乙在许多序列上取平均值；随着m的增加，误差累积并平均FX Ë 乙衰变。我们用[1 − e 1 /（1 − 1 / D 2）] m对此衰减建模  ，其中e 1是Pauli误差概率。在这种情况下，状态（希尔伯特）空间维数D  = 2 n等于2，它校正了带有误差部分与理想状态重叠的去极化模型。这个过程类似于随机的基准的较典型的技术27，38，39，但支持非克利福栅设置40并可以从相干控制误差中分离出相干误差。然后，我们重复所有实验同时执行单量子位门的实验（图2），这表明错误概率仅小幅增加，表明我们的设备具有较低的微波串扰。

a，对孤立的量子位（虚线）和同时操作所有量子位（实线）时测得的泡利误差（黑色，绿色，蓝色）和读出误差（橙色）的积分直方图（经验累积分布函数，ECDF）。每个分布的中值出现在垂直轴上的0.50处。平均值（平均值）如下所示。b，热图，显示了位于处理器布局中的单量子比特和两比特泡利误差e 1（十字）和e 2（条）。显示了同时运行的所有量子位的值。

我们通过使相邻的量子位共振并打开20 MHz耦合12 ns来执行类iSWAP的两个量子纠缠门，从而允许量子位交换激励。在这段时间内，量子位还经历了受控相位（CZ）交互作用，该交互作用来自于更高的Transmon级别。优化每对量子位的两个量子位门限频率轨迹，以减轻在优化单量子位工作频率时所考虑的相同误差机制。

为了表征和量化两个量子位门，我们运行了m个周期的两个量子位电路，其中每个周期在两个量子位的每一个上都包含一个随机选择的单量子位门，然后是固定的两个量子位门。我们通过使用来学习二量子位ary的参数（例如iSWAP和CZ交互的数量）FX Ë 乙作为成本函数。经过优化后，我们从的衰减中提取出每个周期的误差e 2 c。FX Ë 乙与m并通过减去两个单量子位误差e 1来隔离两个量子位误差e 2。我们发现平均e 2为0.36％。另外，我们在重复执行相同的过程的同时为整个阵列运行两个量子比特的电路。在更新单位参数以解决诸如色散漂移和串扰等影响后，我们发现平均e 2为0.62％。

对于整个实验，我们使用在同时操作期间为每对测量的两个量子比特unit生成量子电路，而不是为所有对使用标准门。典型的两个量子比特的门是一个完整的iSWAP，具有完整CZ的1/6。绝不使用单独校准的门限制演示的通用性。例如，一个人可以由1个量子比特的门和任意给定对中的两个唯一的2个量子比特的门组成可控NOT（CNOT）门。本地实施高保真“教科书门”，例如CZ或我š W¯¯ 甲P------√，正在进行中。

最后，我们使用标准色散测量41来对量子位读数进行基准测试。在图2a中示出了在0和1状态上平均的测量误差。我们还通过随机准备每个处于0或1状态的量子位，然后测量所有量子位以获得正确结果的概率，来同时测量所有量子位时的误差。我们发现，同时读出仅导致每量子位测量误差的适度增加。

找到各个门和读出的错误率后，我们可以将量子电路的保真度建模为所有门和测量的无错误操作概率的乘积。我们最大的随机量子电路具有53个量子比特，1,113个单量子比特门，430个两个量子比特门，以及每个量子比特的测量值，我们预测它们的总保真度为0.2％。保真度应该可以通过几百万次测量来解决，因为FX Ë 乙 是 1 / Ns--√，其中N s是样本数。我们的模型假设，纠缠越来越大的系统不会引入超出我们在单比特和两比特级别上测量的误差之外的其他误差源。在下一节中，我们将了解该假设的成立情况。

至高无上制度下的逼真度估计

我们的伪随机量子电路生成的门序列如图3所示。该算法的一个周期包括应用从中随机选择的单量子位门{ X--√，Y--√，W--√}在所有量子位上，然后是成对的量子位上的两个量子门。形成“至上电路”的门序列被设计为最小化创建高度纠缠态所需的电路深度，这是计算复杂性和经典硬度所必需的。

a，我们实验中使用的示例量子电路实例。每个周期包括一个单比特和两个量子比特门的层。单量子位门是从以下位置随机选择的{ X--√，Y--√，W--√}，在哪里  w ^= （X+ Y）/ 2–√门不会顺序重复。根据平铺模式选择两个qubit门的顺序，将每个qubit顺序耦合到其四个最邻近的qubit。耦合器分为四个子集（ABCD），每个子集在与阴影颜色相对应的整个阵列中同时执行。在这里，我们显示了一个棘手的序列（重复ABCDCDAB）；我们还使用了不同的耦合器子集以及可在经典计算机上模拟的可简化序列（重复EFGHEFGH，未显示）。b，单量子比特和二量子比特门的控制信号的波形。

虽然我们无法计算 FX Ë 乙在至高无上的体系中，我们可以使用三种变化来估计它，以降低电路的复杂性。在“补丁电路”中，我们删除了两个量子比特门的一部分（占两个量子比特门总数的一小部分），将电路划分为两个空间隔离的，互不影响的量子比特补丁。然后，我们将总保真度计算为补丁保真度的乘积，可以轻松计算出每个保真度。在“消除电路”中，我们仅沿切片去除了一部分初始的两个量子比特门，从而允许了补丁之间的纠缠，这更紧密地模仿了整个实验，同时仍然保持了仿真的可行性。最后，我们还可以运行完整的“验证电路”，其门数与我们的至高无上的电路相同，但对两个量子比特门的序列具有不同的模式， 补充信息）。这三种变化之间的比较使我们能够在接近至上制度时追踪系统的保真度。

我们首先检查验证电路的补丁版本和删减版本是否与完整验证电路产生相同的保真度，最高可达53 qubit，如图4a所示。对于每个数据点，我们通常在十个电路实例中收集N s = 5×10 6个样本，其中实例仅在每个周期的单量子位门选择上有所不同。我们还显示了预测FX Ë 乙通过将单量子比特门和两个量子比特门的无误概率与测量值相乘得出的值（另请参见  补充信息）。尽管计算复杂度和纠缠度存在巨大差异，但预测的，补丁的和消除的保真度均与相应完整电路的保真度显示出良好的一致性。这使我们充满信心，可以使用消隐电路来准确估计更为复杂的电路的保真度。

a，基准测试方法的验证。FX Ë 乙根据测得的位串和经典模拟预测的相应概率，计算出补丁，消除和完整验证电路的值。在此，以可简化的平铺和顺序方式应用两个量子位的门，以便可以在合理的时间内将整个电路模拟为n = 53，m = 14。每个数据点是十个不同量子电路实例的平均值，这些实例的单量子位门有所不同（对于n = 39、42和43，仅模拟了两个实例）。对于每个n，每个实例的N s为0.5-250万。黑线显示预测的FX Ë 乙基于单量子比特和二量子比特的门和测量误差。尽管它们在复杂性方面存在巨大差异，但所有四个曲线之间的紧密对应关系证明，可以使用消隐电路来估计至高无上的状态下的逼真度。b，估计FX Ë 乙在量子至上制度中。在这里，两个量子比特的门以不可简化的平铺和顺序应用，因此很难模拟。对于最大的消减数据（n = 53，m = 20，总N s = 3000万），我们找到了一个平均值FX Ë 乙 > 0.1％，具有5个σ置信度，其中σ包括系统和统计上的不确定性。预计未模拟但已存档的相应全电路数据将显示类似的统计上显着的保真度。对于m = 20，在量子处理器上获得一百万个样本需要200秒，而在一百万个内核上进行等保真度经典采样将花费10,000年，而对保真度的验证将花费数百万年。

仍可直接验证保真度的最大电路具有53量子比特和简化的门电路。以0.8％的保真度对它们执行随机电路采样需要130万个内核，耗时130秒，相当于量子处理器相对于单个内核的百万倍加速。

现在，我们开始对计算上最困难的电路进行基准测试，这只是对两个量子位门的重新布置。在图4b中，我们显示了FX Ë 乙用于深度不断增加的53比特补丁和全至尊电路的隐蔽版本。对于具有53个量子比特和20个周期的最大电路，我们在十个电路实例中收集了N s  = 30×10 6个样本，得出FX Ë 乙= （2.24 ± 0.21 ）× 10− 3用于消隐电路。以5σ置信度，我们断言在量子处理器上运行这些电路的平均保真度至少大于0.1％。我们期望图4b的完整数据应具有相似的保真度，但是由于仿真时间（红色数字）需要很长时间才能检查，因此我们已将数据存档（请参见“数据可用性”部分）。因此，数据处于量子至上状态。

经典计算成本

我们在经典计算机上模拟实验中使用的量子电路，有两个目的：（1）通过计算验证我们的量子处理器和基准测试方法 FX Ë 乙在可能的情况下使用可简化的电路（图4a），以及（2）估算FX Ë 乙以及采样最困难电路的经典成本（图4b）。多达43个量子位，我们使用Schrödinger算法，该算法模拟了完整量子态的演化。Jülich超级计算机（具有100,000个内核，250 TB）运行情况最大。超过此大小，没有足够的随机存取存储器（RAM）来存储量子状态42。对于更大的量子比特数，我们使用混合Schrödinger–Feynman算法43在Google数据中心上运行以计算单个位串的幅度。该算法将电路分解为两个量子位补丁，并使用Schrödinger方法有效地模拟每个补丁，然后再使用一种类似于费曼路径积分的方法将它们连接起来。尽管具有更高的内存效率，但随着路径深度与连接补丁的门的数量呈指数增长，随着电路深度的增加，Schrödinger-Feynman算法的计算量也成倍增加。

为了估算至上电路的经典计算成本（图4b中的灰色数字），我们在Summit超级计算机以及Google集群上运行了部分量子电路仿真，并推断出全部成本。在此推断中，我们通过按比例缩放验证成本来考虑采样的计算成本FX Ë ，0.1％的保真度降低了约1000的成本。上峰会超级计算机，这是目前世界上最强大的，我们使用由Feynman路径-积分是最有效的在低深度启发的方法。在m  = 20时，张量无法合理地放入节点内存中，因此我们只能测量直到m  = 14的运行时，为此我们估计，采样1％保真度的300万个位串将需要一年。

在Google Cloud服务器上，我们估计 使用Schrödinger–Feynman算法以0.1％的保真度在m = 20时执行相同的任务将耗费50万亿个核心小时，并消耗1皮瓦小时的能源。从角度来看，对量子处理器上的电路进行三百万次采样需要600秒，而采样时间受到控制硬件通信的限制；实际上，净量子处理器时间仅为30秒左右。来自所有电路的位串样本已在线存档（请参见“数据可用性”部分），以鼓励开发和测试更高级的验证算法。

有人可能想知道算法创新可以在多大程度上增强经典模拟效果。我们假设的基础上，从复杂性理论的见解，是这个算法任务的成本是电路尺寸指数。实际上，模拟方法在过去几年中稳步提高。我们预计最终将实现比此处报告的更低的仿真成本，但我们也希望大型量子处理器的硬件改进将始终超过仿真成本。

验证数字错误模型

量子误差校正的理论基础的关键假设是，量子态的错误可以被认为是数字化的和局部。在这样的数字模型下，演化量子态中的所有误差都可以通过散布在电路中的一组局部保利误差（位翻转或相位翻转）来表征。由于连续幅度是量子力学的基础，因此需要测试量子系统中的错误是否可以视为离散和概率。确实，我们的实验观察结果支持该模型对处理器的有效性。我们的系统保真度可以通过一个简单的模型很好地预测，在该模型中，每个门的各个特征保真度相乘在一起（图4）。

为了由数字化误差模型成功描述，系统的相关误差应该很小。我们通过选择随机电路和去相关的错误，通过优化控制，以尽量减少系统误差和渗漏，并通过设计运行速度比相关噪声源快得多门，如1 /做到这一点在我们的实验˚F通量噪音。通过对高达的希尔伯特空间的预测性不相关误差模型进行演示，可以表明我们可以构建一个系统，在该系统中，量子资源（例如纠缠）不会非常脆弱。

未来

基于超导量子位的量子处理器现在可以在2维的希尔伯特空间执行计算53  ≈9×10 15，超越最快古典超级计算机的范围今天可用。据我们所知，该实验标志着只能在量子处理器上执行的第一个计算。因此，量子处理器已达到量子至上的状态。我们预计，他们的计算能力将继续以双指数率增长：与计算量成倍模拟量子电路增加的成本古典和硬件的改善可能会遵循量子处理器相当于摩尔定律的，每隔几年将此计算量增加一倍。为了维持双指数的增长速度，并最终提供运行众所周知量子算法，如绍尔所需的计算量或格罗弗算法25，54，量子纠错的工程将需要成为大家关注的焦点。

Bernstein和Vazirani 55提出的扩展的Church-Turing论文断言，任何“合理”的计算模型都可以由Turing机有效地模拟。我们的实验表明，现在可以使用一种违反此主张的计算模型。我们已经使用物理上可实现的量子处理器（具有足够低的错误率）在多项式时间内执行了随机量子电路采样，但是对于经典的计算机器，尚不存在有效的方法。这些发展的结果是，量子计算正在从研究主题过渡到释放新计算能力的技术。我们只是远离有价值的近期应用程序的一种创新算法。

超多论文源码下载地址：关注“图像算法”微信公众号