本文主要是介绍写给学生看的系统分析与验证笔记(十)——Büchi自动机(Büchi automata),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
- 正则表达式
- ω-正则表达式(ω-regular expression)
- ω-正则属性
- 非确定性Büchi自动机(NBA)
- ω-正则属性与Büchi自动机的联系
由上一节中,我们将NFA用于正则安全性的验证,但是有很大一部分线性属性不属于正则属性,现在我们要验证非正则的属性,采取的方法也是类似的,要将非正则属性转换为一种自动机,为此我们需要一种新的自动机,它就是Büchi自动机
正则表达式
首先回顾一下正则表达式
正则表达式的定义为
E : : = ∅ | ε | A | E+E’ | E.E’ | E* E ::= \varnothing\text{ | ε | A | E+E' | E.E' | E*} E::=∅ | ε | A | E+E’ | E.E’ | E*
正则表达式描述的是有限字的语言,它的语义表示为:
E ↦ L ( E ) ⊆ Σ ∗ E \mapsto L(E)\subseteqΣ^* E↦L(E)⊆Σ∗
↦ \mapsto ↦这个符号的意思是maps to
我们有如下规则
L ( ∅ ) = ∅ L ( ε ) = { ε } L ( A ) = { A } L(\varnothing)=\varnothing\; L(ε)=\{ε\}\; L(A)=\{A\} L(∅)=∅L(ε)={ε}L(A)={A}
L ( E 1 + E 2 ) = L ( E 1 ) ∪ L ( E 2 ) 并 ( u n i o n ) L(E_{1}+E_{2})=L(E_{1})\cup L(E_{2})\; 并(union) L(E1+E2)=L(E1)∪L(E2)并(union)
L ( E 1 ⋅ E 2 ) = L ( E 1 ) L ( E 2 ) 级 联 ( c o n c a t e n a t i o n ) L(E_{1}·E_{2})=L(E_{1})L(E_{2})\; 级联(concatenation) L(E1⋅E2)=L(E1)L(E2)级联(concatenation)
L ( E ∗ ) = L ( E ) ∗ 克 林 闭 包 ( kleene closure ) L(E^*)=L(E)^* \;克林闭包(\text{kleene closure}) L(E∗)=L(E)∗克林闭包(kleene closure)
ω-正则表达式(ω-regular expression)
ω-正则表达式就是在正则表达式的基础上加入了ω运算
ω-regular expression=regular expression+ω operation a ω \text{ω-regular expression=regular expression+ω operation }a^{ω} ω-regular expression=regular expression+ω operation aω
ω和*操作不同,*表示的是有限次重复,例如a*=aaa…a,而ω代表的是无限次重复, a ω = a a a . . . a^ω=aaa... aω=aaa...
如果L语言上带了ω,则表示的是它是一个无限字的集合,记为
L ω = { w 1 w 2 w 3 . . . ∣ 对 所 有 i ≥ 1 来 说 w i ∈ L } L^ω=\{w_{1}w_{2}w_{3}...|对所有i\ge1来说w_{i}∈L\} Lω={w1w2w3...∣对所有i≥1来说wi∈L}
ω-正则表达式的语法(syntax)表示为:
γ = α 1 ⋅ β 1 ω + . . . + α n ⋅ β n ω \gamma=\alpha_{1}·\beta_{1}^ω+...+\alpha_{n}·\beta_{n}^ω γ=α1⋅β1ω+...+αn⋅βnω
α i , β i \alpha_{i},\beta_{i} αi,βi是字母表Σ上的正则表达式
ω-正则表达式的语义(semantics)的含义是语法 γ \gamma γ生成的语言,表示为:
L ω = ⋃ 1 ≤ i ≤ n L ( α i ) L ( β i ) ω L_{ω}=\bigcup\limits_{1\le i\le n}L(\alpha_{i})L(\beta_{i})^ω Lω=1≤i≤n⋃L(αi)L(βi)ω
由ω-正则表达式生成的语言称为ω-正则语言,记为 L = L ω ( γ ) L=L_{ω}(\gamma) L=Lω(γ)
例如ω-正则表达式 ( A ∗ . B ) ω (A^*.B)^ω (A∗.B)ω,它生成的语言包含的字可以是BBBB…,BABAABAAAB…。
例题:请提供对应的ω-正则表达式,设Σ={A,B}
-
在Σ上无限字的集合,包含有限多个A
( A + B ) ∗ . B ω (A+B)^*.B^ω (A+B)∗.Bω -
在Σ上无限字的集合,每个A后面都会出现B
( B ∗ . A . B ) ∗ . B ω + ( B ∗ . A . B ) ω (B^*.A.B)^*.B^ω+(B^*.A.B)^ω (B∗.A.B)∗.Bω+(B∗.A.B)ω
这里的两个式子分别考虑了A出现有限次和无限次的情况 -
在Σ上无限字的集合,A后面最终会出现B(就是允许出现多个A然后跟着B)
( B ∗ . A + . B ) ∗ . B ω + ( B ∗ . A + . B ) ω (B^*.A^+.B)^*.B^ω+(B^*.A^+.B)^ω (B∗.A+.B)∗.Bω+(B∗.A+.B)ω
几乎是同样的式子,不过这里的A允许出现多个,所以用了+,表示出现一次或一次以上, A + = A . A ∗ A^+=A.A^* A+=A.A∗
ω-正则属性
属性P如果被称为ω-正则属性,当且仅当存在一个在AP上的ω-正则表达式 γ \gamma γ使 P = L ω ( γ ) P=L_{ω}(\gamma) P=Lω(γ)
对比一下前面的正则安全性,ω-正则属性要求P是一个ω-正则语言,而正则安全性则需要借助坏前缀,要求BadPref( P s a f e P_{safe} Psafe)是一个正则语言
例如,AP={A,B},现在有一个不变性,它的不变条件为 Φ = a ∨ ¬ b \Phi=a\vee \lnot b Φ=a∨¬b,那么我们可以构建一个ω-正则表达式,使得它生成的语言满足不变性
( ∅ + { a } + { a , b } ) ω (\varnothing+\{a\}+\{a,b\})^ω (∅+{a}+{a,b})ω
∅ \varnothing ∅相当于 ¬ a ∧ ¬ b \lnot a\wedge\lnot b ¬a∧¬b,代入 Φ \Phi Φ的结果为真,{a}和{a,b}代入也是同理,它生成的语言类似于 ∅ ∅ { a } { a , b } . . . \varnothing\varnothing\{a\}\{a,b\}... ∅∅{a}{a,b}...这样的无限字集合
我们也可以用符号来表示这个不变属性
( a ∨ ¬ b ) ω = ( ∅ + { a } + { a , b } ) ω (a\vee \lnot b)^ω=(\varnothing+\{a\}+\{a,b\})^ω (a∨¬b)ω=(∅+{a}+{a,b})ω
从这里例子中我们可以推广出一般性的结论
每个不变性都是ω-正则的
Φ \Phi Φ为不变条件,然后构建出一个满足 Φ \Phi Φ成立的条件集合:
{ A ⊆ A P : A ⊨ Φ } = { A 1 . A 2 , . . . A k } \{A\subseteq AP:A\vDash\Phi\}=\{A_{1}.A_{2},...A_{k}\} {A⊆AP:A⊨Φ}={A1.A2,...Ak}
那么使得不变性"always Φ \Phi Φ"满足的ω-正则表达式为:
( A 1 + . . . + A k ) ω (A_{1}+...+A_{k})^ω (A1+...+Ak)ω
再来看一些其他的例子
-
无限经常次a成立
( ( ¬ a ) ∗ . a ) ω = ( ( ∅ + { b } ) ∗ . ( { a } + { a , b } ) ) ω ((\lnot a)^*.a)^ω=((\varnothing+\{b\})^*.(\{a\}+\{a,b\}))^ω ((¬a)∗.a)ω=((∅+{b})∗.({a}+{a,b}))ω -
最终a会成立(LTL表示为 ◊ a \Diamond a ◊a)
t r u e ∗ a ω t r u e ω = ( 2 A P ) ∗ . ( { a } + { a , b } ) . ( 2 A P ) ω true^*a^ωtrue^ω=(2^{AP})^*.(\{a\}+\{a,b\}).(2^{AP})^ω true∗aωtrueω=(2AP)∗.({a}+{a,b}).(2AP)ω -
最终a总是成立(用LTL表示为 ◊ □ a \Diamond\Box a ◊□a)
t r u e ∗ a ω = ( 2 A P ) ∗ . ( { a } + { a , b } ) true^*a^ω=(2^{AP})^*.(\{a\}+\{a,b\}) true∗aω=(2AP)∗.({a}+{a,b})
非确定性Büchi自动机(NBA)
在前面我们知道非确定性的有限自动机可以接受正则语言,同样的,我们也需要一种自动机可以接受ω-正则语言,这种自动机就是Nondeterministic Büchi Automaton
NBA由一个五元组 ( Q , Σ , q 0 , F , δ ) (Q,Σ,q_{0},F,δ) (Q,Σ,q0,F,δ)构成:
- Q Q Q是一组状态的集合
- Σ Σ Σ是输入字母表
- q 0 q_{0} q0是初始状态
- F F F是终止状态的集合
- δ δ δ是转换函数: Q × Σ → 2 Q Q×Σ\rightarrow 2^Q Q×Σ→2Q
这个定义和NFA是一样的,没什么特别的,NFA接受的是有限字,而NBA接受的是无限字
如果自动机输入一个无限字 w o r d = A 0 A 1 A 2 . . . word=A_{0}A_{1}A_{2}... word=A0A1A2...,那么自动机的运行(run)序列可以表示为 π = q 0 q 1 q 2 . . . \pi=q_{0}q_{1}q_{2}... π=q0q1q2...,如果 π \pi π是可以被NBA接受的,那么
∃ ∞ i , q i ∈ F \overset{∞}\exist i,q_{i}∈F ∃∞i,qi∈F
就是说能够被接受的无限字可以使NBA无限经常次访问终止状态
NBA的可接受语言表示为:
L ω ( A ) = { σ ∈ Σ ω ∣ 无 限 字 σ 输 入 自 动 机 存 在 一 条 可 接 受 的 运 行 } L_{ω}(A)=\{\sigma∈Σ^ω|无限字\sigma输入自动机存在一条可接受的运行\} Lω(A)={σ∈Σω∣无限字σ输入自动机存在一条可接受的运行}
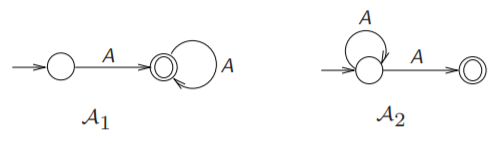
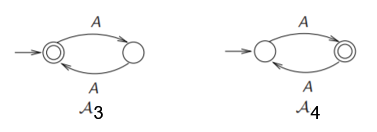
下面有四个状态机,在它们分别为NFA和NBA的情况下,看看它们所接受的语言是什么
| - | NFA | NBA |
|---|---|---|
| A1 | L ( A 1 ) = { A n + 1 ∣ n ∈ N } L(A_{1})=\{A^{n+1} \mid n∈N\} L(A1)={An+1∣n∈N} | L ω ( A 1 ) = { A ω } L_{ω}(A_{1})=\{A^ω\} Lω(A1)={Aω} |
| A2 | L ( A 2 ) = { A n + 1 ∣ n ∈ N } L(A_{2})=\{A^{n+1} \mid n∈N\} L(A2)={An+1∣n∈N} | L ω ( A 2 ) = ∅ L_{ω}(A_{2})=\varnothing Lω(A2)=∅ |
| A3 | L ( A 3 ) = { A 2 n + 1 ∣ n ∈ N } L(A_{3})=\{A^{2n+1} \mid n∈N\} L(A3)={A2n+1∣n∈N} | L ω ( A 3 ) = { A ω } L_{ω}(A_{3})=\{A^ω\} Lω(A3)={Aω} |
| A4 | L ( A 4 ) = { A 2 n ∣ n ∈ N } L(A_{4})=\{A^{2n} \mid n∈N\} L(A4)={A2n∣n∈N} | L ω ( A 4 ) = { A ω } L_{ω}(A_{4})=\{A^ω\} Lω(A4)={Aω} |
解释:
- 先看A1和A2,对于当这两个自动机是NFA的时候,它们是等价的,因为所接受的语言是相同的,但是当它们是NBA的时候,所接受的语言并不相等,同理,A3和A4上的NBA是等价的,而NFA不等价
- 看到A2上NBA的接受语言为空,因为没有语言能够使A2满足无限经常次访问终止状态的要求,所以就是空
ω-正则属性与Büchi自动机的联系
现在我们知道ω-正则属性,也知道了Büchi自动机,现在我们有一个结论
P 是 一 个 L T 属 性 , 如 果 P 是 ω − 正 则 属 性 , 当 且 存 在 非 确 定 性 B u ¨ c h i 自 动 机 A , 使 得 P = L ω ( A ) P是一个LT属性,如果P是ω-正则属性,当且存在非确定性Büchi自动机A,使得P=L_{ω}(A) P是一个LT属性,如果P是ω−正则属性,当且存在非确定性Bu¨chi自动机A,使得P=Lω(A)
这篇关于写给学生看的系统分析与验证笔记(十)——Büchi自动机(Büchi automata)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






