记录学习LTL2BA和SPIN实现LTL satisfiability checking

这里记录一下学习LTL2BA和SPIN实现LTL satisfiability checking

1. LTL satisfiability checking关注这样一类问题：对于一个系统，给定一个由线性时序逻辑（LTL）描述的性质，判断系统是否具有该性质，解决该问题的理论方法之一简单理解是将LTL性质转换为等价的Buchi自动机，再列举系统所有的运行轨迹，检验这些运行轨迹能否使得Buchi自动机最终停留在“接受”的状态。

2. 实现LTL satisfiability checking的方法/工具有很多，读者可以参考下面这篇文章做出的总结：

Rozier, K. Y., & Vardi, M. Y. (2007, July). LTL satisfiability checking. In International SPIN Workshop on Model Checking of Software (pp. 149-167). Springer, Berlin, Heidelberg.

3. 本文主要介绍一下以SPIN为工具的LTL satisfiability checking，

• 输入：Promela（PROcess MEta LAnguage，一种用于建模并行程序的语言），一个用于LTL satisfiability checking的Promela（.pml）文件包含两部分，分别是对于待验证系统的描述，和对于待验证性质的描述
• 输出：系统是否满足给定的性质，如果不满足则会连带输出一条系统不满足该性质的运行轨迹
• 对于性质的定义，SPIN可以接受LTL性质（其会将输入的LTL性质转换为Buchi自动机），也可以直接接受Buchi自动机（以“never claims”的形式进行定义）；另外一种输入方法是先使用特定工具将LTL性质转换为Buchi自动机，再将转换结果输入SPIN，这些工具包括LTL2AUT，LTL2BA，LTL2Buchi（JavaPathFinder）等。

本文学习使用的是LTL2BA+SPIN的组合

4. LTL2BA

官网为http://www.lsv.fr/~gastin/ltl2ba/index.php，其提供了一个在线的demo，LTL2BA的理论文章以及LTL2BA的下载。

• demo的应用示例：输入LTL公式“[] ( s ->  ( X e ) )”（意为系统当前状态如果使得命题s成立，则下一个状态需使得命题e成立），以下是输出的Buchi自动机表达式和图像

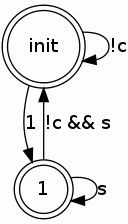
never { /* G ( c ->  ( X s ) ) */
accept_init :    /* init */if:: (!c) -> goto accept_init:: (1) -> goto accept_S2fi;
accept_S2 :    /* 1 */if:: (!c && s) -> goto accept_init:: (s) -> goto accept_S2fi;
}

• LTL2BA的下载和安装：官网上有下载连接，下载解压后需要编译c文件，作者运行系统是WIN10，采用的具体方法是下载cygwin→安装过程中勾选gcc-core和make包→将cygwin的bin目录添加至环境变量PATH→命令行在LTL2BA根目录下执行命令make -f Makefile
• 编译完成后即可命令行使用ltl2ba命令，使用方法可参见根目录下的README文档，一般使用的命令是ltl2ba -f 'formula'和ltl2ba -F xxx.txt，前者直接在命令行中输入LTL公式，后者则是将LTL公式保存在.txt文件中再运行命令
• 其它运行Makefile文件的方法可参见stackoverflow上的这个帖子How to run a makefile in Windows