LeetCode 1457. 二叉树中的伪回文路径||位运算 DFS

给你一棵二叉树，每个节点的值为 1 到 9 。我们称二叉树中的一条路径是 「伪回文」的，当它满足：路径经过的所有节点值的排列中，存在一个回文序列。

请你返回从根到叶子节点的所有路径中 伪回文 路径的数目。

示例 1：

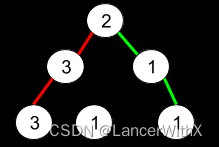
输入：root = [2,3,1,3,1,null,1]
输出：2
解释：上图为给定的二叉树。总共有 3 条从根到叶子的路径：红色路径 [2,3,3] ，绿色路径 [2,1,1] 和路径 [2,3,1] 。
在这些路径中，只有红色和绿色的路径是伪回文路径，因为红色路径 [2,3,3] 存在回文排列 [3,2,3] ，绿色路径 [2,1,1] 存在回文排列 [1,2,1] 。

示例 2：

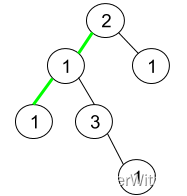
输入：root = [2,1,1,1,3,null,null,null,null,null,1]
输出：1
解释：上图为给定二叉树。总共有 3 条从根到叶子的路径：绿色路径 [2,1,1] ，路径 [2,1,3,1] 和路径 [2,1] 。
这些路径中只有绿色路径是伪回文路径，因为 [2,1,1] 存在回文排列 [1,2,1] 。

示例 3：

输入：root = [9]
输出：1

提示：

• 给定二叉树的节点数目在范围 [1, 105] 内
• 1 <= Node.val <= 9

伪回文条件：二进制表示中只有最多一个位为1（奇数次）
递归遍历树的每一个节点并记录路径，使用位运算检查是否为伪回文路径：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int pseudoPalindromicPaths(TreeNode* root) {return countPaths(root, 0);}int countPaths(TreeNode* node, int pathSta) {if (!node) {return 0;}// 使用位运算更新路径状态pathStatus ^= (1 << node->val);// 如果是叶子节点，检查路径是否是伪回文if (!node->left && !node->right) {return (pathSta & (pathSta - 1)) == 0;}// 递归计算左右子树的伪回文路径数int leftCount = countPaths(node->left, pathSta);int rightCount = countPaths(node->right, pathSta);return leftCount + rightCount;}
};

至于位运算，灵神有篇文章写得很好，读者可以看看：从集合论到位运算，常见位运算技巧分类总结！