图上作业法

目录

交通示意图的表示方法

图上作业法 

（1）对流

（2）迂回

物资调运问题的图上作业法 

交通路线不成圈

交通路线成圈 

---

交通示意图的表示方法

     交通示意图是用来表明收发点的大致位置、收发量、交通路线长度的图形。

图形表示方法：

（1）发点（产地或仓库）用符号表示，里面的数字表示发货量；

（2）收点用（需求地）用符号表示，里面的数字表示收货量；

（3）两点间的连线为交通线，其长度记在交通线旁边。

（4）物资调运的方向(流向)用符号 表示，并把按物资调运方向画在交通线的右边，把调运物资的数量记在的右边，并加上括号，以表示和交通线长度区别。

 下图是具体的物资调运交通流向图

图上作业法 

（1）对流

        即同一物资在同一线路上的往返运输。

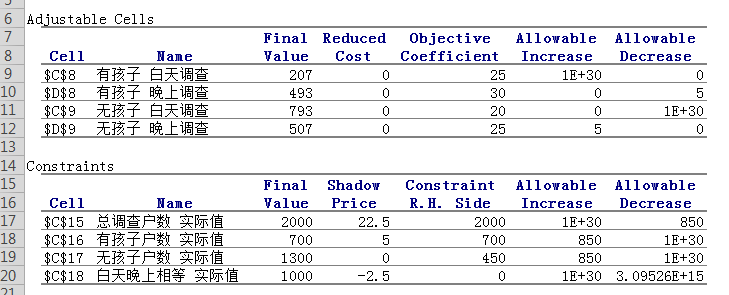
        如下面的图， 将某物资10吨，从A1运到B2，而又有同样的物资10吨，在同一期间从A2运到B1，于是A1A2间就出现了对流现象。 

运力：30*10+40*10+40*10+30*10=1400

如果从图上看，对流可以理解为同一条交通线上，有两条或两条以上的物资调运方向。 

消除对流

运力：30*10+30*10=600

（2）迂回

迂回： 在交通图成圈的时候，如果流向图中内圈流向的总长(简称内流长)或外圈流向的总长(简称外流长)超过整个圈长的一半，就称为迂回运输。

内、外圈：由于表示调运方向的箭头，要按调运方向，画在交通线的右边，因此，流向图中，有些流向就在圈外，称为外圈流向；有些流向在圈内，称为内圈流向。

  

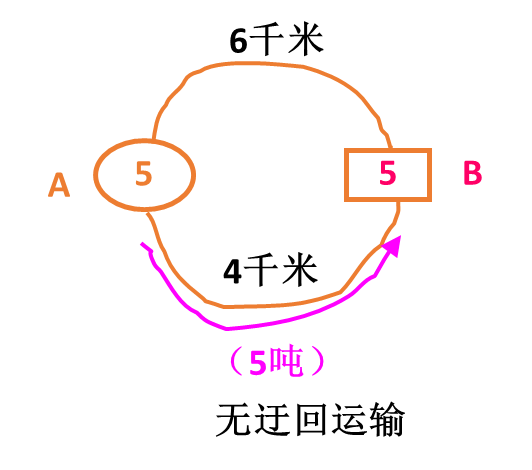
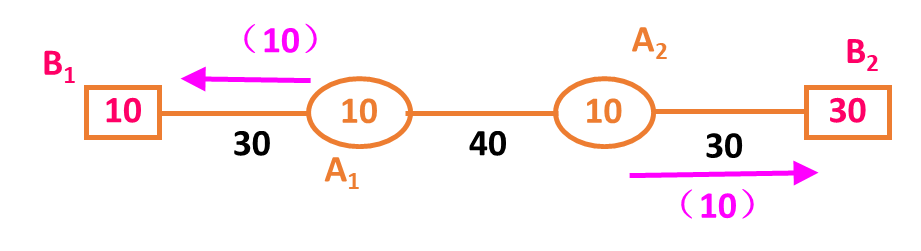
迂回运输：运力： 6*5=30吨.千米                  无迂回运输：运力：4*5=20吨.千米

例如：一交通图

发现其为迂回运输，对其进行修改

节省运力：210-200=10 

---

物资调运问题的图上作业法 

目的：消除运输过程中的对流和迂回，节省运输力量。

 在实际的物资调运中，运输线路可以分为两种情况：

交通线路成圈

交通路线不成圈

例：有某物资17万吨，由A1，A2，A3，A4发出，发量分别为5，2，3，7(万吨)，运往B1，B2，B3，B4，收量分别为8，1，3，5(万吨)，收发量平衡，交通路线如下图所示，问应如何调运，才使运输吨·千米最小？ 

解：该交通线路不成圈，只需要做一没有对流的调运图。

方法：从各端点开始，由外到里，逐步进行各收发点之间的平衡。

解法如下：

交通路线成圈 

一般步骤：

1.用破圈法编制初始方案。打破每一圈中距离最长的一段，并在交通图上，从破开的线段端点开始，标出物资流向且物资流向的箭头始终在以输出地为起点以输入地为终点的交通路线的右边。

2.检验：每一圈的内外圈长如果均不大于该圈的一半长，该方案已经最优；否则进行调整。

3.调整：找出有问题圈中的最小运量边，该圈各边减去此最小运量，该圈剩余各边加上此最小运量。（这里举个例子，①假如是内圈不符合要求，需要调整，则内圈有箭头的，其运量减去整个圈的最小运量，外圈有箭头的，其运量加上该最小运量，无箭头划着的也加上最小运量。②假如是外圈不符合要求，需要调整，则外圈有箭头的，其运量减去整个圈的最小运量，内圈有箭头的，其运量加上该最小运量，无箭头划着的也加上最小运量。）
4.重复步聚2~3，直到每一回路都达到最优。该调运方案即为最优。

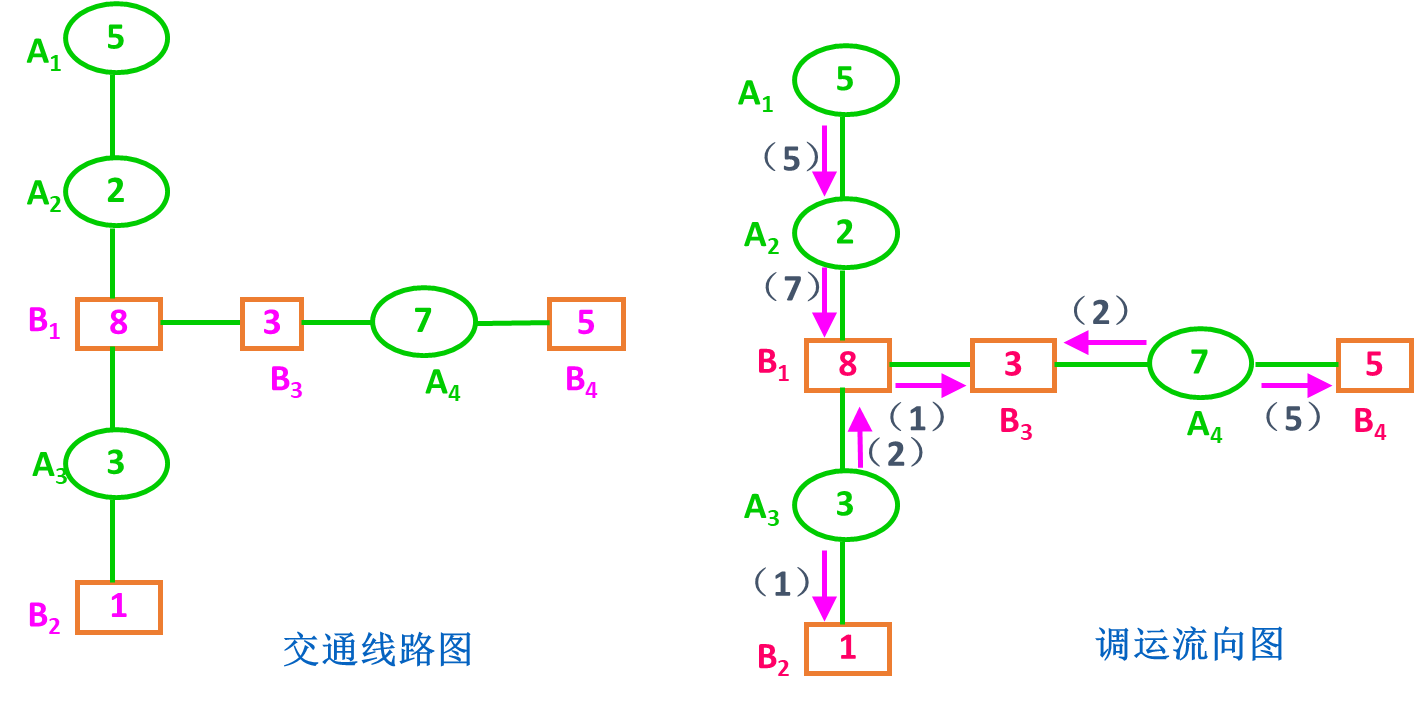
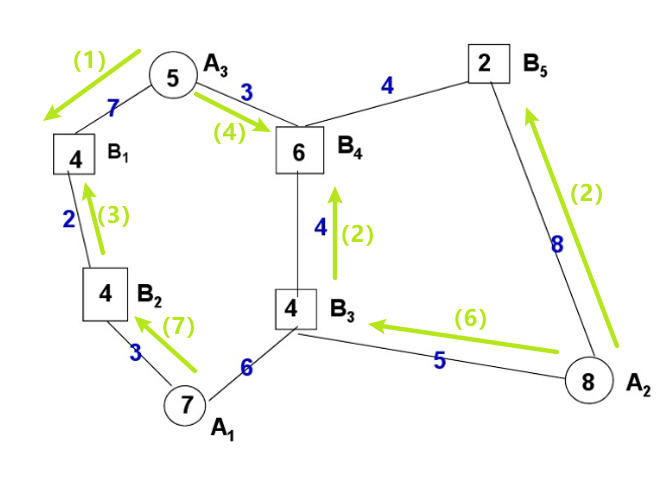
例：有某物资7万吨，由A1，A2，A3发出，发量分别为3，3，1(万吨)，运往B1，B2，B3，B4，收量分别为2，3，1，1(万吨)，收发量平衡，交通路线如下图所示，问应如何调运，才使运输吨·千米最小？

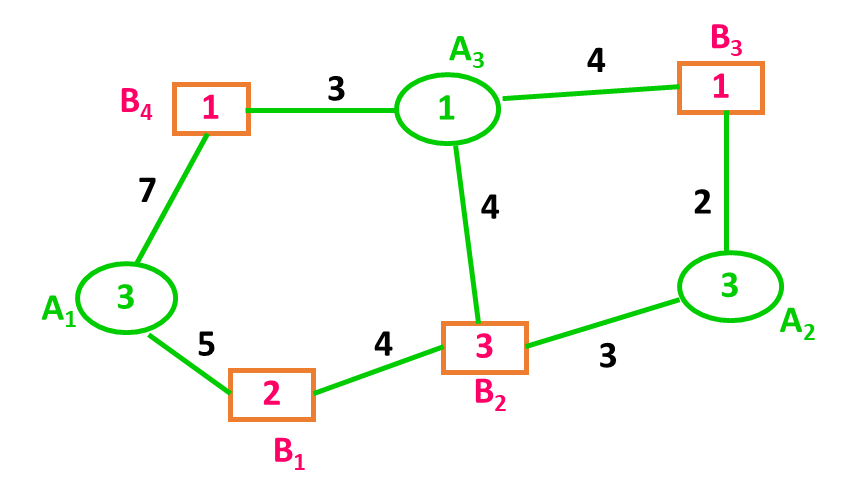
解: 

(1)作一个没有对流的流向图

  方法：用“去线破圈”的方法。去一线破一圈，有几个圈去掉几条线，把有圈的交通图，转化为不成圈的交通图。

  技巧：一般先去掉长度最长的交通线，比如本例中去掉A1B4(7千米)，破A1B1B2A3B4圈；再去掉A3B3线(4千米)，破B2A2B3A3圈。这样，原来有圈的交通图，变成了不成圈的交通图。

从各个端点开始，做一个没有对流的流向图。

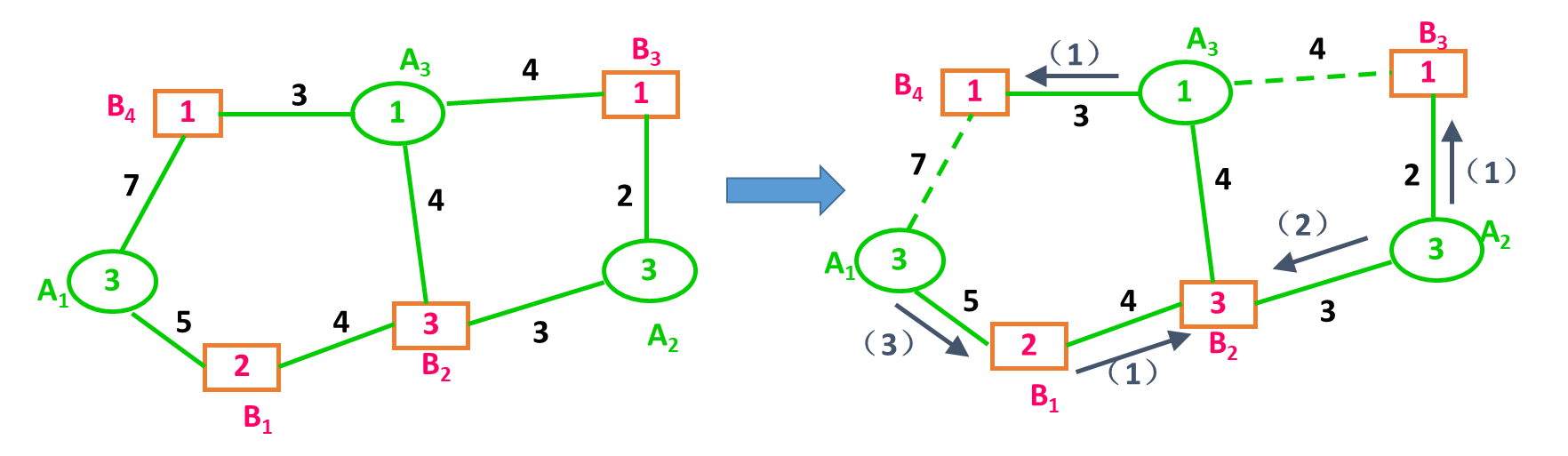(2)检查有无迂回
  方法：对流向图中的各圈进行检查，如果没有迂回，则这个初始方案就是最优方案，如果其中某圈中有迂回，则不是最优方案，需要改进。 

 

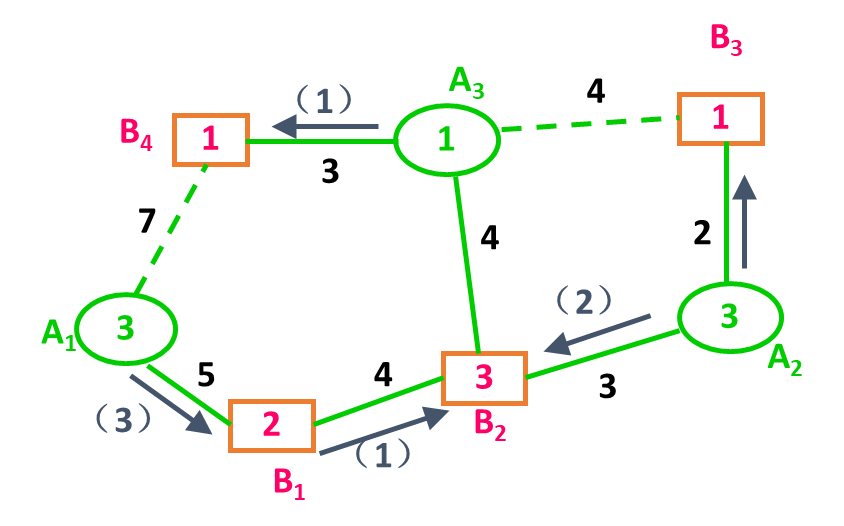
由于左边的圈中存在迂回，故需要调整 

调整方法：

1）在外圈的各流量中，减去外圈的最小流量1万吨；

2）在内圈的各流量中加上1万吨，在此圈中，因无内流量，故不加。

3）在无流量的线路上，新添加内圈流量1万吨。

得到

分析

  

因此修改后的方案为最优调运方案

总运力：1*7+2*5+1*4+2*3+1*2=29万吨·千米

大家可以试着练练

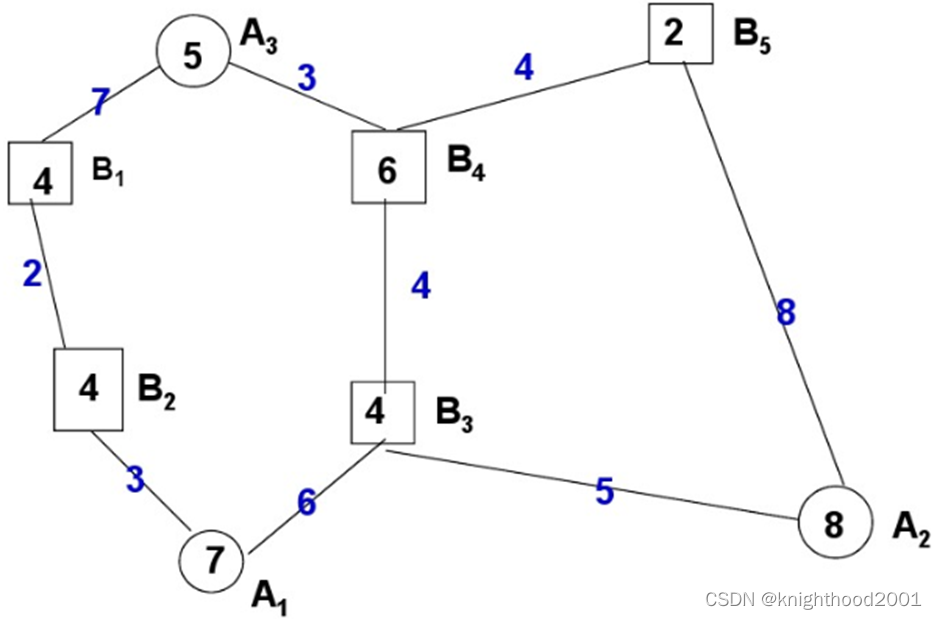
最终结果如下：