本文主要是介绍组合数学历年真题-西北工业大学-持续更新中~,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
组合数学历年考题使用说明
本文档设立的初衷是帮学弟学妹们获得一份免费且纯净的组合数学习题,把注意力和时间花在知识本身而不要浪费在筛选垃圾资料上。截止本文档创立时,学校并未提供官方习题内容,所有内容均为学长手动整理且部分为回忆版本,难免有错误、遗漏,请大家见谅。
本文档开源地址为https://gitee.com/Cheney822/nwpu-comb,转载请附原地址。欢迎广大校友积极在本仓库提交新的内容,或者修正错误。
组合数学参考资料
这里给出一些学习组合数学的参考资料:
-
课本:《组合数学》-第五版-清华大学出版社-卢华明
-
习题册:《组合数学习题解答》-第四版-清华大学出版社-卢华明
推荐刷题之前做做这本书上的题,题目范围覆盖很广,可以作为课后习题练习。
刷历年考题时遇到不会的也可以参考这本书上同类型的题。
-
PPT:(不太推荐)老师给的PPT比较老,格式和内容都有不少错误。建议听课的时候在课本上标记重难点。
-
网课:推荐清华大学马昱春老师的组合数学网课(学堂在线平台可以免费学习)
真题示例
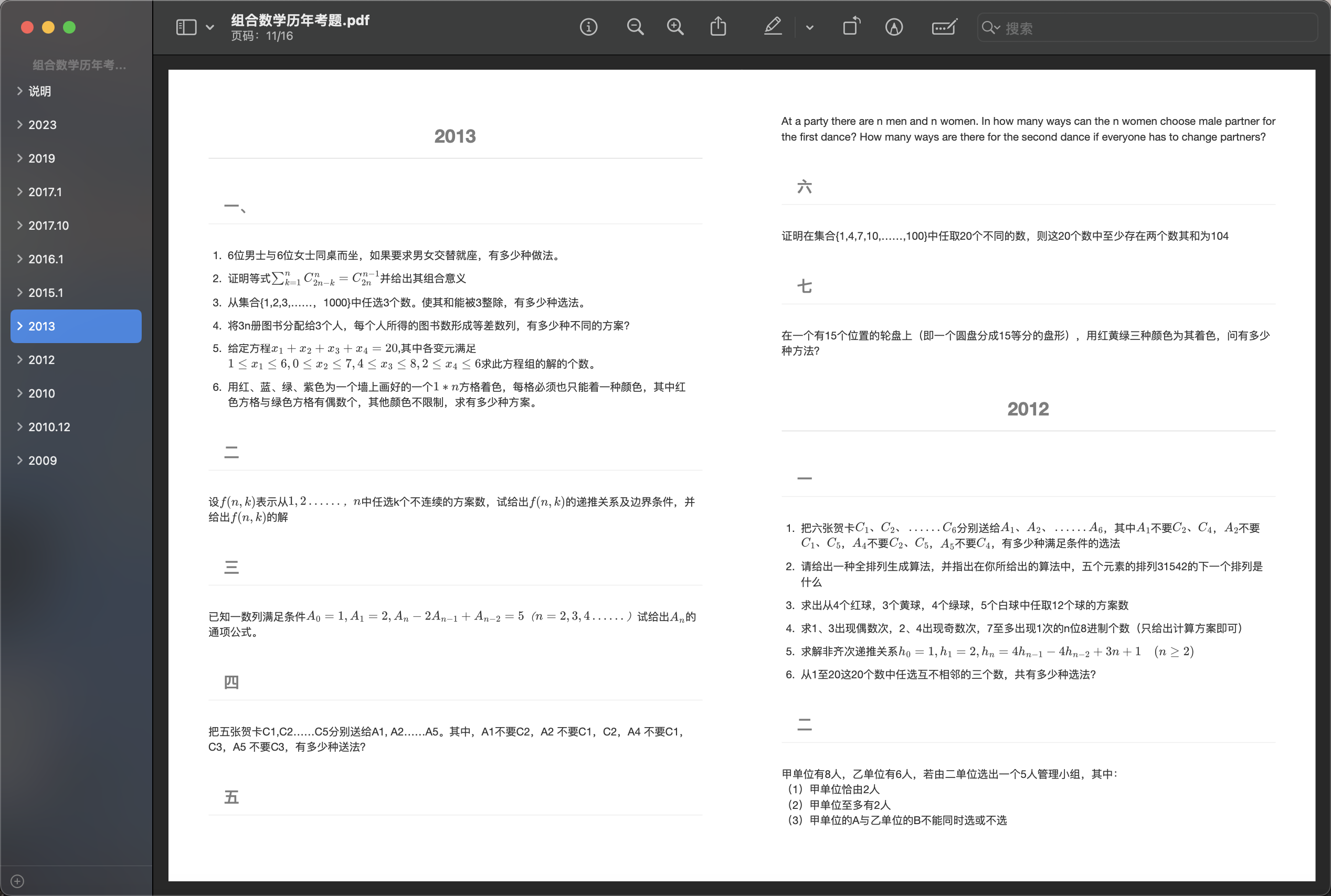
部分真题
2016.1
一、以下七个小题,每小题10分,考生可任选其中六题作答,共60分
- 在字典序法生成1-5这五个数的全排列,25431的下一个排列是什么? 若规定12345是第0号排列,54321是第 5 ! − 1 = 119 5!-1=119 5!−1=119号排列,则25431是字典序法中的第几号排列?
- 从1至20这20个数中任选互不相邻的三个数,共有多少种选法?
- 有多少个由奇数个0和奇数个3偶数个2,而1、4的个数任意的n位5进制数?
- 求不大于120素数的有多少个。
- 求从任意多个a,3个b,5个c,7个d 可重复地任取10个的方案数。
- 在一个8X8方格的国际象棋棋盘上放置一个红色、四个白色、三个黑色的八个车,保证它们不能互相攻击,问有多少种放置方法。
- 证明: ( n 2 ) ! ( n ! ) n + 1 \frac{(n^2)!}{(n!)^{n+1}} (n!)n+1(n2)!是一个整数。
二、(8分)
已知一数列满足条件: A 1 = 1 , A 2 = 2 , A n − 4 A n − 1 − 5 A n − 2 = 0 ( n = 3 , 4 , … … ) A_1=1,A_2=2,A_n-4A_{n-1}-5A_{n-2}=0 \quad(n=3,4,……) A1=1,A2=2,An−4An−1−5An−2=0(n=3,4,……),试给出 A n A_n An通项公式。
三、(10分)
把五张贺卡C1,C2……C5分别送给A1, A2……A5。其中,A1不要C2,A2 不要C1,C2,C5,A4 不要C1,C3,A5 不要C3,有多少种送法?
四、(10分)
证明:在任意的52个整数中,存在两个整数,其和或者差能被100整除。
五、第1小题4分,第2小题8分,共12分)
- 请给出六次对称群 S 6 S_6 S6的所有共轭类,并给出每一类中各有多少不同的置换。
- 用m种颜色给一个7个珠子串成的串珠着色,问有多少不同的着色方案?请再给出m=2时的具体值。
2015.1
以下11题,每题10分,可任选其中10题作答。共100分
-
在如图的6x6棋盘格内上,放置6个棋子,要求不能在同行或同列中出现两个或两个以上的棋子,且在棋盘中有“X”的地方不能放置任何棋子,请问共有多少放置方法?
X X X X X X X X X -
What is the coefficient(系数)of x 1 3 x 2 3 x 3 x 4 2 x_1^3x_2^3x_3x_4^2 x13x23x3x42 in the expansion of ( x 1 − x 2 + 2 x 3 − 2 x 4 ) 9 (x_1-x_2+2x_3-2x_4)^9 (x1−x2+2x3−2x4)9 ?
-
从1至20这20个数中任选互不相邻的三个数,共有多少种选法?
-
已知一数列满足条件:$A_0=1,A_1=2,A_n-5A_{n-1}+6A_{n-2}=2^n ,试给出 ,试给出 ,试给出A_n$通项公式。
-
设 F 1 = 1 , F 2 = 1 , F n = F n − 1 + F n − 2 ( n ≥ 3 ) F_1=1,F_2=1,F_n=F_{n-1}+F_{n-2}\quad(n\geq3) F1=1,F2=1,Fn=Fn−1+Fn−2(n≥3)证明: F 5 n F_{5n} F5n是5的倍数。
-
Find integers a,b,and c such that m 3 = a ( 3 m ) + b ( 2 m ) + c ( 1 m ) m^3=a(^m_3)+b(^m_2)+c(^m_1) m3=a(3m)+b(2m)+c(1m) for all m. Then sum the series ∑ i = 1 i 3 = 1 3 + 2 3 + 3 3 + … … + n 3 \sum_{i=1}{i^3} = 1^3+2^3+3^3+……+n^3 ∑i=1i3=13+23+33+……+n3
-
求1到1000 中不能被5、6、8整除的整数的个数。
-
证明把数A拆分成m项的拆分数,等于把n-m拆分成不多于m项的拆分数。
-
给出所有六次对称群 S 6 S_6 S6的全部共轭类,以及每个类中含有的不同置换的个数。
-
证明在边长为1的正方形中任取10个点,则必存在两个点,该两点的距离不大于 2 3 \frac{\sqrt2}{3} 32。
-
用k种颜色给一个正五边形的顶点进行着色,共有多少不同的着色方案?再请给出只有黑、白(k=2)两种颜色时的每个具体染色方法。
更多真题
受限于篇幅,这里只给出了两年真题,更多真题、PDF版本、参考答案、资料等请前往开源仓库地址为https://gitee.com/Cheney822/nwpu-comb
欢迎大家在仓库里贡献自己的内容!!!
这篇关于组合数学历年真题-西北工业大学-持续更新中~的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






