本文主要是介绍MBA-历年数学条件充分判断,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
已知p,q 为非零实数. 则能确定 的值. (1)p+q=1 (2)
的值. (1)p+q=1 (2)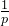 +
+  =1.
=1.
- p+q=1 ; p =1-q ;
=
=
=
;无法确定
+
=1;q =
;
=
*
=
*
= 1;可以确定
信封中装有10张奖券,只有1张有奖.从信封中同时抽取2张奖券,中奖的概率记为 P;从信封中每次抽取1张奖券后放回,如此重复抽取n次,中奖的概率记为Q.则P<Q;(1)n=2 ; (2)n=3
- P =
= 1/5 =0.2
- n=2次,Q = 1- 9/10 * 9/10 =0.19
- P > Q 不充分
- n=3次,Q = 1- 9/10 * 9/10 * 9/10 =0.271
- P < Q 充分
圆盘 x² + y² ≤ 2(x+y)被直线L分成简积相等的两部分;(1)L:x + y =2. (2)L:2x - y = 1
- x² + y² ≤ 2(x+y)
- x² - 2x +y²-2y ≤ 0
- 根据完全平方公式,补1 : (x² - 2x +1) + (y²-2y+1)=2
- (x-1)² + (y-1)² ≤ 2
- 所以圆心为(1,1),x=1,y =1
- 因此x + y =2和2x - y = 1 都符合要求。
已知a,b为实数,则a≥2 或 b≥2 ; (1)a+b≥4 (2)ab≥4
- 条件a + b ≥ 4, 必有a≥2 或 b≥2
- 条件 a b ≥4 , 因为ab可以同时等于负数,所以不能确定a≥2 或 b≥2
已知M=( )*(
)*( ),N=(
),N=( )*(
)*( ), 则M > N; (1)
), 则M > N; (1) 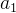 > 0 (2)
> 0 (2)  > 0
> 0
- 因为所有括号中都有
,
- M = (
+ t) * (t +
)
- N = (
+ t +
) * t
- 因为M > N,所有 (
+ t) * (t +
) > (
+ t +
) * t
- 换算
t +
+ t² +
t >
t + t² +
t
- 简化得
>0
已知{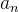 }是公差大于零的等差数列,
}是公差大于零的等差数列, 是{
是{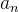 }的前n项和,则
}的前n项和,则 ≥
≥  ,n=1,2,...;
,n=1,2,...;
(1)  = 0 (2)
= 0 (2)  < 0
< 0
- 当
= 0,a0 ~ a9 都 小 0,a11及以上都大于0
- n=9时,
=
,其他
为最小值
- 因次
= 0成立
- 当
<0,所有当
<0,
>0
为最小值,
< 0 成立。
这篇关于MBA-历年数学条件充分判断的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






