模块二——滑动窗口：1658.将x减到0的最小操作数

本文主要是介绍模块二——滑动窗口：1658.将x减到0的最小操作数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、题目解析

题目链接：1658.将x减到0的最小操作数

这道题的意思是让我们求出x - (每次取数组最左边或者最右边的值) -> 0的最小操作次数并返回，否则返回-1。(PS:最左边和最右边的操作可以为0）

二、算法原理

题⽬要求的是数组「左端+右端」两段连续的、和为 x 的最短数组，信息量稍微多⼀些，不易理清思路；我们可以转化成求数组内⼀段连续的、和为sum(nums) - x 的最⻓数组。此时，就是熟悉的「滑动窗⼝」问题了。

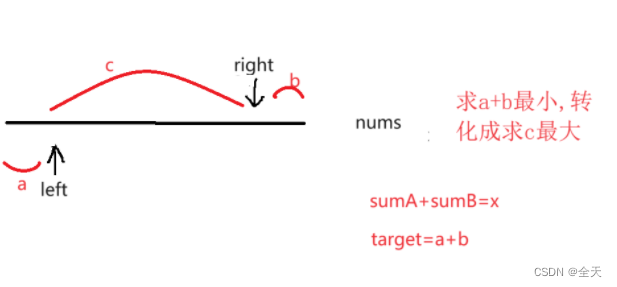
初始化左右指针left = 0 ,right = 0 （滑动窗⼝区间表⽰为[left,right) ，左右区间是否开闭很重要，必须设定与代码⼀致），当target<0时问题无解（数组总和小于x则再怎么减都无法减到0）。

三、代码编写

解法一：暴力枚举（超时）

class Solution {
public:int minOperations(vector<int>& nums, int x) {//暴力枚举int n = nums.size(),numsSum = 0,minOp = 0;for(int i = 0;i < n;i++){numsSum += nums[i];//求数组的总和}int target = numsSum - x;//target记录numsSum-xif(target < 0)return -1;else if(target == 0)return n;for(int left = 0;left < n;left++){int sum = 0;//记录left到right的总和for(int right = left;right < n;right++){sum += nums[right];if(target == sum)minOp = max(minOp,right - left + 1);}}if(minOp == 0)return -1;else return n - minOp;}
};

解法二：滑动窗口(时间复杂度是O(n),空间复杂度是O(1))

class Solution {
public:int minOperations(vector<int>& nums, int x) {//滑动窗口int n = nums.size(),minOp = -1,sum = 0;int numsSum = accumulate(nums.begin(), nums.end(), 0);//记录数组总和int target = numsSum - x;//转化问题if(target < 0)return -1;for(int left = 0,right = 0;right < n;right++){sum += nums[right];//进窗口while(sum > target)//判断sum -= nums[left++];if(target == sum)minOp = max(minOp,right - left + 1);//更新结果}if(minOp == -1)return -1;else return n - minOp;}
};

这篇关于模块二——滑动窗口：1658.将x减到0的最小操作数的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---