柏林噪声C++

本文主要是介绍柏林噪声C++，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

柏林噪声

随机噪声
在这里插入图片描述
如上图所示随机噪声没有任何规律可言，我们希望生成有一些意义的局部连续的随机图案

一维柏林噪声

在这里插入图片描述

假设希望生成一段局部连续的随机曲线，可以采用插值的方式：在固定点随机分配y值（一般是整数点），其他的点使用插值算法

方法一：线性插值的方式

公式如下：
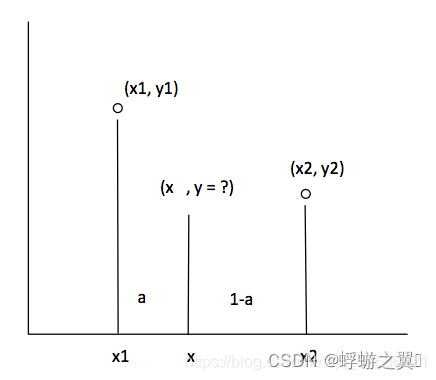
在这里插入图片描述
【数字图像处理】二维（2D）线性插值的应用
y = a*y1 + (1-a)*y2

我们画图看看：
在这里插入图片描述

import math
import numpy as np
import matplotlib.pyplot as pltperm = [151,160,137,91,90,15,131,13,201,95,96,53,194,233,7,225,140,36,103,30,69,142,8,99,37,240,21,10,23,190, 6,148,247,120,234,75,0,26,197,62,94,252,219,203,117,35,11,32,57,177,33,88,237,149,56,87,174,20,125,136,171,168, 68,175,74,165,71,134,139,48,27,166,77,146,158,231,83,111,229,122,60,211,133,230,220,105,92,41,55,46,245,40,244,102,143,54, 65,25,63,161, 1,216,80,73,209,76,132,187,208, 89,18,169,200,196,135,130,116,188,159,86,164,100,109,198,173,186, 3,64,52,217,226,250,124,123,5,202,38,147,118,126,255,82,85,212,207,206,59,227,47,16,58,17,182,189,28,42,223,183,170,213,119,248,152, 2,44,154,163, 70,221,153,101,155,167, 43,172,9,129,22,39,253, 19,98,108,110,79,113,224,232,178,185, 112,104,218,246,97,228,251,34,242,193,238,210,144,12,191,179,162,241, 81,51,145,235,249,14,239,107,49,192,214, 31,181,199,106,157,184, 84,204,176,115,121,50,45,127, 4,150,254,138,236,205,93,222,114,67,29,24,72,243,141,128,195,78,66,215,61,156,180]def perlin1D(x):# 整数x1和x2的坐标x1 = math.floor(x)x2 = x1 + 1# x1和x2的梯度值grad1 = perm[x1 % 255] * 2.0 - 255.0grad2 = perm[x2 % 255] * 2.0 - 255.0#x1和x2指向x的方向向量vec1 = x - x1vec2 = x - x2# x到x1的距离即vec1，利用公式3计算平滑参数t = 3 * pow(vec1, 2) - 2 * pow(vec1, 3)#梯度值与方向向量的乘积product1 = grad1 * vec1product2 = grad2 * vec2return product1 + t * (product2 - product1)def linear1D(x):# 整数x1和x2的坐标x1 = math.floor(x)x2 = x1 + 1# y值 随机数grad1 = perm[x1 % 255] * 2.0 - 255.0grad2 = perm[x2 % 255] * 2.0 - 255.0t=x - x1return grad1 + t * (grad2 - grad1)def linear1D_plus(x):# 整数x1和x2的坐标x1 = math.floor(x)x2 = x1 + 1# x1和x2的梯度值grad1 = perm[x1 % 255] * 2.0 - 255.0grad2 = perm[x2 % 255] * 2.0 - 255.0#x1和x2指向x的方向向量vec1 = x - x1vec2 = x - x2t=x - x1#梯度值与方向向量的乘积product1 = grad1 * vec1product2 = grad2 * vec2return product1 + t * (product2 - product1)def draw1D():# 绘制散点图x0=[]y0=[]for i in range(11):x0.append(i)y0.append( perm[i] * 2.0 - 255.0)plt.scatter(x0, y0,color='red')# 绘制1D的图像x = np.linspace(0, 10, 100)y = np.zeros(100)y1 = np.zeros(100)y2 = np.zeros(100)for i in range(100):y[i] = perlin1D(x[i])y1[i] = linear1D(x[i])y2[i] =linear1D_plus(x[i])# 绘制图像plt.plot(x, y,color='deepskyblue')plt.plot(x, y1,color='green')plt.plot(x, y2,color='orange')plt.show()draw1D()

线性插值

x取[0,10]这个区间，y在整数点随机取值，非整数点使用线性插值
ps 随机值使用伪随机数perm，柏林噪声在图像领域使用，颜色的取值范围是[0,255]，所以perm的值也是[0,255]
上图红色的点是：整数点随机取值的结果，绿色的线是线性插值。
$y = t * y 2 + (1 - t) * y 1 = y 1 + t (y 2 - y 1)$
$t = x - x 1$

线性插值plus

我们希望它更平滑一点，如果插值点x的值y与附近点x1,x2的位置相关
所以改进上述算法：
$y = t * y 2 * w 2 + (1 - t) * y 1 * w 1 = y 1 * w 1 + t (y 2 * w 2 - y 1 * w 1)$
w是权重系数，也是柏林算法中的方向向量vec1 = x - x1
如图中黄色的线

柏林噪声

柏林噪声在此基础上再加强一步：
$t=3t^2 -2t^3$

算法步骤：
input: x

计算周围的点：x1 , x2
计算x1 , x2 梯度 : grad1， grad2 随机取[0,255]
方向向量: (vec1 =x-x1 ;vec2 = x-x2)
梯度值与方向向量的乘积 product=grad*vec
计算系数 t=3t^2 -2t^3
插值：y = product1 + t * (product2 - product1)
output :y

根据上述原理可以画一个不规则的圆形

def drawCircle():#画圆形# 创建一个坐标系fig, ax = plt.subplots()# 定义圆心和半径center = (0, 0)radius = 10# 生成圆的数据theta = np.linspace(0, 2*np.pi, 100)x = radius * np.cos(theta) + center[0]y = radius * np.sin(theta) + center[1]y1 = np.zeros(100)for i in range(100):y1[i] = y[i]+ perlin1D(theta[i]*5)/255*2# 画出圆形ax.plot(x, y,color='orange')ax.plot(x, y1,color='deepskyblue')# 设置坐标轴范围ax.set_xlim([-15, 15])ax.set_ylim([-15, 15])# 显示图像plt.show()