CSP认证 201312-4有趣的数[C++题解]：组合数、数学

本文主要是介绍CSP认证 201312-4有趣的数[C++题解]：组合数、数学，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

- - 题目解答
  - 题目链接

题目解答

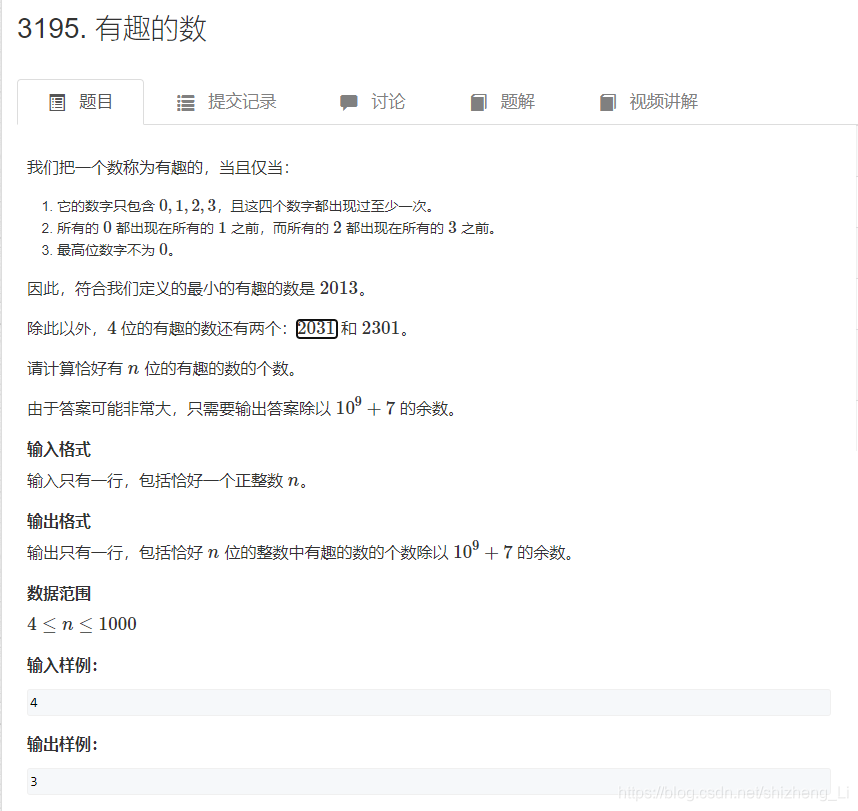
在这里插入图片描述
来源：acwing

分析：
题目要求：n位数，只能放0，1，2，3；0必须在1前面，2必须在3前面；0不能放在首位。

由于0和1有限制关系，2和3有限制关系，所以把它们分成两组。总共有n位，用组合数学的角度来考虑。具体思考过程如下图所示，n位中0和1这一组占多少位，剩下的位数让2和3来占。

不失一般性，对于A组占k位，B组占n-k位这种情况进行分析：

A组（0和1）占k位，由于0永远排在1前面，且0不能排在首位，所以A组可取的情况是 $C_{n-1}^{k}$ ,含义是：在除第一位的情况下，剩下的n-1位中选k位填0或者1，这样的话，其余的位置就填2或者3.

所以，接着考虑组内问题。对于0和1占k位，假设其中有t个0，则有k-t个1，而且呢，0只能排在1前面，所有组内的情况是和t有关，t至少为1，最大为k-1，所以共有k-1种情况。同理，对于2和3占n-k位，共有n-k-1种情况。

所以，对于对于A组占k位，B组占n-k位这种情况，总共有 $C_{n-1}^{k} \times (k-1) \times(n-k-1)$

则总的情况是 $\Sigma_{k=2}^{n-2}C_{n-1}^{k} \times (k-1) \times(n-k-1)$

在这里插入图片描述
如何求组合数呢？参见笔者的另一篇博文：算法刷题-数论-组合数、快速幂、逆元、递推求组合数、逆元求组合数

ac代码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1010;
const int mod = 1e9 + 7;
int c[N][N];//组合数数组
int n;int main(){cin >> n;//预处理，求组合数 c[i][j]表示i个数中选j个for(int i = 0; i<= n; i++ )for( int j = 0; j<= i; j++)if(!j) c[i][j] =1;else c[i][j] = (c[i-1][j] + c[i-1][j-1]) % mod;LL res = 0;for(int k = 2; k <= n-2; k++)res =  (res + (LL)c[n-1][k] * (k-1) * (n-k-1) % mod) % mod;cout << res <<endl;
}