【NOIP2017提高组正式赛】Day1T3逛公园

Description

   策策同学特别喜欢逛公园。公园可以看成一张o个点n条边构成的有向图，且没有自环和重边。其中1号点是公园的入口，o号点是公园的出口，每条边有一个非负权值，代表策策经过这条边所要花的时间。策策每天都会去逛公园，他总是从1号点进去，从o号点出来。策策喜欢新鲜的事物，他不希望有两天逛公园的路线完全一样，同时策策还是一个特别热爱学习的好孩子，他不希望每天在逛公园这件事上花费太多的时间。如果1号点到o号点的最短路长为e，那么策策只会喜欢长度不超过e + k的路线。策策同学想知道总共有多少条满足条件的路线，你能帮帮他吗？为避免输出过大，答案对p取模。如果有无穷多条合法的路线，请输出−1。

Input

输入文件名为 park.in 。
第一行包含一个整数 T, 代表数据组数。
接下来T组数据，对于每组数据：
第一行包含四个整数 O,N,K,P，每两个整数之间用一个空格隔开。
接下来N行，每行三个整数， 代表编号为的点之间有一条权值为 的有向边，每两个整数之间用一个空格隔开。
Output
输出文件包含 T行，每行一个整数代表答案。

Sample Input

2
5 7 2 10
1 2 1
2 4 0
4 5 2
2 3 2
3 4 1
3 5 2
1 5 3
2 2 0 10
1 2 0
2 1 0

Sample Output

3
-1

样例说明：
对于第一组数据，最短路为 3。
1 – 5, 1 – 2 – 4 – 5, 1 – 2 – 3 – 5 为 3 条合法路径。

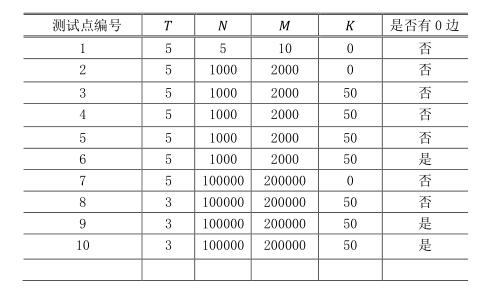
数据范围

题解

求最短路是很简单的，
如果只求最短路的路径数也是很简单的，
设$f_i$表示从点1到点i的最短路路径条数，
转移的时候就判断当前边是不是在最短路上面，是就转移。

现在要求比最短路大k的，
很自然地想到设多一维，
用$f_{j,i}$表示比当前最短路大j，到达点i的路径数。

关于转移，就有所不同了，
要用拓扑序，而且要先枚举比最短路大多少，

对于有无穷解的情况，就是存在一个权值为0的环在最短路上面。

code

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <iostream>
#define ll long long
#define N 100003
#define inf 1125899906842624
using namespace std;char ch;
void read(int& n)
{n=0;for(ch=getchar();ch<'0' || ch>'9';ch=getchar());for(;'0'<=ch && ch<='9';n=(n<<3)+(n<<1)+ch-48,ch=getchar());
}int nxt[N*2],to[N*2],last[N*2],tot;
int nxt1[N*2],to1[N*2],last1[N*2],tot1;
int nxt2[N*2],to2[N*2],last2[N*2],tot2,g[N];
ll v[N*2],v1[N*2],dis[N],dis1[N];
int T,n,m,k,p,x,y,z;
int d[N*200],head,tail;
ll f[53][N],ans;
bool bz[N],check;void ins(int x,int y,int z)
{nxt[++tot]=last[x];to[tot]=y;v[tot]=z;last[x]=tot;
}void ins1(int x,int y,int z)
{nxt1[++tot1]=last1[x];to1[tot1]=y;v1[tot1]=z;last1[x]=tot1;
}void ins2(int x,int y)
{nxt2[++tot2]=last2[x];to2[tot2]=y;last2[x]=tot2;g[y]++;
}void spfa()
{memset(bz,1,sizeof(bz));memset(dis,127,sizeof(dis));dis[tail=1]=bz[d[1]=1]=head=0;while(head<tail){x=d[++head];for(int i=last[x];i;i=nxt[i])if(dis[x]+v[i]<dis[to[i]]){dis[to[i]]=dis[x]+v[i];if(bz[to[i]]){bz[to[i]]=0;d[++tail]=to[i];}}bz[x]=1;}
}void spfa1()
{memset(bz,1,sizeof(bz));memset(dis1,127,sizeof(dis1));dis1[d[tail=1]=n]=bz[n]=head=0;while(head<tail){x=d[++head];for(int i=last1[x];i;i=nxt1[i])if(dis1[x]+v1[i]<dis1[to1[i]]){dis1[to1[i]]=dis1[x]+v1[i];if(bz[to1[i]]){bz[to1[i]]=0;d[++tail]=to1[i];}}bz[x]=1;}
}void pre()
{head=tail=0;for(int i=1;i<=n;i++)if(g[i]==0)d[++tail]=i;while(head<tail){x=d[++head];for(int i=last2[x];i;i=nxt2[i])if(--g[to2[i]]==0)d[++tail]=to2[i];}
}void add(ll& x,ll y)
{x=y+x>p?y+x-p:y+x;
}int main()
{freopen("park.in","r",stdin);freopen("park.out","w",stdout);read(T);while(T--){read(n);read(m);read(k);read(p);memset(last,0,sizeof(last)); memset(last1,0,sizeof(last1));  memset(last2,0,sizeof(last2)); memset(g,0,sizeof(g));ans=tot=tot1=tot2=0;for(int i=1;i<=m;i++)read(x),read(y),read(z),ins(x,y,z),ins1(y,x,z);spfa();spfa1();for(int i=1;i<=n;i++)for(int j=last[i];j;j=nxt[j])if(dis[i]+v[j]==dis[to[j]])ins2(i,to[j]);pre();check=0;for(int i=1;i<=n;i++)if(g[i] && dis[i]+dis1[i]<=dis[n]+k){check=1;break;}if(check){printf("-1\n");continue;}memset(f,0,sizeof(f));f[0][1]=1;for(int i=0;i<=k;i++)for(int j=1;j<=tail;j++){x=d[j];if(dis[x]>inf || dis1[x]>inf)continue;if(dis[x]+dis1[x]+i>dis[n]+k)continue;for(int p=last[x];p;p=nxt[p]){ll t=dis[x]+v[p]+i-dis[to[p]];if(t<=k)add(f[t][to[p]],f[i][x]);}}ans=0;for(int i=0;i<=k;i++)add(ans,f[i][n]);printf("%lld\n",ans);}return 0;
}