左式堆(leftist heap)

本文主要是介绍左式堆(leftist heap)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

堆合并

堆合并是指，对于任意两个堆，将其合并为一个更大的堆，如下图所示：

heap_merge

为了解决这个问题，我们可以首先进行一些初步的尝试。

简明的插入策略

最简明的思路，无非是将一个堆中的元素，逐个删除并且依次插入到另一个堆中。不妨设两个堆的规模分别为m和n，则这种策略的时间复杂度为O(m * (logm + log(m + n))) = O(m * log(m + n))。

Floyd批量建堆算法

简明的插入策略的时间复杂度是在是太差，实际上，我们可以将这m + n个元素组织成一个向量，使用Floyd建堆算法，其时间复杂度为O(m +n )。

实际上，Floyd建堆算法对于任意一组输入数据都可以达到线性的时间复杂度，但是这里的输入并非是【任意】的输入，而是两个堆，它们在内部都是满足堆序性质的。因此我们期望这种预先满足的堆序性质得到利用，从而在一定程度上得到一个更高效率的堆合并算法。

一种递归策略

下面给出一种递归地进行堆合并的策略——设两个堆分别为A和B，并且保证A堆的堆顶大于B堆的堆顶，为了将A，B两个堆合并，只需要取出A的右子树，将A的右子树与B进行合并，并且将合并后的堆重新作为A的右子树。而为了将A的右子树与B合并，只需要递归地进行上述的策略即可。

这种策略的正确性是显然的，一次这样的操作后，合并后的堆，其堆序性质仍然得到满足。通过不断地取堆的右子树，递归问题的规模不断减小，直到平凡的情况，即A的右子树为空，此时直接将B堆连接到A的右子树即可，因此该算法是有穷的。

对该算法进行进一步分析，在最坏的情况下，需要不断穷举A和B的右子树，直到两个堆的规模都只有1，因此在最坏情况下，该算法需要进行rh1 + rh2次递归，其中rh1和rh2分别表示两个堆的最右侧路径长度。

为了快速地取出堆的右子树，以及将某棵树连接到一个节点上，这里应该抛弃前面在完全二叉堆采用的向量结构，而是采用二叉树来作为堆的底层结构，此时每次递归的时间复杂度都是O(1)，因此整体的时间复杂度为O(rh1 + rh2)。可见，为了获得更好的性能，就应该尽量减少堆的最右侧路径长度，左式堆就是这样的一种结构。

左式堆的概念

首先需要引入空节点路径长度的概念——对任意一棵二叉树，引入所有的外部节点，则任意节点的空节点路径长度(npl, null path length)，定义为该节点到外部节点的最短距离，外部节点的npl定义为零，即npl(null) = 0。

因此，任意内部节点x的空节点路径长度，取决于其左右节点中npl的更小者，即

npl(x) = MIN(npl(lc(x)), npl(rc(x))) + 1;

对于左式堆中的任一节点，都满足其左孩子的npl值，不小于右孩子的npl值，即左倾性：

npl(lc(x)) >= npl(rc(x));

根据npl的定义，左式堆中的任一节点的npl都唯一地取决于它的右孩子，即

npl(x) = npl(rc(x)) + 1;

这样，对于左式堆的根节点，其npl等于其右子树的npl加一，而它的右子树的npl，又等于它的右子树的右子树的npl加一，即

npl(root) = npl(rc(root)) + 1 = npl(rc(rc(root))) + 2 = ... = right path length

因此，根节点的外部路径长度npl，就等于最右侧路径长度。左式堆的一个实例如下图所示：

leftist_heap

而让我们再回顾一下npl的定义，即任一节点到外部节点路径的最短距离，因此根节点到外部节点的最短路径，就是左式堆的最右侧路径。设最右侧路径的长度为d，左式堆中一定包含了以d为高度的一棵满子树，因此左式堆的全部节点数量（包括外部节点）n一定满足

$\ge 2^{d + 1} - 1$

反过来，即d一定满足

$\le log_2^{n + 1} = O(logn)$

左式堆的该性质如下图所示：

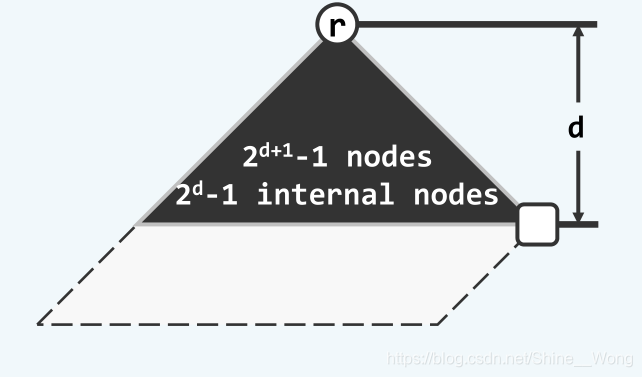
在这里插入图片描述

在这样的条件下，我们上面给出的合并算法，其时间复杂度就只有O(logm + logn)了，这无疑是对性能的一次极大改进。但是需要注意的是，左式堆只是保证最右侧路径的长度最小，并非左子堆的规模和高度一定会大于右子堆。

左式堆的实现

左式堆仍然是优先级队列的一种实现方式，因此要实现左式堆，仍然只需要实现优先级队列的几个抽象函数接口，即getMax，insert和delMax。其中getMax的实现只需取出左式堆的根节点即可，与完全二叉堆的实现相同，在这里不再赘述。

需要指出的是，左式堆的insert接口与delMax接口，都可以借助左式堆的merge算法快速的实现。对于insert接口，无非将一个规模为1的左式堆，与当前的左式堆进行合并，其代码如下：

template <typename K, typename V>
void LeftHeap<K, V>::insert(entry<K, V> e){BinNodePosi(T) newNode = new BinNode<T>(e);newNode->npl = 1;__root = merge(__root, newNode);__root->parent = nullptr;++__size;
}

而左式堆的delMax函数，无非是在删除了根节点以后，将根节点的两个左子堆进行合并，利用merge也可以方便地实现：

template <typename K, typename V>
entry<K, V> LeftHeap<K, V>::delMax(){entry<K, V> res = getMax();__root = merge(__root->leftChild, __root->rightChild);if (__root) __root->parent = nullptr;--__size;return res;
}

因此，问题的关键就在于左式堆的merge函数，该函数基本按照我们上面提到过的策略进行，只是需要做一些细节上的修改。无论是在insert还是delMax操作的过程中，都需要动态地维护左式堆的结构，即每次将合并后的堆作为右子树插入到当前节点后，都需要对当前节点的左倾性进行检查，一旦发现左子树的npl小于右子树，则将左右子树交换。merge函数的实现如下：

#define T entry<K, V>template<typename K, typename V>
BinNodePosi(T) merge(BinNodePosi(T) a, BinNodePosi(T) b){if (a == nullptr) return b;if (b == nullptr) return a;BinNodePosi(T) temp;if (a->data < b->data){//swap a and btemp = a;a = b;b = temp;}if (a->rightChild == nullptr) a->rightChild = b;else a->rightChild = merge(a->rightChild, b);a->rightChild->parent = a;if (NPL(a->leftChild) < NPL(a->rightChild)) {// swap the right chlid and left child of atemp = a->leftChild;a->leftChild = a->rightChild;a->rightChild = temp;}a->npl = NPL(a->rightChild) + 1;return a;
}