LeetCode —— 1312. 让字符串成为回文串的最少插入次数

本文主要是介绍LeetCode —— 1312. 让字符串成为回文串的最少插入次数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目描述

给你一个字符串 s ，每一次操作你都可以在字符串的任意位置插入任意字符。

请你返回让 s 成为回文串的 最少操作次数 。

「回文串」是正读和反读都相同的字符串。

示例

示例一

输入：s = "zzazz"
输出：0
解释：字符串 "zzazz" 已经是回文串了，所以不需要做任何插入操作。

示例二

输入：s = "mbadm"
输出：2
解释：字符串可变为 "mbdadbm" 或者 "mdbabdm" 。

示例三

输入：s = "leetcode"
输出：5
解释：插入 5 个字符后字符串变为 "leetcodocteel" 。

示例四

输入：s = "g"
输出：0

示例五

输入：s = "no"
输出：1

解题思路

这道题的解法是动态规划，我们就拿下面这个字符串举例：

首先对于每个单个的字符来说，其肯定是回文串。那么假如我们构建的dp[i][j]来表示i~j范围内构成回文串所需要的步骤数。那么这个矩阵的对角线元素则均为0。

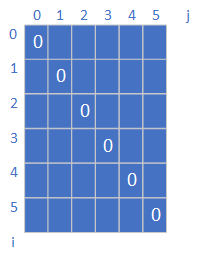
那么根据我们对dp的理解，我们知道i不会超过j的，所以对于左下角矩阵实际上是不用填充的，我们要填充的只有右上角的矩阵。

对于dp[i][j]来说，我们现在能够拿到dp[i+1][j-1]的值（其中dp[i+1][j-1]表示i+1到j-1范围内元素是否是回文的），那么dp[i][j]就有以下几种情况：

• 第一种就是s[i] == s[j]，在这种情况下，dp[i][j] = dp[i+1][j-1]：
  
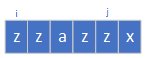
• 第二种就是s[i] ！= s[j]：
  

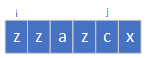
这种情况下，我们我们可以在i的右边加上c使得s[i+1]~s[j]成为一个回文串。或者在j的左边加上z，使得s[i]~s[j-1]成为一个回文串，之后取这两个步骤最少的那一步。那么假设现在我们在i的右边加上c了，那么此时我们只需要在这个回文串的右边（也就是j的右边）加上z就可以构成回文了。

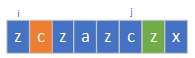
代码呈现

class Solution {
public:/*** @brief leetcode提供的函数* * @param s 待构成回文的字符串* @return int 构成回文的最少步骤*/int minInsertions(string s) {int s_size = s.size();vector<vector<int>> dp(s_size,vector<int>(s_size,0));for(int i =s_size-2;i>=0;i--){for(int j = i+1;j<s_size;j++){if(s[i] == s[j]){dp[i][j] = dp[i+1][j-1];}else{dp[i][j] = min(dp[i+1][j],dp[i][j-1])+1;}}}return dp[0][s_size-1];}
};

参考文献

[1] labuladong的算法小抄[M].付东来

这篇关于LeetCode —— 1312. 让字符串成为回文串的最少插入次数的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---