本文主要是介绍XTU OJ 1339 Interprime 学习笔记,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
链接
传送门
代码
#include<bits/stdc++.h>
using namespace std;const int N=1e6+10;
//78498 我计算了一下,6个0的范围内有这么多个素数,所以开这么大的数组存素数
//计算的代码是一个循环
int prime[80000];
int a[N],s[N];//s数组是前缀和数组bool isprime(int a)//判断素数的模板函数
{if(a<2) return false;for(int i=2;i*i<=a;i++){if(a%i==0) return false;}return true;
}int main()
{int cnt=0;for(int i=0;i<N;i++){if(isprime(i)){prime[++cnt]=i;//这表示从下标为1的位置开始计算}//找出所有的素数}// for(int i=1;i<1000;i++)
// {
// printf("%d\n",prime[i]);
// }for(int i=1;i<cnt;i++){int temp=prime[i]+prime[i+1];temp/=2;if((prime[i]%2!=0)&&(prime[i+1]%2!=0)&&(!isprime(temp))){a[temp]=1;}}//printf("%d\n",a[15]);for(int i=3;i<N;i++){if(a[i]==1){s[i]=s[i-1]+1;//前缀和的使用,前缀和就是说//前面的数据已经被处理过了,比如说处理到i这个位置,i-1这个位置//已经被处理过了,可以直接使用,就不需要从头开始多次计算//本来要计算1到i-1,1到i,现在不需要计算1到i,所以降低了时间复杂度}else{s[i]=s[i-1];}}int t;scanf("%d",&t);while(t--){int c,d;scanf("%d%d",&c,&d);printf("%d\n",s[d]-s[c-1]);//这里可以理解成//图片这种,是前缀和的公式,可以直接记住}return 0;
}计算素数个数的代码
#include<bits/stdc++.h>
using namespace std;bool isprime(int a)
{if(a<2) return false;for(int i=2;i*i<=a;i++){if(a%i==0) return false;}return true;
}int main()
{int cnt=0;for(int i=0;i<=1e6;i++){if(isprime(i)){cnt++;}}printf("%d\n",cnt);return 0;
}用于理解前缀和的图片
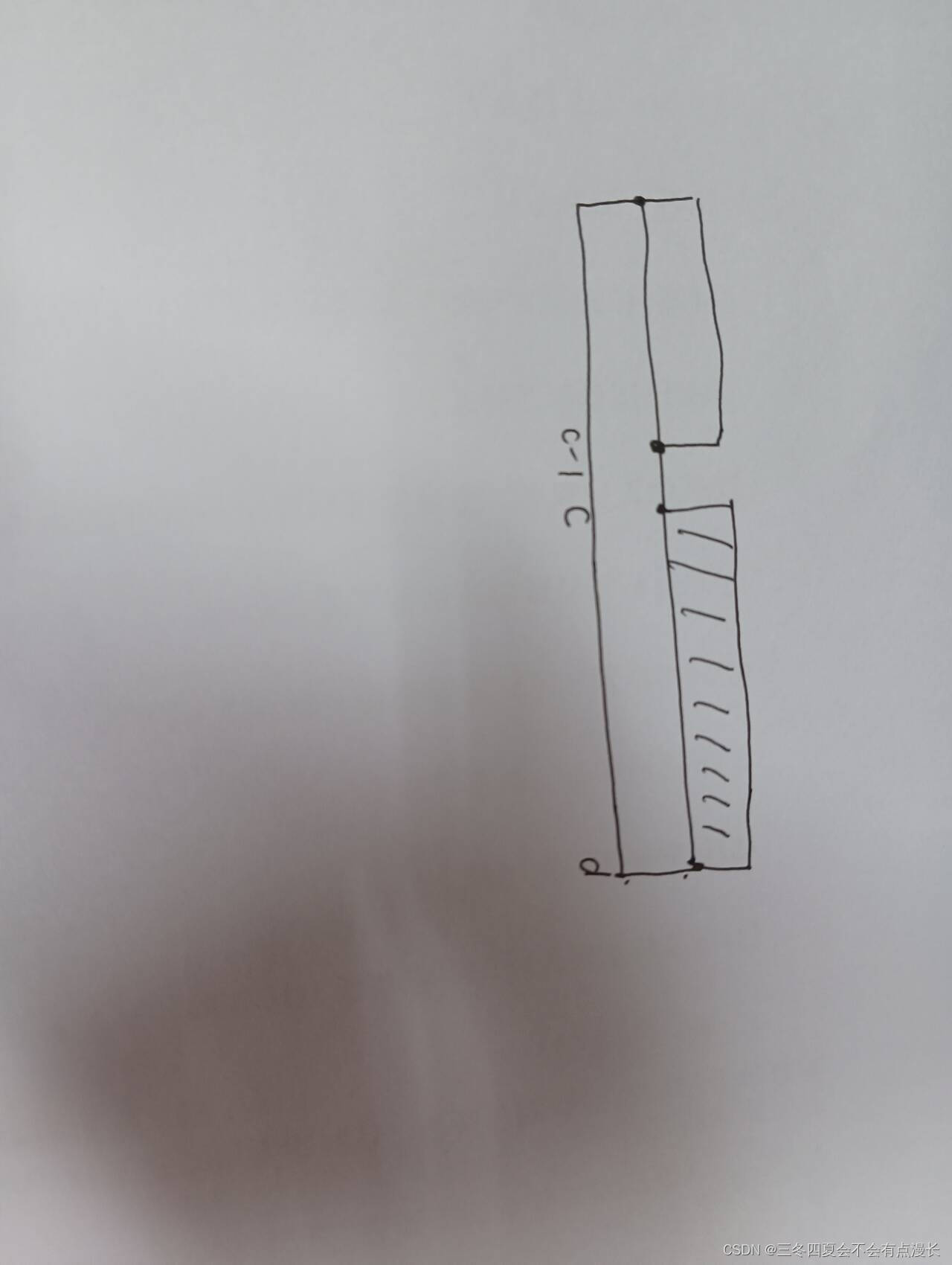
总结
1.该题考查前缀和,通过前缀和来降低时间复杂度,原理写在代码注释中了,连续的素数应该要怎么处理?把素数提取出来存在数组中,怎么提取出来?用一个计数器作为数组下标,++cnt表示的是使用自增之后的数字,也就是说,cnt初始化为0的话,是从1开始保存素数的
2.a数组用来保存所谓的内部素数的状态,把内部素数作为a数组的下标,把数组的数值标记为1,建立一个下标和数值之间的映射关系
3.最后是遍历整个区间,寻找有多少个被标记的a数组,使用前缀和,从而得出答案
4.前缀和的公式就是最后输出的那个s[d]-s[c-1]
5.前面都属于打表(循环遍历预处理所有元素,把有需要的元素存在数组里面)
这篇关于XTU OJ 1339 Interprime 学习笔记的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








