本文主要是介绍Codeforces Round 907 (Div. 2) (C 贪心 D套路? F dfs序+差分树状数组),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
A:
这种操作题,每次先想这个操作有什么性质
对于2^0来说可以操作 第1位
对于2^1来说可以操作 第1-2位
对于2^2来说可以操作 第1-4位 (第3位无法单独修改)
对于2^3来说可以操作 第1-8位(第5 6 7位无法单独修改)
可以观察到我们要求无法修改的数要按顺序才能满足
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+10,mod= 998244353;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;
const long long inf=1e17;
int n,m,k;
vector<int> g[N];
int a[N];
void solve()
{cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=2;i<=5;i++){bool ok=true;// cout<<pow(2,i-1)<<" "<<pow(2,i)<<"\n";for(int j=pow(2,i-1)+1;j<pow(2,i);j++){if(j+1>n||j>n) break;if(a[j]<=a[j+1]) continue;ok=false;} if(!ok){cout<<"NO\n";return ;}}cout<<"YES\n";
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}B:
操作题,还是想操作当前数x对每个数组a的每个数有啥影响
如果当前数a[i]可以整除2^x,然后加上2^(x-1),那么下次这个数就不能整除2^x
那么他就会变成2^(x-1)的倍数了,他的因子不包含2^x,所以不会再操作
然后x最多30个数,去重后操作即可
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+10,mod=1e9+7;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;
const long long inf=1e17;
int n,m,k;
vector<int> g[N];
int a[N];class BitTree {public:vector<int> tree;int n;BitTree(int _n) : n(_n) {tree.resize(n+1);fill(tree.begin(),tree.end(),0);}inline int lowbit(int x) { return x&-x; }inline void Modify(int x,int v) {for(;x<=n;x+=lowbit(x)) tree[x]+=v;}inline int q(int x) {int ret=0;if(x<=0) return 0;for(;x;x-=lowbit(x)) ret+=tree[x];return ret;}inline int Query(int l,int r) {return q(r)-q(l-1);}
};
int l[N],r[N];
void solve()
{vector<int> b;map<int,int> mp;cin>>n>>m;for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=m;i++){int x;cin>>x;if(mp.count(x)) continue;mp[x]++;b.push_back(x);}for(int i=1;i<=n;i++){int x=a[i];for(auto y:b){if(x%(1<<y)==0){x+=(1<<y-1);}}cout<<x<<" \n"[i==n];}}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}C:贪心,肯定是积个大的秒后面数量多的,然后当操作最后一个数的时候,尽量别浪费当前计数器的数,要分奇偶性和1,比如8,前面已经有2了,那么再操作2次,计数器变成4,操作个计数器秒掉,如果当前是8,前面计数器是3,为了不浪费计数器,最后一次肯定是直接消灭而不是使用计数器,所以先-1变成偶数(如果不这样做,最后计数器会多1,次数可能会增加),再换成偶数操作即可,特判1
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+10,mod= 998244353;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;
const long long inf=1e17;
int n,m,k;
vector<int> g[N];
int a[N];
void solve()
{cin>>n;for(int i=1;i<=n;i++) cin>>a[i];sort(a+1,a+1+n);int res=0;int l=1,r=n;int sum=0;while(l<=r){if(a[l]==0){l++;continue;}if(l==r){if(a[l]==1){res++;break;}if((a[l]-sum)%2==1){res+=(a[l]-sum)/2+1;res++;}else{res+=(a[l]-sum)/2+1;}cout<<res<<"\n";return ;}if(a[r]<=sum+a[l]){int x=a[r]-sum;res+=x+1;a[l]-=x;r--;sum=0;} else{sum+=a[l];res+=a[l];l++; }}cout<<res<<"\n";
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}D:套路题,求两个区间差即可
然后我画图你应该能看懂

g的函数的值最多有两个不同,因为3 4 5...的增长比2增长快,所以最多两个
可以观察到g的值怎么求
比如8 到 15
用3的倍数求
16到31用 4倍数求他们的g的值,然后乘上求区间个数即可
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+10,mod=1e9+7;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;
const long long inf=1e17;
int n,m,k;
vector<int> g[N];
int a[N];
void solve()
{auto get=[&](int x){int res=0;int c=2;for(int i=4;i<=x;i*=2){int cnt=0;int r=min(x,i*2-1);__int128 now=1;while(now<=i) cnt++,now*=c;c++;if(now>r){res+=(r-i+1)%mod*(cnt-1)%mod;}else{int t=r-now+1;t%=mod;res+=t*cnt%mod+(now-i)%mod*(cnt-1);}}return res%mod;};int l,r;cin>>l>>r;cout<<((get(r)-get(l-1))%mod+mod)%mod<<"\n";
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}F:首先肯定要把数dfs一遍弄出来把,不然鬼知道子树有哪些
然后我们把树画出来
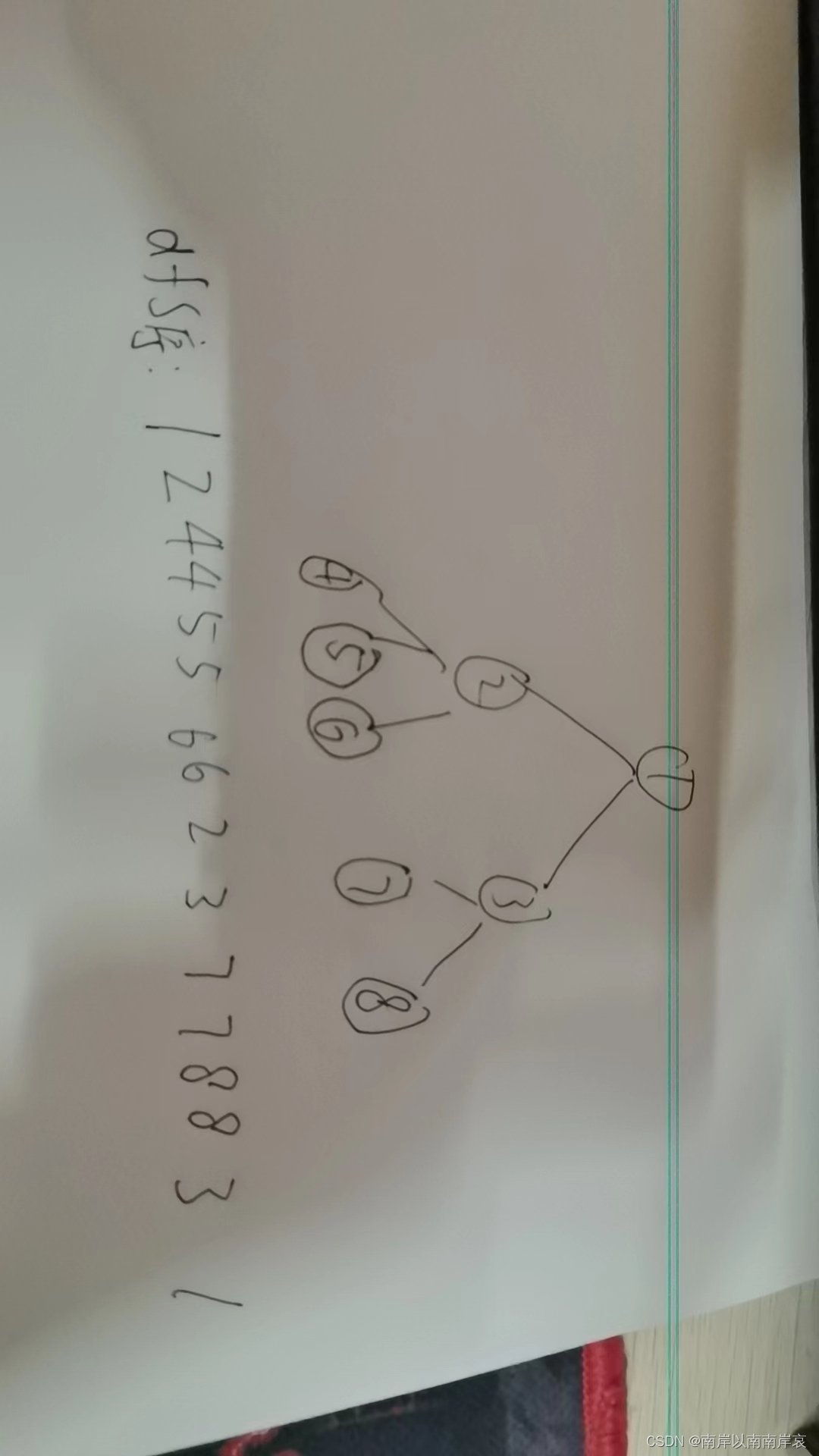
假设 5是新增的节点,我们怎么操作,
直接把前面5节点的数全部减成0即可
然后就是差分咯,因为子树增加是增加整个区间的
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+10,mod=1e9+7;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;
const long long inf=1e17;
int n,m,k;
vector<int> g[N];
int a[N];class BitTree {public:vector<int> tree;int n;BitTree(int _n) : n(_n) {tree.resize(n+1);fill(tree.begin(),tree.end(),0);}inline int lowbit(int x) { return x&-x; }inline void Modify(int x,int v) {for(;x<=n;x+=lowbit(x)) tree[x]+=v;}inline int q(int x) {int ret=0;if(x<=0) return 0;for(;x;x-=lowbit(x)) ret+=tree[x];return ret;}inline int Query(int l,int r) {return q(r)-q(l-1);}
};
int l[N],r[N];
void solve()
{cin>>n;for(int i=1;i<=n*2+10;i++)g[i].clear();vector<array<int,3>>query;int now=1;for(int i=0;i<n;i++){int op;cin>>op;if(op==1){now++;int v;cin>>v;query.push_back({op,v,0});g[v].push_back(now);}else{int v,x;cin>>v>>x;query.push_back({op,v,x});}}int dfn=0;function<void(int)> dfs=[&](int u){l[u]=++dfn;for(auto v:g[u]){dfs(v);}r[u]=++dfn;};dfs(1);BitTree tr(n*2+10);now=1;for(auto [op,v,x]:query){if(op==1){//v增加一个子节点now++;int t=tr.q(l[now]);tr.Modify(l[now],-t);tr.Modify(r[now],t);}else{tr.Modify(l[v],x);tr.Modify(r[v],-x);}}for(int i=1;i<=now;i++){cout<<tr.q(l[i])<<" \n"[i==now];}
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();
}这篇关于Codeforces Round 907 (Div. 2) (C 贪心 D套路? F dfs序+差分树状数组)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





