2021-10-14 剑指offer2：37~48题目+思路+多种题解

写在前面

本文是采用python为编程语言，作者自行练习使用，题目列表为：剑指 Offer（第 2 版），未使用实体书，难度未标注的均为“简单”，我也不是很清楚为什么有几个编号没有提供。“《剑指 Offer（第 2 版）》通行全球的程序员经典面试秘籍。剖析典型的编程面试题，系统整理基础知识、代码质量、解题思路、优化效率和综合能力这 5 个面试要点。”，本文中的思路来源于每道题目中的题解部分，争取提供全面，优化后的题解，其中所有代码已通过题目检验。

剑指 Offer 37. 序列化二叉树（困难）

题目

思路

• 序列化：层次遍历，然后再恢复回去即可。层次遍历就是bfs，注意遇见null的情况不是不再添加，而是append(“null”)即可。且“序列化”的含义是“变成字符串形式”，所以不要使直接用node.val，最后的返回也一定是个字符串！
• 反序列化：按照层次，空的结点跳过，非空的结点一个左一个右即可。这里仍然需要借助队列，已经添加到左右子树的结点也需要加入到队列之中，以方便后面下层的添加。

题解

• BFS层次遍历：

class Codec:def serialize(self, root):if not root: return "[]"queue = []queue.append(root)res = []while queue:node = queue.pop(0)if node:res.append(str(node.val))queue.append(node.left)queue.append(node.right)else: res.append("null")return '[' + ','.join(res) + ']'def deserialize(self, data):if data == "[]": returnnodes = data[1:-1].split(',')root = TreeNode(int(nodes[0]))queue = []queue.append(root)i = 1while queue:node = queue.pop(0)if nodes[i] != "null":node.left = TreeNode(int(nodes[i]))queue.append(node.left)i += 1if nodes[i] != "null":node.right = TreeNode(int(nodes[i]))queue.append(node.right)i += 1return root

• DFS遍历（因为未规定序列化的标准，所以可以以任何一种方式序列化，这里放DFS的意义是为了展示如何递归的完成反序列化）：

class Codec:def serialize(self, root):if not root:return 'None'return str(root.val) + ',' + str(self.serialize(root.left)) + ',' + str(self.serialize(root.right))def deserialize(self, data):def dfs(nodes):val = nodes.pop(0)if val == 'None':return Noneroot = TreeNode(int(val))root.left = dfs(nodes)root.right = dfs(nodes)return rootnodes= data.split(',')return dfs(nodes)

剑指 Offer 38. 字符串的排列（中等）

题目

思路

• dfs深度遍历：注意遍历开始不再是第一位，而是一个空字符串，目的是让第一位也参与遍历。dfs的精髓在于回溯，而不是拘泥于一个左子树一个右子树。

题解

• 递归：

class Solution:def permutation(self, s: str) -> List[str]:res = []vis = [0]*len(s)def dfs(track):if len(track) == len(s) and track not in res:res.append(track)return for j in range(len(s)):if vis[j]:continuevis[j] = 1dfs(track+s[j])# 随着每一场的深度遍历完成，进行标志位归0，以方便下一次深度遍历vis[j] = 0dfs('')return res

• 递归的改进：1. 重复元素不用重复排列，进行剪枝(这一步上面的方法是使用的track not in res，但可以在构成时就不去遍历) 2. 不要重复对不可变的字符串进行操作，而是使用列表，最后再join 3.以列表作为参数会比较慢，所以考虑一种新的思路：以传统的dfs位数作为参数，对每一位进行for循环的交换。

class Solution:def permutation(self, s: str) -> List[str]:tmp, res = list(s), []def dfs(n):if n == len(tmp) - 1:res.append(''.join(tmp))returncutset = set()for i in range(n, len(tmp)):if tmp[i] in cutset: continue cutset.add(tmp[i])tmp[i], tmp[n] = tmp[n], tmp[i]  # 交换，将 tmp[i] 固定在第 n 位dfs(n + 1)                       # 开启固定第 n + 1 位字符tmp[i], tmp[n] = tmp[n], tmp[i]  # 恢复交换dfs(0)return res

剑指 Offer 39. 数组中出现次数超过一半的数字

题目

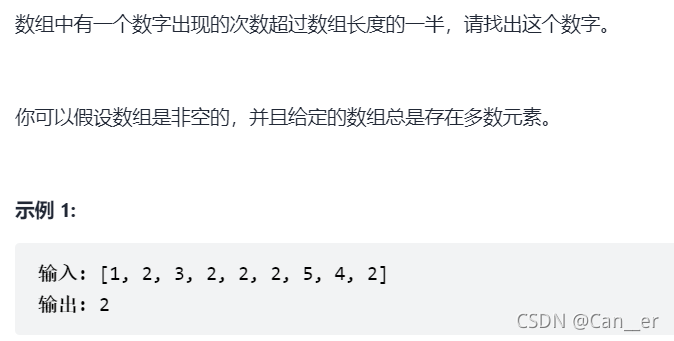
思路

这个题非常经典，且有很多思路将会写在这里，而下面给出的题解仅给出部分不常见思路的（后三种）。

• 哈希表：循环遍历数组，并将每个元素加入哈希映射，然后返回哈希映射中值最大的键
• 排序：当然可以使用那许多种排序算法啦，如果是自己编写堆排序，只需要 O(1) 即可（堆排序中的每个局部变量都会存在栈区，由编译器自动分配和释放，所以我们在空间复杂度中不予考虑），吐槽一句，python调库是真的快，不管是排序还是别的2333
• 随机化：大于1/2的概率都可以用随机化解决！
• 分治：二分后众数仍是至少一部分的众数
• Boyer-Moore投票算法（空间复杂度为O(1)）
  
  这个方法的原理较难证明，可以理解为：不同则抵消。当candidates是真正的众数时，count是真正的count，否则count和真正的count互为相反数。而因为count的值在变成0时就会更换candidates，故而count一定非负，所以最后一段中，count一定是真正的count（否则为负才能成为相反数），candidates也是真正的众数啦。

题解

• 随机化：

class Solution:def majorityElement(self, nums: List[int]) -> int:majority_count = len(nums) // 2while True:candidate = random.choice(nums)if sum(1 for elem in nums if elem == candidate) > majority_count:return candidate

• 分治：

class Solution:def majorityElement(self, nums: List[int]) -> int:def majority_element_rec(lo, hi) -> int:if lo == hi:return nums[lo]mid = (hi - lo) // 2 + loleft = majority_element_rec(lo, mid)right = majority_element_rec(mid + 1, hi)left_count = sum(1 for i in range(lo, hi + 1) if nums[i] == left)right_count = sum(1 for i in range(lo, hi + 1) if nums[i] == right)# 找出哪边含有众数return left if left_count > right_count else rightreturn majority_element_rec(0, len(nums) - 1)

• 投票法：

class Solution:def majorityElement(self, nums: List[int]) -> int:count = 0candidate = Nonefor num in nums:if count == 0:candidate = numcount += (1 if num == candidate else -1)return candidate

剑指 Offer 40. 最小的k个数

题目

思路

最容易想到的就是排序：这里介绍2种排序方法，系统的排序算法复习将在这篇文章中介绍，还没写，这里只介绍当前题中的应用

• 快排：快排实际上就是“哨兵划分”和“递归”的不断重复，哨兵划分的过程是双指针不断交换，接近的过程，递归的过程是对子问题的求解。看一个快排模板：

	def partition(i, j):while i < j:while i < j and arr[j] >= arr[l]: j -= 1while i < j and arr[i] <= arr[l]: i += 1arr[i], arr[j] = arr[j], arr[i]arr[l], arr[i] = arr[i], arr[l]return idef quick_sort(arr, l, r):i = partition(l, r)# 递归左（右）子数组执行哨兵划分quick_sort(arr, l, i - 1)quick_sort(arr, i + 1, r)

然后就会发现，诶这个题只需要返回前k个大的，并没有要求排好序的，所以只要划分到基准为第k+1个数字，那么前k个就已经划分出来啦

• 堆排序：维护一个k个大小的大顶堆，注意是k个大小，每次和堆顶比较，如果当前数字大于堆顶，则跳过，否则入堆，然后将堆顶（最大的元素）出堆，这样剩下的就是最小的k个啦。时间复杂度为 O(NlogK)。

题解

• 快排：

class Solution:def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:if k >= len(arr): return arrdef quick_sort(l, r):i, j = l, rwhile i < j:while i < j and arr[j] >= arr[l]: j -= 1while i < j and arr[i] <= arr[l]: i += 1arr[i], arr[j] = arr[j], arr[i]arr[l], arr[i] = arr[i], arr[l]# 快排的过程是对数组不断交换的过程，只需要排出前k个即可if k < i: return quick_sort(l, i - 1) if k > i: return quick_sort(i + 1, r)return arr[:k]return quick_sort(0, len(arr) - 1)

• 堆排序：

from heapq import *class Solution:def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:if k==0: return []Bheap = []for num in arr:if len(Bheap)<k:heappush(Bheap, -num)# 不能跟pop比较，会导致弹堆elif -num > Bheap[0]:heappushpop(Bheap, -num)else: continuereturn [-num for num in Bheap]

剑指 Offer 41. 数据流中的中位数（困难）

题目

思路

• 做出来很简单，但以最优的时空复杂度做出来比较难，中位数的问题无非是“排序”+取数，此时复杂度为*O(NlogN)*m。考虑维护两个堆，一个放大的数，一个放小的数，这样中位数可以直接取得。
  • 那么插入的顺序应该是，一个小，一个大…譬如我们规定，偶数时，取两个堆堆顶/2，再加入时往A堆加；奇数时候，A比B多一个，取A的堆顶，再加入时往B堆加。
  • 但是如何保证小的永远放到小的那边，大的放到大的那边呐？答案是：如果我要插入小的，我先放在大的堆中，然后把大的堆中最小的放到小的堆中。
• 另外，K神的题解中提到：Push item on the heap, then pop and return the smallest item from the heap. The combined action runs more efficiently than heappush() followed by a separate call to heappop().，所以中间逻辑可以合并，将更efficiently。

题解

class Solution:
# python中heapq中实现的是小顶堆，所以大顶堆需要取负！
from heapq import *class MedianFinder:def __init__(self):self.A = [] 	# 小顶堆，保存较大的一半self.B = [] 	# 大顶堆，保存较小的一半def addNum(self, num: int) -> None:if len(self.A) != len(self.B):heappush(self.A, num)heappush(self.B, -heappop(self.A))# 合并的写法：heappush(self.B, -heappushpop(self.A, num))else:heappush(self.B, -num)heappush(self.A, -heappop(self.B))# 合并的写法：heappush(self.A, -heappushpop(self.B, -num)def findMedian(self) -> float:return self.A[0] if len(self.A) != len(self.B) else (self.A[0] - self.B[0]) / 2.0

剑指 Offer 42. 连续子数组的最大和

题目

思路

• 动态规划：使用maxnum随时记录出现的最大值，sum累加直到sum一定不会给出正贡献，重新计数

题解

• 动态规划：

class Solution:def maxSubArray(self, nums: List[int]) -> int:sum = maxnum = nums[0]for _ in nums[1:]:# 只要sum是正，就是对最终的结果的正贡献，可以保留# 否则sum为负，还不如重新开始sum = sum + _ if sum>0 else _maxnum  = max(sum, maxnum)return maxnum

剑指 Offer 43. 1～n 整数中 1 出现的次数（困难）

题目

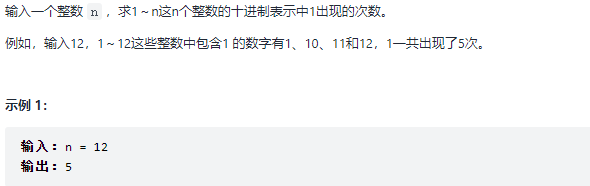
思路

属实是太难了，我不会，下面的题解是参照了评论区的用户 @细b，翻译出来的一个python版本，思路我大概一说：
先是决定整体使用递归，譬如1234和2345同样都是四位数，先算 最高位（这里是千位数） 贡献的1有多少个，最后进行递归234和345分别贡献了多少1即可

• 首先有一个规律：99以内一共20个，999内一共300个，9999内4000个，我们记这个数为base
• 最高位贡献的要分两种情况：
  • 千位是1：用999内贡献的300个，加上此时除去比1000多几个数就贡献几个（即1000 ~ 1234中的234个，但因为1000的没加，所以表达式应该是n-base+1）
  • 千位不是1：记千位为high，那几遍循环就已经贡献了high*base（2345中是2*99个），再加上以1开头的从 1000 ~ 1999的千位数一共1000个数（无论千位是2，3，4…都要加上这1000个），所以表达式为high*base + 1000
• 然后加上边界条件，和递归关系，上代码！

题解

class Solution:def countDigitOne(self, n: int) -> int:if n == 0: return 0if n < 10: return 1# 看这是个几位数digit = len(str(n))base = (digit-1)*pow(10, digit-2)# 当前的数量级，同时也是最高位非1需要加上的数exp = pow(10, digit-1)high = n//expif high == 1:return base + n + 1-exp + self.countDigitOne(n-high*exp)else:return base*high + exp + self.countDigitOne(n-high*exp)

剑指 Offer 44. 数字序列中某一位的数字（中等）

题目

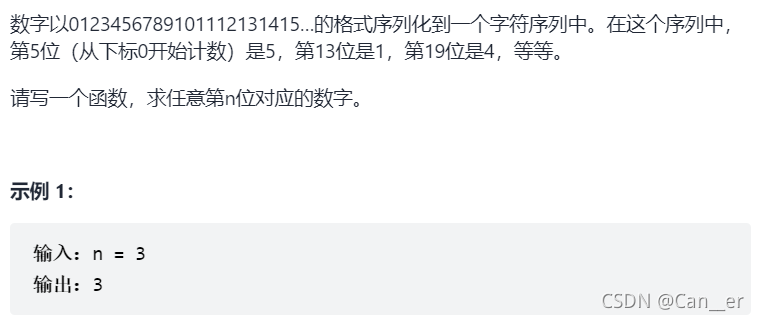
思路

找规律的问题呀，记住就好了，把问题拆解为以下三步：

• 求这是个几位数
• 求这是几位数中离最小的那个多远的距离，通过距离//位数得出这个数字
• 求这个位置是这个数字中的第几个数字

举个例子：

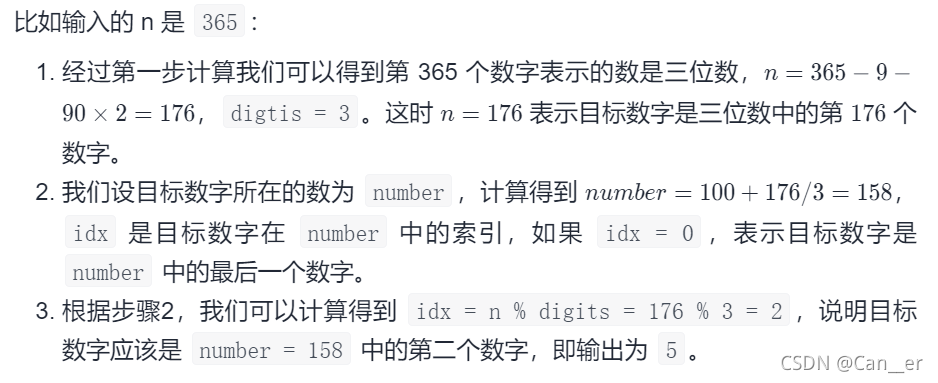
题解

class Solution:def findNthDigit(self, n: int) -> int:# 一位数占9位，二位数占10*2*（10-1）位，三位数占10*3*10*（10-1）位# n位数占9*10^(n-1)*n位digit, exp, count = 1, 1, 9while n > count:n -= countexp *= 10digit += 1count = 9 * exp * digitstart = exp# 因为减去的数是以9为结尾，所以这里需要n-1，才是以0开头所剩下的距离num = start + (n-1) // digitreturn int(str(num)[(n-1) % digit])

剑指 Offer 45. 把数组排成最小的数（中等）

题目

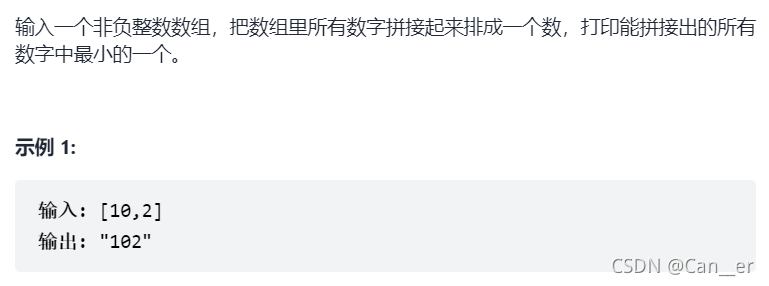
思路

• 贪心算法：将较小的数放到前面即可。但是这个较小的界定应该是，逐位比较，返回按位小的，再一看题，其实规则已经给我们了，即
  
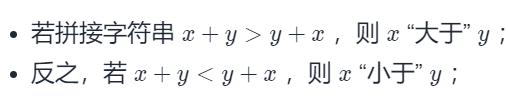
  剩下的问题就是自定义排序即可，定义完成后套用任何排序（快排，冒泡…）都可以

题解

• 若干排序算法将在以后做总结：算法复习，还没写
• 调库，定义规则，内置函数的时间复杂度为O(NlogN)

class Solution:def minNumber(self, nums: List[int]) -> str:def sort_rule(x, y):str1, str2 = x + y, y + xif str1 > str2: return 1elif str1 < str2: return -1else: return 0strs = [str(num) for num in nums]strs.sort(key = functools.cmp_to_key(sort_rule))return ''.join(strs)

剑指 Offer 46. 把数字翻译成字符串（中等）

题目

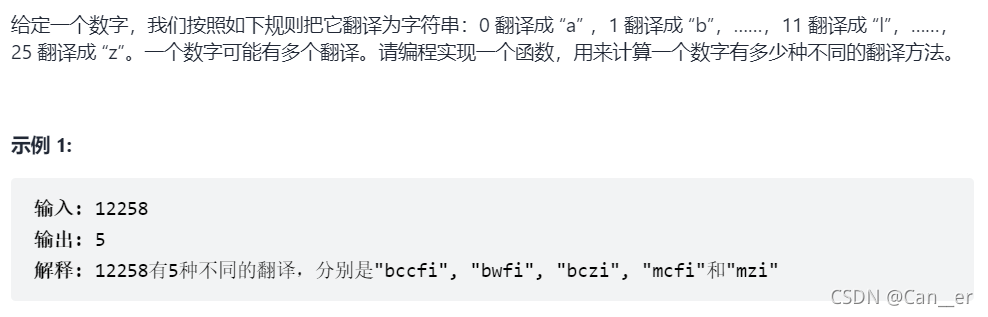
分析

• 递归即可，这里选择从后向前开始考察（从前向后也是一样的，只不过取余不太方便）：
  • 边界条件：如果数字在0 ~ 10，返回1即可
  • 递归关系：倒数第一位和倒数第二位可以组成10~25，则这两位有两种组合情况，组合or单个，对应剩下的是num//100和num/10 ，其实特别像那个青蛙跳台阶问题，并不是直接累加组合，而是分类，分类进行子问题的划分，因为这两题的公共点在于不是选or不选，而是选Aor选B，将选A和选B的两种情况加起来就是当前这一步能选的总情况。如果倒数第一位和倒数第二位不可以组成10 ~ 25之间的数，那递归就只有num/10，譬如9999，只有一种划分情况。
• 动态规划：在递归的子问题很明确的情况下，递归的“归”即是动态规划！且动态规划中，只用到了i-1和i-2，那就可以用三个（甚至两个）变量直接取代，进一步简化。下面这个图可以很好的帮助理解，初始化dp[len(num)]为1是为了倒数第二个字符可能出现两种情况。
  

题解

• 递归：

class Solution:def translateNum(self, num) :if num < 10 : return 1if 10 <= num % 100 <= 25 :return self.translateNum(num // 10) + self.translateNum(num // 100)else :return self.translateNum(num // 10)

• 动态规划：

class Solution:def translateNum(self, num: int) -> int:fstnum = secnum = 1# y是个位，x是十位y = num % 10while num != 0:num //= 10x = num % 10fstnum, secnum = (fstnum + secnum if 10 <= 10 * x + y <= 25 else fstnum), fstnumy = xreturn fstnum

剑指 Offer 47. 礼物的最大价值（中等）

题目

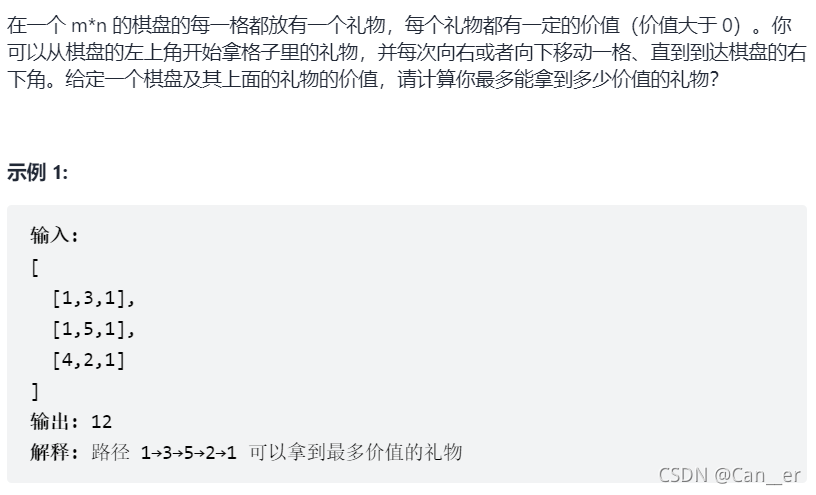
思路

• 来吧，动态规划，记录当前的价值，无论如何结束点在最后，因为不管走到哪里，可以继续向下（右）累加
• 动态规划一般有两点可以改进：
  • 当 grid矩阵很大时，i=0 或 j = 0的情况仅占极少数，相当循环每轮都冗余了一次判断。因此，可先初始化矩阵第一行和第一列，再开始遍历递推。
  • 或者一种常用的方法，多开一行一列的空间，初始化为0，遍历时从1开始，下标使用dp[i-1][j-1]，无须判断边界即可，这个题中如果使用原地覆盖则无法多开空间啦，否则会覆盖。
  • 覆盖遍历！如果无须返回使用grid中的数据（仅使用了dp[i-1][j]，dp[i][j-1]，dp[i][j]），可以直接原地覆盖。

题解

• 我写的代码：

class Solution:def maxValue(self, grid: List[List[int]]) -> int:dp = []INF = float("-inf")for row in range(0,len(grid)):dp.append([INF]*len(grid[0]))dp[0][0] = grid[0][0]for row in range(0,len(grid)):for col in range(0,len(grid[0])):dp[row][col] = max(dp[row][col-1]+grid[row][col] if col!=0 else INF, dp[row-1][col]+grid[row][col] if row!=0 else INF, grid[row][col])return dp[-1][-1]

• 原地覆盖+初始化一行一列版（还是K神的）：

class Solution:def maxValue(self, grid: List[List[int]]) -> int:m, n = len(grid), len(grid[0])for j in range(1, n): # 初始化第一行grid[0][j] += grid[0][j - 1]for i in range(1, m): # 初始化第一列grid[i][0] += grid[i - 1][0]for i in range(1, m):for j in range(1, n):grid[i][j] += max(grid[i][j - 1], grid[i - 1][j])return grid[-1][-1]作者：jyd
链接：https://leetcode-cn.com/problems/li-wu-de-zui-da-jie-zhi-lcof/solution/mian-shi-ti-47-li-wu-de-zui-da-jie-zhi-dong-tai-gu/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

剑指 Offer 48. 最长不含重复字符的子字符串（中等）

题目

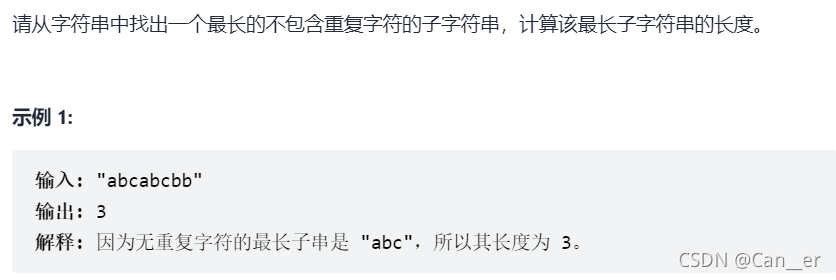
思路

• 动态规划+线性遍历：向右遍历直到停止即可，不再给出题解，比较常规的o(n^2)。
• 动态规划+哈希表：
  • 没必要二维的记录，只需要将“重复元素”之前的元素从字典中剔除即可，就相当于重新计数（这里的重新并不是遇见重复的就从1开始，而是从index-之前的index，因为中间的元素也不同）啦
  • 还有一点，因为只需要返回最大值的长度而不是具体子串，我们可以直接省去动态规划的数组，使用一个变量记载！
• 滑动窗口：本质上和第二个方法是一样滴，只不过更直观的用一个左边界来限定

题解

• 动态规划+哈希：

class Solution:def lengthOfLongestSubstring(self, s: str) -> int:chardict = dict()cnt, maxcnt  = 0,0for index in range(0,len(s)):if s[index] in chardict and cnt >= index - chardict[s[index]]:cnt = index - chardict[s[index]]# 便于理解，如果出现重复字符，那么（第一个）重复字符之前的需要取消记录# 实际上与上文的判断 “当前累计的长度” 和 “重复元素是否在区间内” 是一个作用# for key,value in list(chardict.items()):# if value<chardict[s[index]]:# chardict.pop(key)else:cnt += 1chardict[s[index]] = index    maxcnt = max(cnt,maxcnt)return maxcnt

• 看看K神的动态规划，直接取消分支，反正取不到是+1嘛，那我就返回默认值-1就好了：

class Solution:def lengthOfLongestSubstring(self, s: str) -> int:dic = {}res = tmp = 0for j in range(len(s)):i = dic.get(s[j], -1) # 获取索引 idic[s[j]] = j # 更新哈希表tmp = tmp + 1 if tmp < j - i else j - i # dp[j - 1] -> dp[j]res = max(res, tmp) # max(dp[j - 1], dp[j])return res作者：jyd
链接：https://leetcode-cn.com/problems/zui-chang-bu-han-zhong-fu-zi-fu-de-zi-zi-fu-chuan-lcof/solution/mian-shi-ti-48-zui-chang-bu-han-zhong-fu-zi-fu-d-9/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

• 滑动窗口：

class Solution:def lengthOfLongestSubstring(self, s: str) -> int:dic, res, left = {}, 0, -1for right in range(len(s)):if s[right] in dic:# 如果当前左指针已经在重复元素之后，那就没必要更新left = max(dic[s[right]], left) dic[s[right]] = right res = max(res, right - left) return res