RC522线圈设计及相关参数的选定

LC低通滤波电路（蓝色区域）

TX1、TX2为载波发送引脚。

载波或者载频（载波频率）是一个物理概念，是一个特定频率的无线电波，单位[Hz]，是一种在频率、幅度或相位方面被调制以传输语言、音频、图象或其它信号的电磁波。

下图为TX1、TX2引脚发送的波形

可以看到TX1、TX2发送的载波为幅值相等，频率为13.56MHz左右,相位相差180°的正弦信号，

经过后续电路在线圈内叠加产生大于2倍幅值的正弦波(串联谐振增益)。

这个频率要用一个石英振荡器发生 但它同时也产生高次谐波 为了符合国际 EMC 规定 13.56MHz 中的三次 五次和高次谐波要被良好地抑制 。

所以这里采用的是低通滤波器来滤除13.56MHz的谐波。

这个低通滤波器第一时间我想到的是RC低通，但是官方使用的是LC低通滤波，

我手里的PCB不方便进行实验，于是就是用Multism进行了仿真

LC和RC的截止频率均为13.56MHz左右，

上为LC低通滤波波特图

下为RC低通滤波波特图

根据波特图可以看出LC低通滤波其波形并不是正常的低通滤波，而是在谐振频率点发生了谐振对信号产生了增益的作用，

而RC低通滤波在截止频率下不仅没有对信号产生增益，反而抑制了信号

手册里采用的LC低通截止频率附近会对TX发出载波产生谐振增益，这个增益有助于提升NFC的刷卡距离

那这个增益能不能通过修改LC的值进行增大呢？

根据LC谐振频率公式：
$$\omega =\frac{1}{\sqrt{LC}}$$
LC低通滤波传递函数：
$$Av=\frac{1}{1-{\omega }^{2}LC}$$
可得
$$Av=\frac{1}{1-1}=+\infty$$
也就是说当在谐振频率处的 $Av$ 是趋于无穷大的

由于我选取的$LC$谐振频率只是接近于$13.56MHz$,并且信号源输出的频率为标准的$13.56MHz$,所以仿真的波特图$Av$不会趋于无穷大

但是我们可以确定的一点是，我们选取得$LC$谐振频率越接近于$13.56MHz$，$Av$就越大。

而且$Av$与$C$后所带的阻抗有关

负载阻值越高，增益越大。

这里$LC$的选取只要接近$13.56MHZ$就可以了，越接近效果越好。

NFC天线电路(绿色区域)

NFC天线本身就是一个线圈，本就含有电感$L$，导线包含电阻$R$,相邻导线之间存在电容$C$,

所以我们可以将线圈进行简化，调节谐振频率时，由于电容$C2$非常小，可以忽略不计

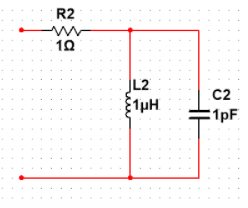
通过等效电路可以方便我们的参数选定，线圈的电感值不好测定，我使用的是ST官方提供的计算工具

NFC电感在线计算

不过由于我画的线圈并不是规则的矩形，这种方法对我来说基本没有办法用，而且实验室也没有测量电感的仪器

本来想着谐振法测电感利用公式
$$\omega =\frac{1}{\sqrt{LC}}$$
和波形发生器、示波器进行测试，找到谐振频率就能倒推$L$的值

但是由于线圈的$L$特别小属于$nH$级别，谐振频率$f$基本已经达到100MHZ以上了，

基本已经超出示波器和波形发生器测试范围了，

这种方法基本也不能用(但凡有台测电感的仪器,我都不会写这一部分┐(─__─)┌)

后来又想到串联一个电阻和电感，利用波形发生器产生不同频率的正弦波，

加到这个串联回路上就能根据感抗$X_L=\omega \ast L$上分压来测量电感了

电路如下，非常简单，利用分压就可以算出$L$

由于$L$很小，我直接从$20MHZ$开始测试

去掉突变项，取一个近似值$0.0000005H$左右

再次通过公式
$$\omega =\frac{1}{\sqrt{LC}}$$
计算得到$C\approx 276PF$

由于计算和测量存在误差最后实际测试$C=330PF$时效果最好

实测距离$40-50mm$左右

匹配电路(黄色区域)

此部分主要是调整整个天线发射部分的谐振频率点到$13.56MHz$附近，这样可以使得线圈上的信号幅度增加有利于磁场辐射。

另外匹配电路还要将发射部分电路的电阻匹配到与读卡芯片的输出电阻附近，典型的是50欧姆（不同芯片不一样）。

这样可以使得天线部分获得最大功率有利于读卡距离提升。

阻抗匹配（impedance matching） 主要用于传输线上，以此来达到所有高频、微波信号均能传递至负载点的目的，而且几乎不会有信号反射回来源点，从而提升能源效益。信号源内阻与所接传输线的特性阻抗大小相等且相位相同，或传输线的特性阻抗与所接负载阻抗的大小相等且相位相同，分别称为传输线的输入端或输出端处于阻抗匹配状态，简称为阻抗匹配。

负载阻抗等于信源内阻抗，即它们的模与辐角分别相等，这时在负载阻抗上可以得到无失真的电压传输。

这个我理解的意思就是从匹配电路和线圈，总阻抗为50欧姆

品质因子

假设天线电感 L 和电阻 R 的值已知
天线的品质因子是天线正确调谐和所获得的性能的一个重要特性 天线的品质因子由下面的公式定义
$$Q=\frac{\omega \ast L}{R}$$
这个公式从能量角度理解为产生磁场的无功功率与电阻上消耗的有功功率的比值。

线圈作为通信媒介，我们肯定是希望产生磁场的无功功率更大一些，也就是$Q$更大一些。

根据天线的几何形状 Q 的值通常在 50-100 之间 要进行正确的数据传输这个值还要减少

由于RFID通信方式最小脉宽也要$T=3us$

带宽
$$B=\frac{f}{Q}$$

时间与带宽的乘积规定：
$$B\ast T\ge 1$$

算出品质因子的要求为
$$Q\le f\ast T\le 40.68$$
周立功的手册里推荐Q问为35左右

我们已知线圈$L$和$R$

利用上述公式
$$R_Q=\frac{\omega \ast L}{Q}-R$$
$R_Q$为外接电阻，用来改善线圈品质因数，

我计算的$R_Q\approx 0.2\Omega$，由于没有这么小的电阻，直接使用$0\Omega$电阻代替了

其实这个$R_Q$可以取稍微大一些，因为$R_Q$大一些的话，品质因数$Q\le 35$

在低于40下基本都是可以正常工作的。

阻抗匹配

这里我们直接看匹配电路和线圈，在$13.56MHZ$下使其阻抗达到50Ω

其他参数选取基本完成了，现在只剩下$C26$一个未知项

这里的计算属实麻烦，我直接在推荐电路数值周围改了改，取了一个较为合适的值。

(这个计算公式实在看不懂# -__-)

接收电路（浅黄色区域）

先看引脚功能

VMID为RX提供参考电压，RX负责接收信号

为了减少干扰 在 VMID 管脚连接一个电容到地

这一部分我是直接参考官方的推荐电路，因为线圈参数确定的话，传回来的信号频率基本也是确定的。

TGND的疑问

在线圈中间引出一条地线，实际上把线圈分成了两个回路

$TX1->TGND$

$TX2->TGND$

$TX1、TX2$输出的为差分信号，所以这两条回路在任意时刻流过的电流方向都是相同的

所以产生的磁场会进行叠加。

若果我们去掉红框部分的$TGND$

回路变成了$TX1->TX2$,并且因为$TX1、TX2$为差分信号，

也就是$TX1、TX2$的信号进行了叠加。

实测接$TGND$与不接$TGND$效果相差无几。

参考资料：
设计 MF RC500 的匹配电路和天线的应用指南

13.56MHz RFID读写器天线匹配设计方法

13.56Mhz下50欧姆阻抗匹配简易教程