本文主要是介绍有3扇门,其中1扇门后有汽车,另两扇门后为山羊。你选择第1扇门后,主持人打开第2扇门,见到山羊。问你这时该不该换选第3扇门?,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
有3扇门,其中1扇门后有汽车,另两扇门后为山羊。你选择第1扇门后,主持人打开第2扇门,见到山羊。问你这时该不该换选第3扇门?
这个问题要分两种情况讨论:主持人知道每扇门后面是什么,以及主持人不知道每扇门后面是什么。
用A,B,C表示三扇门;S表示汽车的实际位置,S可以取A,B,C;X表示我选择的门,已知X=A;Y表示主持人选的门,在主持人做决策时,Y可选B和C。
假设最初汽车放在三扇门后面的概率是相同的,即P(S=A)=P(S=B)=P(S=C)=1/3。
1. 主持人不知道每扇门后面是什么
假设主持人不知道每扇门后面是什么,那么,当X=A后:
P(Y=B|S=A)=0.5
P(Y=C|S=A)=0.5
P(Y=B|S=C)=0.5
P(Y=C|S=C)=0.5
因此,当已知Y=B,S≠B后:
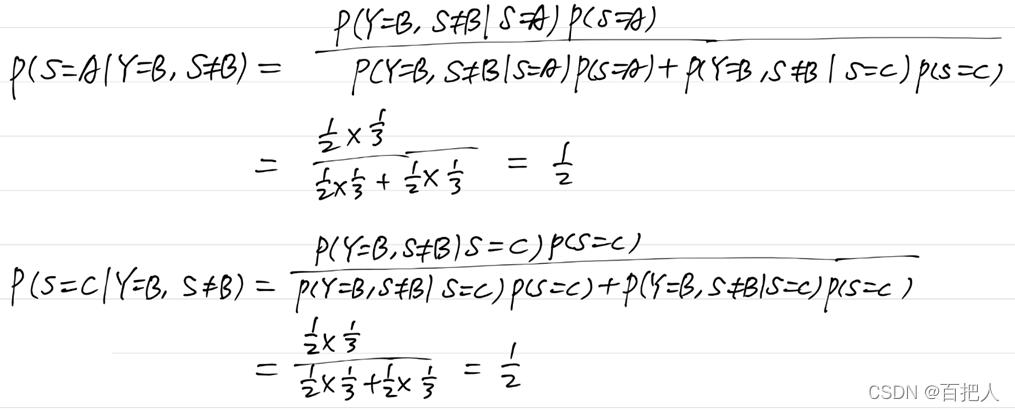
因此汽车在第一扇门和第三扇门后面的概率是相等的,换不换都可以。
2. 主持人知道每扇门后面是什么
假设主持人知道每扇门后面是什么,并且保证不会打开后面有汽车的门。那么:
P(Y=B|S=A)=0.5
P(Y=C|S=A)=0.5
P(Y=B|S=C)=1
P(Y=C|S=C)=0
因此,当已知Y=B,S≠B后:
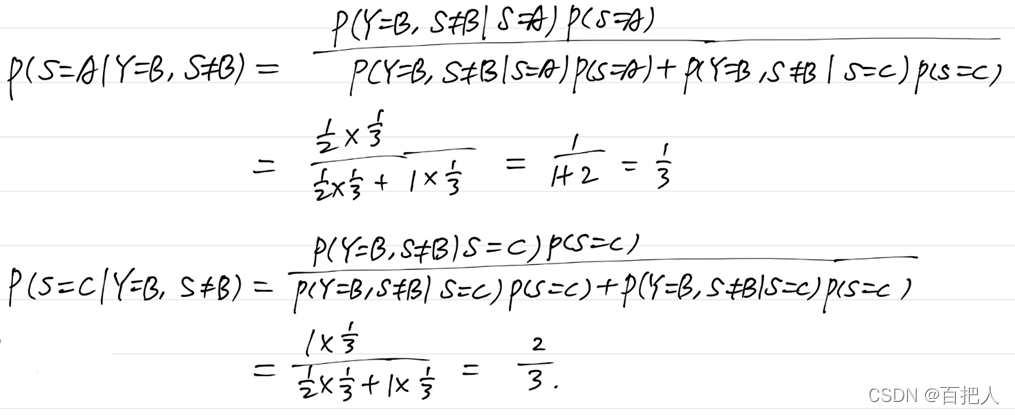
显然P(S=A|Y=B,S≠B)<P(S=C|Y=B,S≠B),汽车在第一扇门后面的概率比在第三扇门后面大,因此应该换选第三扇门。
这篇关于有3扇门,其中1扇门后有汽车,另两扇门后为山羊。你选择第1扇门后,主持人打开第2扇门,见到山羊。问你这时该不该换选第3扇门?的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







