第六十四天学习记录：三条单身狗。数组里大多数都是成对的，只有三个数出现一次，找出这三条狗doge

以下前序可不看……

抛出这个问题的原因是在学习C语言视频课程的最后一节课临近结尾时，老师在讲解作业时有一道题是如下图：

因为时间原因，老师讲得比较急，给出了一个思路。但最终还是处于半懂状态。而在解题过程中，老师还提了一句还有“找出三个数字是出现一次”的情况。

虽然学习完一套视频课程是一件让人愉悦的事情，但是对这一道题的一知半解始终在心中是一个疙瘩。。虽然实际情况C语言还有很多未知的奥秘等待着去探索，外加之前学习的内容存在遗忘的情况。
但本着个人的一个准则……对于所学知识，我可以容忍学会后忘记（后面补起来相对容易），也容忍很多很多没有遇到的问题……但是不能容忍遇到了却没弄明白的问题。
废话不多说，本文通过C语言，将从最简单的一条单身狗开始，由易到难解答问题。

正题开始

为了方便书写，我们尽量采用小于16的数字来举例并且忽略int类型的前28位。

一条单身狗

数组里大多数都是成对的，只有一个数出现一次，找出这一个数字。
这也是最简单的，用异或运算将数组里的所有数字都异或一遍即求出那个只出现一次的数字。
原因是基于异或运算的特性。如果是两个相同的数字异或，其值为0。

因此，不论这个数组里有多少成双成对的数字，一旦全部异或一遍，最终的值都是0.
再来看异或的另一个特性：
当一个数字和0异或后得到的是这个数字本身。
于是最后0再和这最后一个数字异或后还是得到这个数字本身，因此这个数字就是那个唯一的单身狗，代码如下：

#include <stdio.h>int findoneSingledog(int arr[], int n) {int result = 0;for (int i = 0; i < n; i++) {result ^= arr[i];}return result;
}int main()
{int arr[9] = { 1,1,2,5,2,3,3,4,4};printf("%d\n", findoneSingledog(arr, 9));return 0;
}

输出：5

两条单身狗

首先，引出一个优雅的函数Lowestbit，它的作用是求一个整数最低为1的比特位，并返回带有这唯一一个为1的比特位的值。0返回0。

int Lowestbit(int num)
{return num&(-num);
}

举个例子，3的二进制是0011，最低为1的比特位就是第一位，返回0001. 十进制是1
12的二进制是，1100，最低的比特位是第三位，返回0100. 十进制是4
他们的特点是32位中有且只有1位是1

了解了这个函数之后，再来了解一个事实：
两个不一样的数，他们异或之后，必定会至少有一个位是不一样的。
比如5-二进制0101和6-二进制0110，他们的第一位和第二位不一样。
比如5-二进制0101和7-二进制0111，他们的第二位不一样。
因此，如果将这两个数异或之后得到一个数xorResult。
我们再将xorResult带入刚刚的函数Lowestbit
Lowestbit(xorResult),返回的整型数32位只有1位是1，而这两条单身狗在这一位位置的数必定有一个是1，有一个是0.根据这个特性，可以将数组分为2组。而这两条单身狗也必然会被分开。
比如拿5和7举例。
0101和0111异或后的xorResult=0010，带入函数Lowestbit返回0010，1的位置在第二位。
0101的第二位是0，0111的第二位是1

在将两单身狗分到各自的组后就简单了，用前面“一条单身狗”的方法即可求出。
代码如下：

#include <stdio.h>int Lowestbit(int num)
{return num&(-num);
}void findTwoSingledog(int arr[], int n, int* num1, int* num2)
{int a = 0;int b = 0;int i = 0;int xorResult = 0;for (i = 0; i < n; i++) {xorResult ^= arr[i];}for (i = 0; i < n; i++){if ((arr[i] & Lowestbit(xorResult)) == 0) {a ^= arr[i];}else {b ^= arr[i];}}*num1 = a;*num2 = b;
}int main()
{int a = 0;int b = 0;int arr[10] = { 1,1,6,2,5,2,3,3,4,4 };findTwoSingledog(arr, 10, &a, &b);printf("%d %d\n", a, b);return 0;
}

输出：6，5

三条单身狗

在掌握了一条二条之后，我们迎来了相对前面两种情况更难的一种。
因为两条单身狗还可以通过异位0和1分到2组。而三条狗的话二组也分不下……
这个时候，就需要另辟蹊径了。
如何另辟蹊径呢？我们可以通过某种方式强制性让两条单身狗在一起。
我们可以先随便举个例子：
4-二进制：0100–狗1
6-二进制：0110–狗2
12-二进制：1100–狗3
通过这个个例，我们观察到狗2身上有个特性和狗1，狗3不一样，狗2最低位数为1的位是2，而狗1，狗3都在第三位。那我们将数组中所有的数穿一件“衣服”，这件衣服叫**“Lowestbit”**，这三个数就成了：
Lowestbit（狗1）= 0 1 0 0
Lowestbit（狗2）= 0 0 1 0
Lowestbit（狗3）= 0 1 0 0

该成双成对的穿上Lowestbit后，或许会出现一些相同的情况，但最终，他们还是会一一配对。毕竟只要是偶数个相同的数异或其值都是0.
而此时，Lowestbit（狗1）和Lowestbit（狗3）也成功配对，最后就剩下了：
Lowestbit（狗2）= 0 0 1 0，因此，我们加一个条件限制“0 0 1 0”让所有船上Lowestbit等于0 0 1 0的数聚集在一起。那么狗2将会从狗1和狗3中单独出来，而这一堆聚集的其他数同样可以全部配对成功，剩下狗2
于是狗2被找出来了。
下面就简单了，知道了狗2的值后，我们往这群数字中加入一个虚拟的狗2，那么狗2就和虚拟狗2配对成功，剩下狗1和狗3.要找这俩是不是就可以用前面找“两条单身狗”的方法了。于是3条狗就被找出来了。大功告成？
还没完呢！！！
刚刚说了是随便举个例子。随便不能代表全部。我们还应该考虑一些极端情况。
比如：
2-二进制：0010–狗1
6-二进制：0110–狗2
10-二进制：1010–狗3
这种情况下，即便是穿上Lowestbit，这哥仨的属性都是0010，如果将0010作为限制条件，这哥仨还是会被聚集在一起。
再或者：
1-二进制：0001–狗1
2-二进制：0010–狗2
4-二进制：0100–狗3
这种情况下，即便是穿上Lowestbit，这哥仨的属性都还是不一样。不过这种情况下倒也简单，将穿上Lowestbit的所有数字异或之后得出的值0111再Lowestbit之后得到0001，用0001作为限制条件也能够找出狗1
所以我们还是应该关注第一种极端情况。
造成第一种极端情况的根本原因是什么呢？
是他们三个最低位为1的位数都是一样的。这就意味着这三个数有一个特性，是他们三个必定有一个相同的位都是1。那么就可以知道这种情况下，他们3个异或之后的结果不可能是0.
那这就意味着，如果能够通过某种方式让这3个数异或之后必定为0，就可以保证一定能找出一个属性与另外二个不一样的狗。因为如果3个数异或后是0，就可以说他们三个在相同位数上的二进制只有两种情况，第一种是都为0，第二种是两个为1，一个为0.首先我们排除他们所有位都是0的可能性，那我们就肯定能够通过Lowestbit找出这一个位置，这个位置有两个1，一个0.
那下一步该怎么办？
我们所具备的资源并不多，不如就先将所有的数字异或一遍吧……
异或后得出TdogxorResult，TdogxorResult就相当于是三条狗异或得出的值。

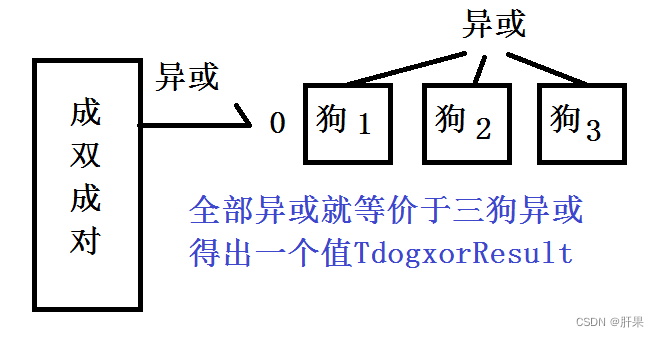
首先，TdogxorResult如果是0，就很简单。前面说的如果三狗异或是0，必然可以通过前面的方法找出特性不一样的那一条。
那么TdogxorResult如果不为0呢？
我们再用TdogxorResult与狗1，狗2，狗3异或。发现这4个数异或之后就必定是0。
那么我们用三个TdogxorResult和三条狗一共6个数异或之后的结果也是0
这意味着我们又有一件新衣服“TdogxorResult^”
（TdogxorResult^狗1）

（TdogxorResult^狗1）^（TdogxorResult^狗2）^（TdogxorResult^狗3）=0

就是说，我们将所有数字先穿上TdogxorResult^之后，就能保证狗仨必满足有一条特性异禀。
然后再将所有数字套上Lowestbit之后：

Lowestbit（TdogxorResult^狗1）
Lowestbit（TdogxorResult^狗2）
Lowestbit（TdogxorResult^狗3）

这样看上去是不是觉得单身狗的B格瞬间提升了许多。

根据以上的思路，我们就可以写代码了：

#include <stdio.h>int Lowestbit(int num)
{return num&(-num);
}void findTwoSingledog(int arr[], int n, int* num1, int* num2)
{int a = 0;int b = 0;int i = 0;int xorResult = 0;for (i = 0; i < n; i++){xorResult ^= arr[i];}for (i = 0; i < n; i++){if ((arr[i] & Lowestbit(xorResult)) == 0){a ^= arr[i];}else {b ^= arr[i];}}*num1 = a;*num2 = b;
}void findThreeSingledog(int arr[],int newarr[], int n, int* num1, int* num2, int* num3)
{int TdogxorResult = 0;int keynum = 0;int i = 0;int a = 0;//假设a对应num1是第一条狗int b = 0;int c = 0;for (int i = 0; i < n; i++){TdogxorResult ^= arr[i];//得出所有数字异或后的结果}for (int i = 0; i < n; i++) {keynum ^= Lowestbit(TdogxorResult ^arr[i]);//得出关键限值条件}for (int i = 0; i < n; i++){if (Lowestbit(TdogxorResult ^arr[i]) == keynum){a ^= arr[i];//通过限值条件筛选出的一条狗}}newarr[n] = a;//这里懒得用可变数组，这句话的意思可以理解成给原数组加入一个和第一条狗一模一样的虚拟狗//这样newarr就只有2条不能配对的狗了……findTwoSingledog(newarr, 12, &b, &c);*num1 = a;*num2 = b;*num3 = c;
}int main()
{int a = 0;int b = 0;int c = 0;int arr[11] = { 1,1,6,2,5,2,3,3,4,7,4 };int newarr[12] = { 1,1,6,2,5,2,3,3,4,7,4,0 };//这里就懒得用可变数组了……findThreeSingledog(arr, newarr,11, &a, &b, &c);printf("%d %d %d\n", a, b, c);return 0;
}

输出：

改成极端情况：
int arr[11] = { 1,1,4,4,6,2,3,3,9,10,9 };

int arr[11] = { 1,10,4,6,6,2,3,3,9,10,9 };

感谢观看……