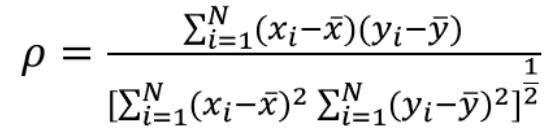2021SC@SDUSC-山东大学软件工程与实践-Senta(八)

本期续接2021SC@SDUSC-山东大学软件工程与实践-Senta(七)，继续对Metrics
中的glue_eval进行分析。

def matthews_corrcoef(preds, labels):"""matthews_corrcoef"""preds = np.array(preds)labels = np.array(labels)tp = np.sum((labels == 1) & (preds == 1))tn = np.sum((labels == 0) & (preds == 0))fp = np.sum((labels == 0) & (preds == 1))fn = np.sum((labels == 1) & (preds == 0))mcc = ( (tp * tn) - (fp * fn)) / np.sqrt((tp + fp) * (tp + fn) * (tn + fp) * (tn + fn) )return mcc

构建matthews_corrcoef函数进行二分类评估：运用numpy中的array函数创建preds 和 labels两个数组，并计算mcc指标。

MCC是应用在机器学习中，用以测量二分类的分类性能的指标，该指标考虑了真阳性，真阴性，假阳性和假阴性，通常认为该指标是一个比较均衡的指标，即使是在两类别的样本含量差别很大时，也可以应用它。
MCC本质上是一个描述实际分类与预测分类之间的相关系数，它的取值范围为[-1,1]，取值为1时表示对受试对象的完美预测，取值为0时表示预测的结果还不如随机预测的结果，-1是指预测分类和实际分类完全不一致。

def f1_score(preds, labels):"""f1_score"""preds = np.array(preds)labels = np.array(labels)tp = np.sum((labels == 1) & (preds == 1))tn = np.sum((labels == 0) & (preds == 0))fp = np.sum((labels == 0) & (preds == 1))fn = np.sum((labels == 1) & (preds == 0))p = tp / (tp + fp)r = tp / (tp + fn)f1 = (2 * p * r) / (p + r + 1e-8)return f1

构建f1_score()函数计算f1指标。 f1: 精确率和召回率的调和平均。

def pearson_and_spearman(preds, labels):"""pearson_and_spearman"""preds = np.array(preds)labels = np.array(labels)pearson_corr = pearsonr(preds, labels)[0]spearman_corr = spearmanr(preds, labels)[0]return {"pearson": pearson_corr,"spearmanr": spearman_corr,"corr": (pearson_corr + spearman_corr) / 2,}

构建pearson_and_spearman函数计算pearson和spearman统计系数

pearson系数用于评估两个连续变量之间的线性关系。

-1 ≤ p ≤ 1
p接近0代表无相关性
p接近1或-1代表强相关性

spearman系数评估两个连续变量之间的单调关系。在单调关系中，变量趋于一起变化，但不一定以恒定速率变化。

def acc_and_f1(preds, labels):"""acc_and_f1"""preds = np.array(preds)labels = np.array(labels)acc = simple_accuracy(preds, labels)f1 = f1_score(preds, labels)return {"acc": acc,"f1": f1,"acc_and_f1": (acc + f1) / 2,}

构建acc_and_f1函数求acc与f1的平均值。
ACC = (TP + TN) / (P + N) 即：(真阳性+真阴性) / 总样本数