树的直径（两次最远法）

本文主要是介绍树的直径（两次最远法），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

原题链接

树中的最长路径称为树的直径。
一棵树可以有多条直径，他们的长度相等。

两次最远法

步骤：

• 任取一个结点$u$，找出树中距$u$最远的结点，记为$v$
• 再以$v$作为起点，找出树中距$v$最远的结点，记为$w$
• 则$v,w$之间的距离即树的直径

显然，如果$v$是直径的一端，那么距其最远的结点$w$ 一定是直径的另一端。
我们只需证明：以任意结点作为起点，所找到的距其最远的点是直径的一个端点。

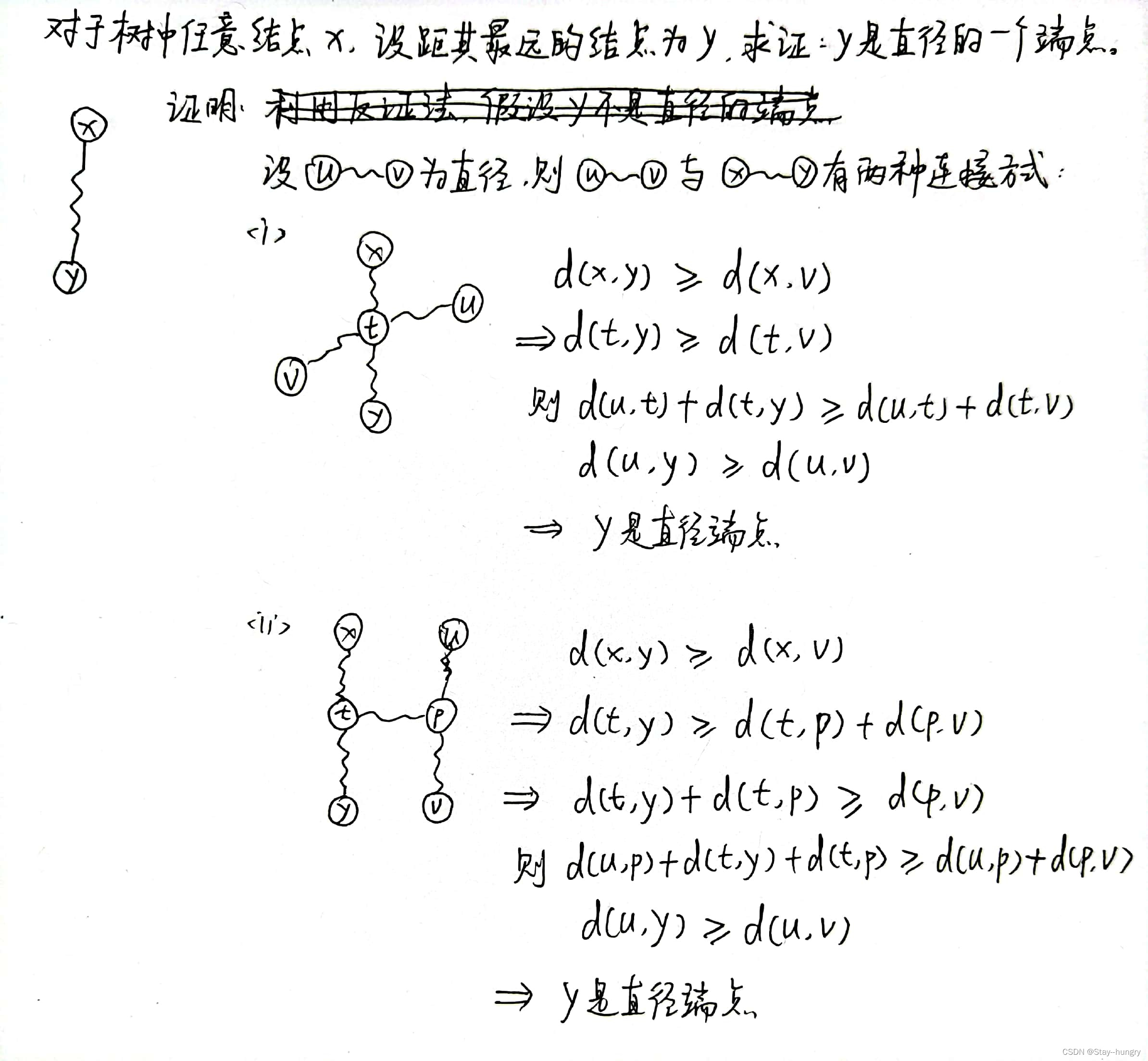
若树中存在负权边，则无法用该方法求直径。
扩展阅读

DFS实现

由于树中任意一点到其余所有点的路径都是唯一的，即任意一点到其余所有点的距离都是固定的，因此可以以某一个点作为起点进行DFS，如此便可求出其余所有点到该点的距离。

struct Edge
{int ne, w;
};
vector<Edge> h[N];void dfs(int u, int d) //搜索到了结点u
{dist[u] = d;st[u] = true;for (auto edge :

这篇关于树的直径（两次最远法）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---