铁人两项
求出三元组(s,c,f)的个数,使得在图中从s到c到f有一条简单路径。
考虑如果是树的话怎么做。若选出两点s和f的话,三元组的个数就要加上s和f之间的所有点。那么,换个思路,我们可以考虑每个点被统计到的次数(难道这就是所谓转换法吗?!)。那么一个树形dp就解决了。
但是,这是个图,怎么办呢?我们发现我们可以直接把点双缩起来,然后把某个点双的值改为点双中的点数。但是,别忘记点双不能缩点。因此我们只能用圆方树。把方点的值变成点双中点的个数,圆点的值变成-1,那么就可以愉快的对圆方树统计了。具体证明……我也不会啊&……&
注意圆方树的某种情况:
while (st[tl+1]!=v){ //不能写成st[tl]!=u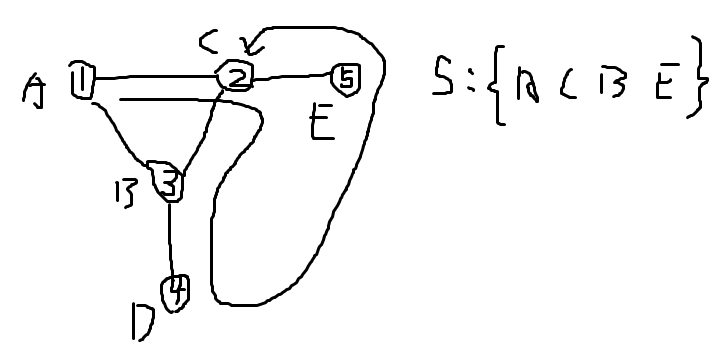
#include <cstdio>
#include <algorithm>
using namespace std;const int maxn=2e5+5, maxm=2e5+5;
int n, m;
struct Edge{int fr, to, nxt;
}e1[maxm*2], e2[maxm*2];
int cnte1, cnte2, fir1[maxn], fir2[maxn], rt[maxn], size[maxn];
void addedge(int x, int y, Edge *e, int *fir, int &cnte){Edge &ed=e[++cnte]; ed.fr=x;ed.to=y; ed.nxt=fir[x]; fir[x]=cnte; }int tim, dfn[maxn], low[maxn], w[maxn], st[maxn], tl, n2, isori[maxn];
void tarjan(int u, int p, int &siz, Edge *e, int *fir){ int v;dfn[u]=low[u]=++tim; st[++tl]=u; ++siz;for (int i=fir[u]; i; i=e[i].nxt){if ((v=e[i].to)==p) continue;if (dfn[v]){ low[u]=min(low[u], dfn[v]); continue; }tarjan(v, u, siz, e, fir); low[u]=min(low[u], low[v]); if (low[v]<dfn[u]) continue;int x, cnt=1;while (st[tl+1]!=v){ //�����st[tl]!=u�� x=st[tl--]; ++cnt;addedge(x, n2+1, e2, fir2, cnte2);addedge(n2+1, x, e2, fir2, cnte2); }w[n2+1]=cnt;addedge(n2+1, u, e2, fir2, cnte2);addedge(u, n2+1, e2, fir2, cnte2); ++n2; }
}int siz[maxn];
long long dfs(int u, int p, int n, Edge *e, int *fir){ siz[u]=isori[u]; int v; long long ans=0;for (int i=fir[u]; i; i=e[i].nxt){if ((v=e[i].to)==p) continue;ans+=dfs(v, u, n, e, fir); siz[u]+=siz[v];ans+=1ll*w[u]*siz[v]*(n-siz[v]); //�������������� }ans+=1ll*w[u]*(n-siz[u])*siz[u]; //����Ҳ������ if (isori[u]) ans+=1ll*w[u]*(n-1);return ans;
}int main(){scanf("%d%d", &n, &m); n2=n; int x, y; long long ans=0;for (int i=1; i<=n; ++i) w[i]=-1, isori[i]=1;for (int i=1; i<=m; ++i){scanf("%d%d", &x, &y);addedge(x, y, e1, fir1, cnte1);addedge(y, x, e1, fir1, cnte1); }for (int i=1; i<=n; ++i) if (!dfn[i]) rt[i]=1, tarjan(i, 0, size[i], e1, fir1);for (int i=1; i<=n; ++i) if (rt[i]) ans+=dfs(i, 0, size[i], e2, fir2);printf("%lld\n", ans);return 0;
}