【机器学习】039_合理初始化

本文主要是介绍【机器学习】039_合理初始化，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、稳定训练

目标：使梯度值在更合理的范围内

常见方法如下：

· 将乘法变为加法

        · ResNet：当层数较多时，会加入一些加法进去

        · LSTM：如果时序序列较长时，把一些对时序的乘法做加法

· 归一化

        · 梯度归一化：把梯度转化为一个均值0、方差1这样的数，从而避免梯度的数值过大或过小

        · 梯度裁剪：如果梯度大于一个阈值，就强行拉回来减到一个范围里

· 合理的权重初始化、选取合理的激活函数

二、合理初始化操作

目标：让每层的方差都为一个常数

· 让每层的输出和梯度都看作“随机变量”

· 让输出和梯度的均值和方差都保持一致，那么就可以在每层的传递之间保持，不会出现问题

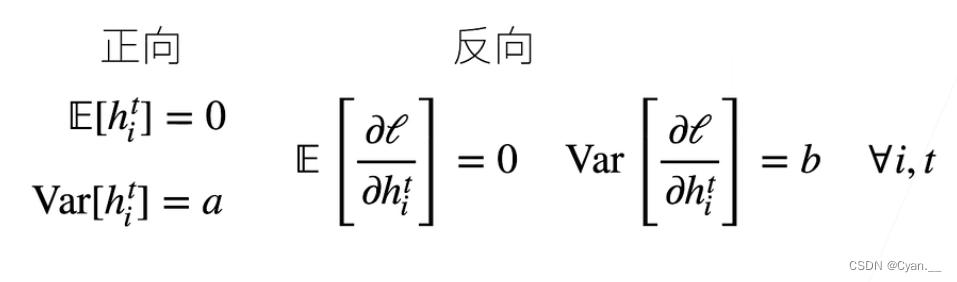
权重初始化

目标：将参数和权重初始化在一个合理的区间值里，防止参数变化过大或过小导致出现问题

· 当训练开始时，数值更易出现不稳定的问题

        · 随机初始的参数可能离最优解很远，更新幅度较陡，损失函数会很大，从而导致梯度较大

        · 最优解附近一般较缓，更新幅度会较小

· 假设不定义初始化方法，框架将使用默认初始化，即采用正态分布初始化权重值

        · 这种初始化方法对小型神经网络较为有效，但当网络较深时，这种初始化方法往往表现较差

· Xavier初始化：

        某些没有非线性的全连接层输出（例如，隐藏变量） 的尺度分布：

        · 对于某一层  输入  以及其相关权重 ，输出由下式给出：

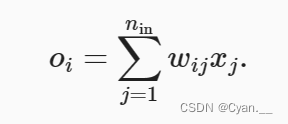
        权重  都是从同一分布中独立抽取的

        · 假设该分布具有均值 0 和方差 （不一定是标准正态分布，只需均值方差存在）

        · 假设层  的输入也具有均值 0 和方差 ，且独立于  并彼此独立

        可以按下列方式计算  的均值与方差：

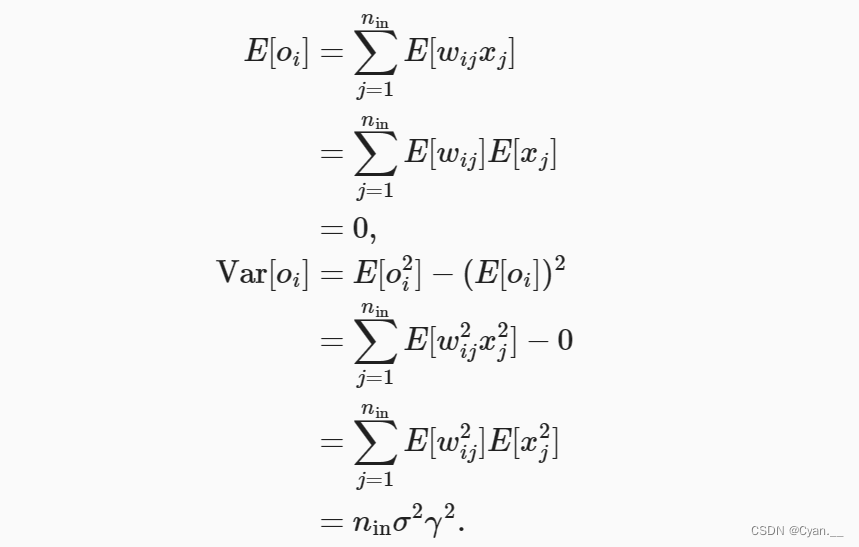
        为了保障  的方差不变化，可设置 。

        现在考虑反向传播过程，我们面临着类似的问题，尽管梯度是从更靠近输出的层传播的。

        使用与前向传播相同的推断，我们可以看到：

        · 除非 ，否则梯度的方差可能会增大。其中  是该层输出的数量。

        · 然而，我们不可能同时满足  和  这两个条件。

        但我们只需满足：

        即可达到要求，这便是Xavier初始化的基础。

        通常，Xavier初始化从均值为 0，方差  的高斯分布中采样权重。

        Xavier初始化表明：

        · 对于每一层，输出的方差不受输入数量的影响；

        · 任何梯度的方差不受输出数量的影响。

这篇关于【机器学习】039_合理初始化的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---