本文主要是介绍第六章 图(下)【图的应用,重难点】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. 最小生成树
1.1 最小生成树的概念
- 生成树:连通图的生成树是包含图中全部顶点的一个极小连通子图。 若图中顶点数为 n,则它的生成树含有 n-1 条边。对生成树而言,若砍去它的一条边,则会变成非连通图,若加上一条边则会形成一个回路。
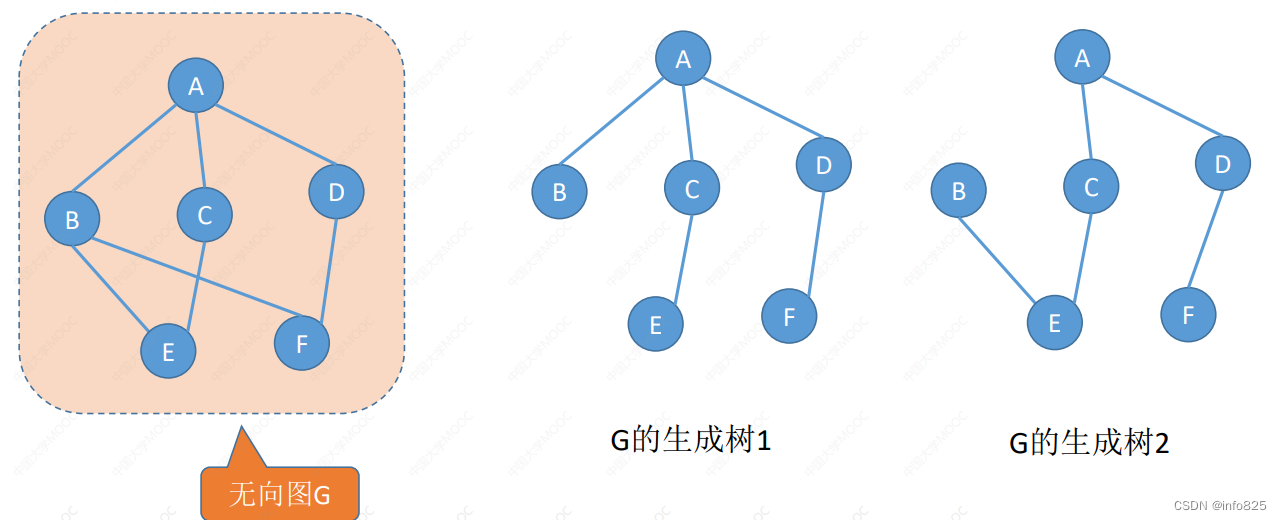
- 最⼩⽣成树(最⼩代价树):对于一个带权连通无向图
,生成树不同,每棵树的权(即树中所有边上的权值之和)也可能不同。设R为G的所有生成树的集合,若T为R中边的权值之和最小的生成树,则T称为G的最小生成树(Minimum-Spannino-Tree,MST).。
- 最小生成树可能有多个,但边的权值之和总是唯一且最小的。
- 最小生成树的边数 =顶点数 -1。砍掉一条则不连通,增加一条边则会出现回路。
- 如果一个连通图本身就是一棵树,则其最小生成树就是它本身。
- 只有连通图才有生成树,非连通图只有生成森林。
求最小生成树的两种方法
1.2 Prim算法(普里姆):
从某一个顶点开始构建生成树;每次将代价最小的新顶点纳入生成树,直到所有顶点都纳入为止。时间复杂度: O(V2)适合用于边稠密图。核心思想:贪心算法
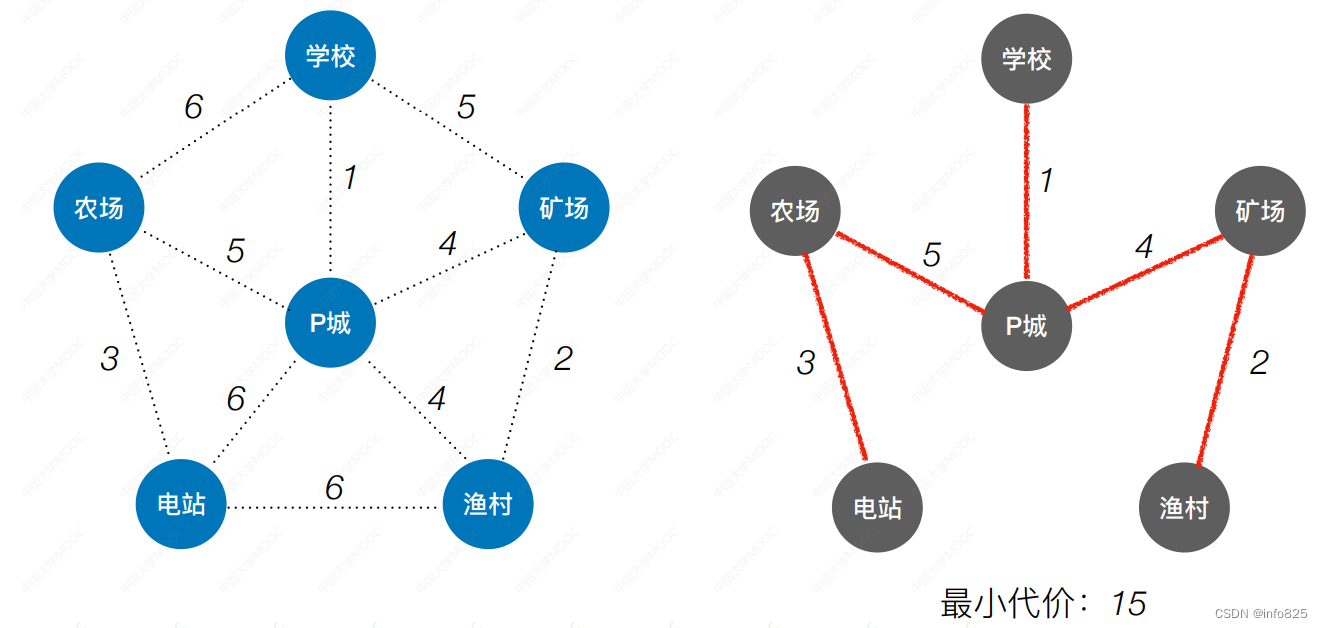
同一顶点开始生成的最小生成树可能也不一样,但是最小代价是一样的
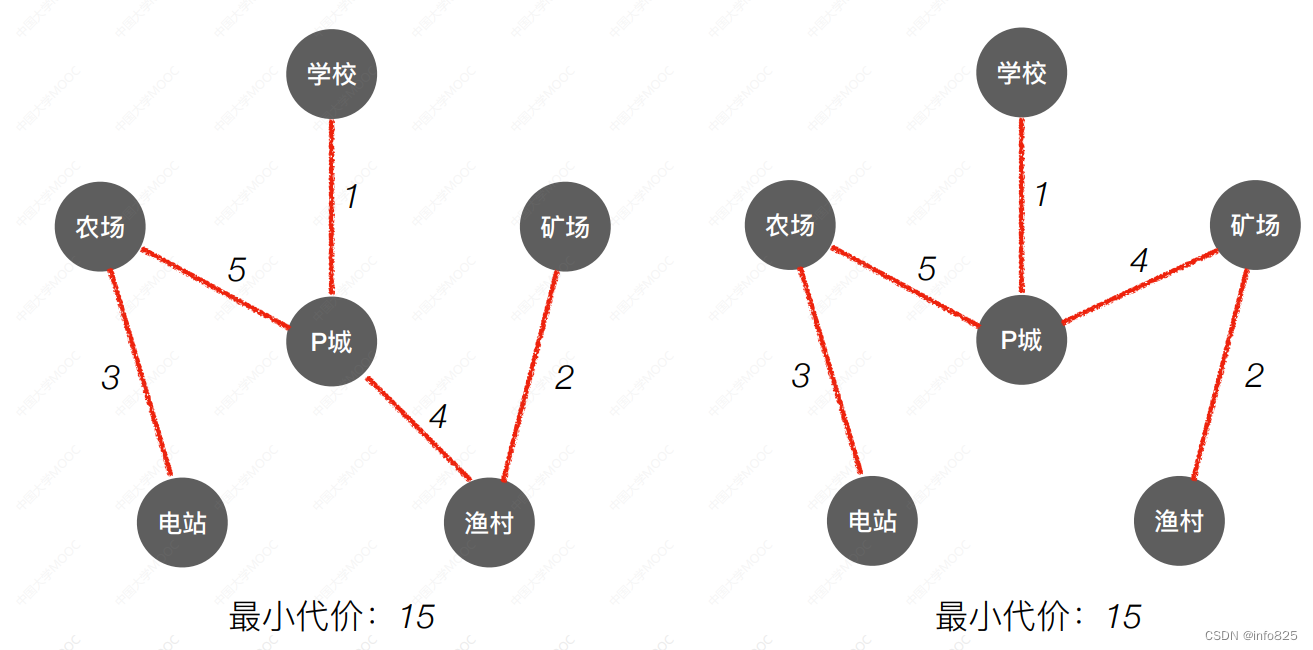
算法实现:
Prim 算法的实现思想:
1.初始:从V0开始,标记各节点是 否已加⼊树isJoin,各节点加⼊树 的最低代价,lowCost
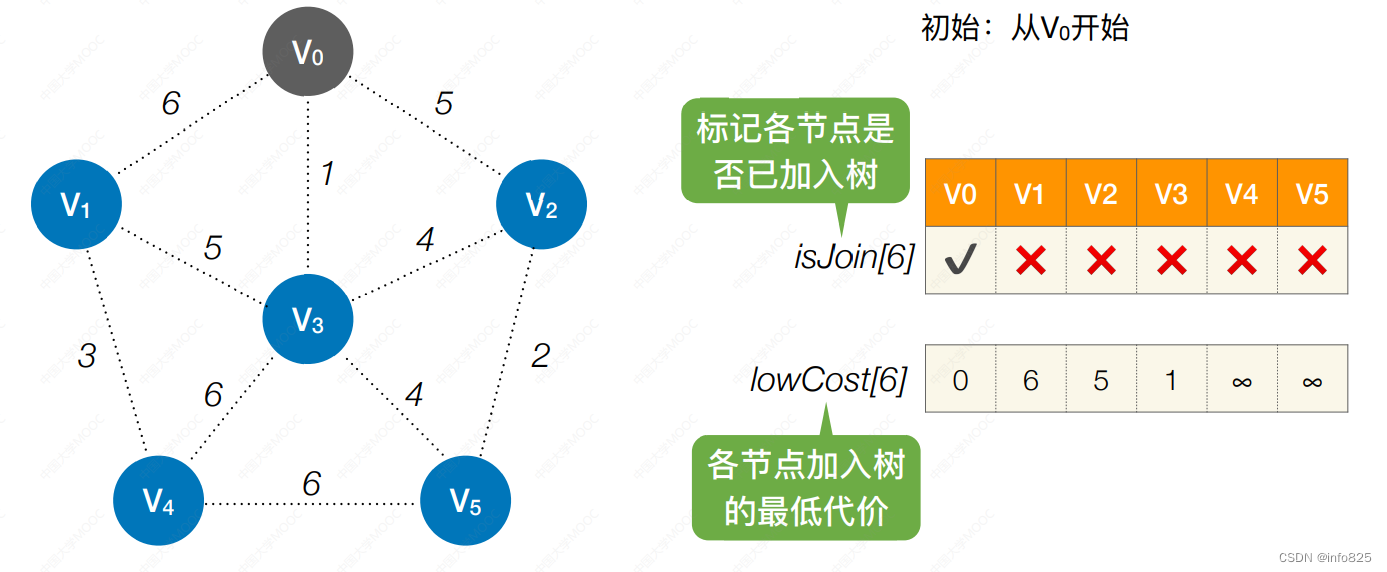
2. 第1轮:循环遍历所有个结点,找 到lowCost最低的,且还没加⼊树 的顶点将该顶点加入树,再次循环遍历,更新还没加⼊的 各个顶点的lowCost值
3. 重复1,2,从V0开始,总共需要 n-1 轮处理,每⼀轮处理:循环遍历所有个结 点,找到lowCost最低的,且还没 加⼊树的顶点。 再次循环遍历,更新还没加⼊的 各个顶点的lowCost值,
每⼀轮时间复 杂度O(2n),总时间复杂度 O(n2),即O(|V|2)
void Prim(G, T)
{// T为空;// U = {w};while((V-U)! = NULL){设(u,v)为让u属于U,v属于(V-U)对最短边T = T U {(u,v)}; //边入树U = U U {v}; //顶点入树}
}//辅助数组:
isJoin[vexNum]; //标记各节点是否已加入树
lowCost[vexNum]; //各节点加入树的最小代价 != 权值,每次并入新节点后都需要更新1.3 Kruskal算法(克鲁斯卡尔):
每次选择一条权值最小的边,使这条边的两头连通(原本已经连通的就不选)直到所有结点都连通。时间复杂度: O(|E|log|E|)适合用于边稀疏图。
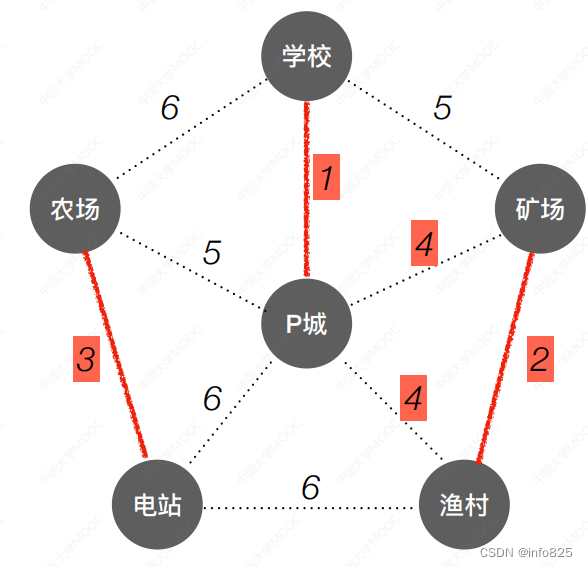
算法实现:
1. 初始:将各条边按权值排序
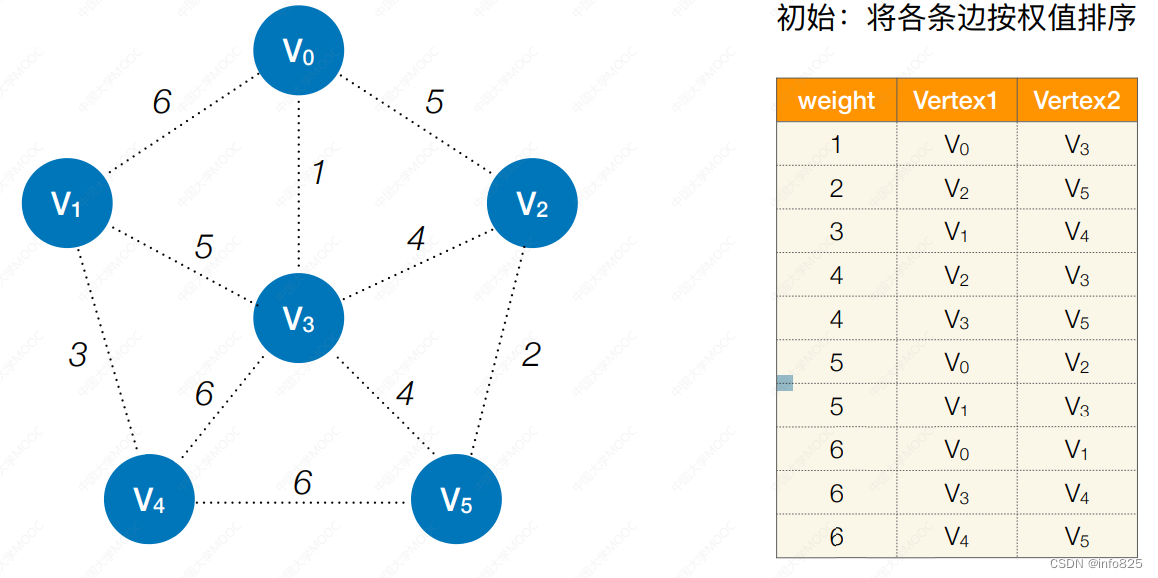
2.第1轮:检查第1条边的两个顶点是否 连通(是否属于同⼀个集合) 不连通,则连起来
2.第i轮:检查第i条边的两个顶点是否 连通(是否属于同⼀个集合)不连通,则连起来,已连通,则跳过
共执⾏ e 轮,每轮判断两个顶点是 否属于同⼀集合,需要 O(log2e) 总时间复杂度 O(elog2e)
void Kruskal(v, T)
{T = v;numS = n; //连通分量数while(numS>1){从E中选取权值最小的边(u,v);if(v和u属于不同连通分量){T = T U {(v,u)}; //边入树numS--;}}
}2. 最短路径问题

2.1 无权图的单源最短路径问题——BFS算法
⽆权图可以视为⼀种特殊的带权图,只是每条边的权值都为1
从2出发寻找无权图的单源最短路径
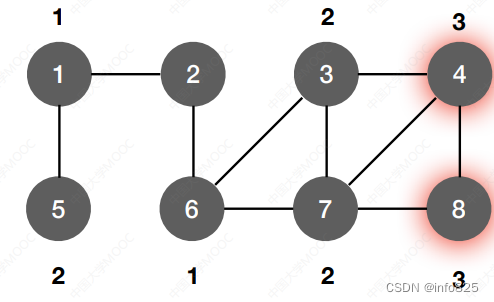
算法实现:
使用 BFS算法求无权图的最短路径问题,需要使用三个数组
d[]数组用于记录顶点 u 到其他顶点的最短路径。path[]数组用于记录最短路径从那个顶点过来。
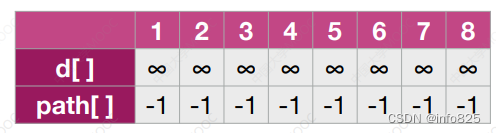
visited[]数组用于记录是否被访问过。

在visit⼀个顶点时,修改其最短路径⻓度 d[ ] 并在 path[ ] 记录前驱结点

代码实现:
#define MAX_LENGTH 2147483647 //地图中最大距离,表示正无穷// 求顶点u到其他顶点的最短路径
void BFS_MIN_Disrance(Graph G,int u){for(i=0; i<G.vexnum; i++){visited[i]=FALSE; //初始化访问标记数组d[i]=MAX_LENGTH; //初始化路径长度path[i]=-1; //初始化最短路径记录}InitQueue(Q); //初始化辅助队列d[u]=0;visites[u]=TRUE;EnQueue(Q,u);while(!isEmpty[Q]){ //BFS算法主过程DeQueue(Q,u); //队头元素出队并赋给ufor(w=FirstNeighbor(G,u);w>=0;w=NextNeighbor(G,u,w)){if(!visited[w]){d[w]=d[u]+1;path[w]=u;visited[w]=TRUE;EnQueue(Q,w); //顶点w入队}}}
}2.2 带权图的单源最短路径问题——Dijkstra算法
相关概念背景
带权路径⻓度——当图是带权图时,⼀条路径上所有边的权值之和,称为该路径的带权路径⻓度
- BFS算法的局限性:BFS算法求单源最短路径只适⽤于⽆权图,或所有边的权值都相同的图。
- Dijkstra算法能够很好的处理带权图的单源最短路径问题,但不适⽤于有负权值的带权图。
算法实现:
使用 Dijkstra算法求最短路径问题,需要使用三个数组:
final[]数组用于标记各顶点是否已找到最短路径。dist[]数组用于记录各顶点到源顶点的最短路径长度。path[]数组用于记录各顶点现在最短路径上的前驱。
1. 初始:从V0开始,初始化三个数组信息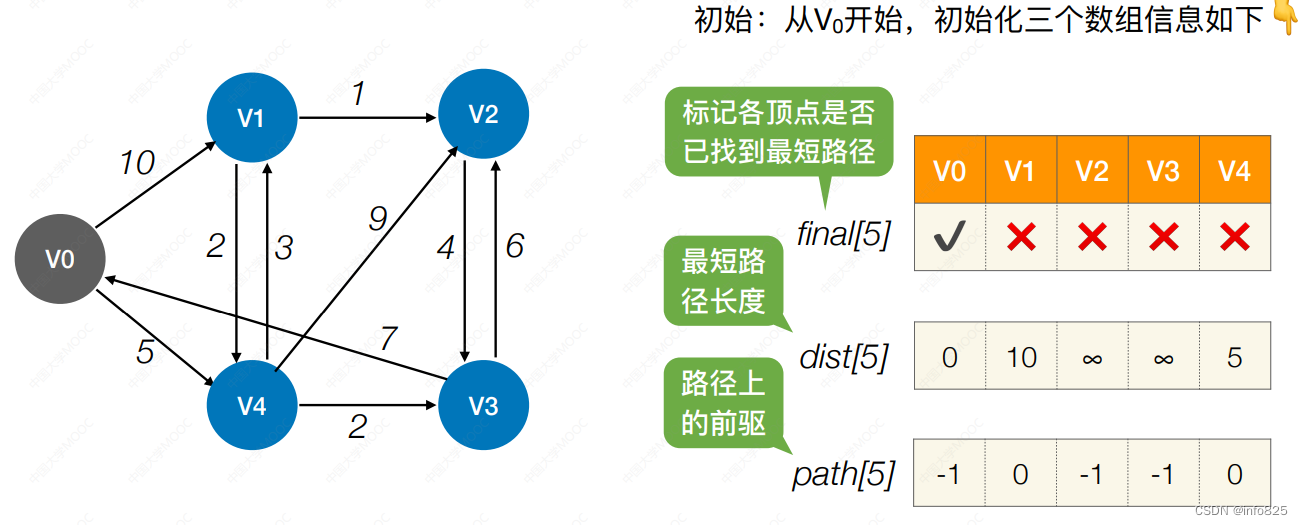
2. 第1轮:循环遍历所有结点,找到还没确定最短 路径,且dist 最⼩的顶点Vi,令final[i]=ture,检查所有邻接⾃ Vi 的顶点,若其 final 值为false, 则更新 dist 和 path 信息
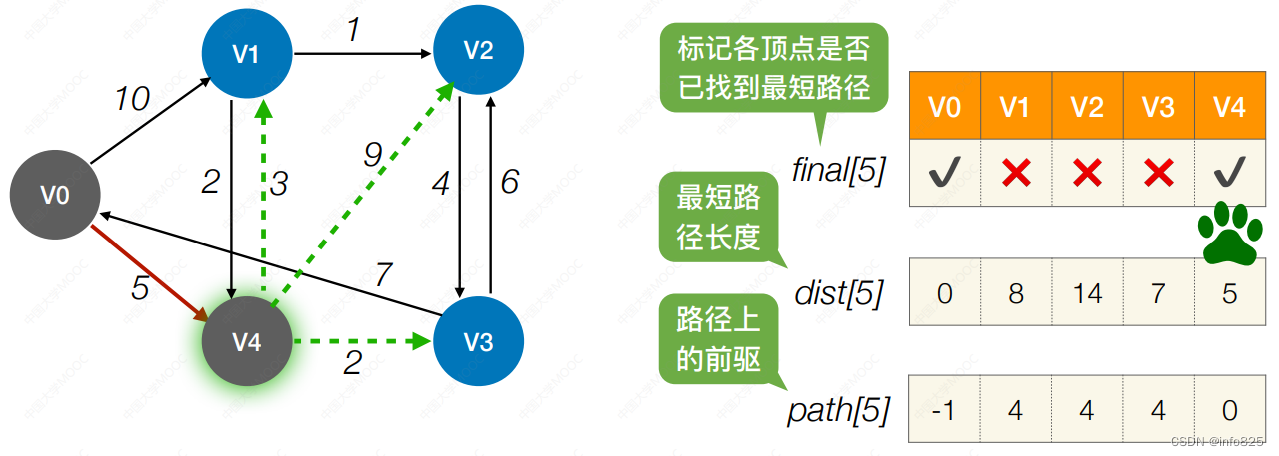
3.重复过程2,n-1轮处理,直到所有顶点的final 值为true.并更新完成
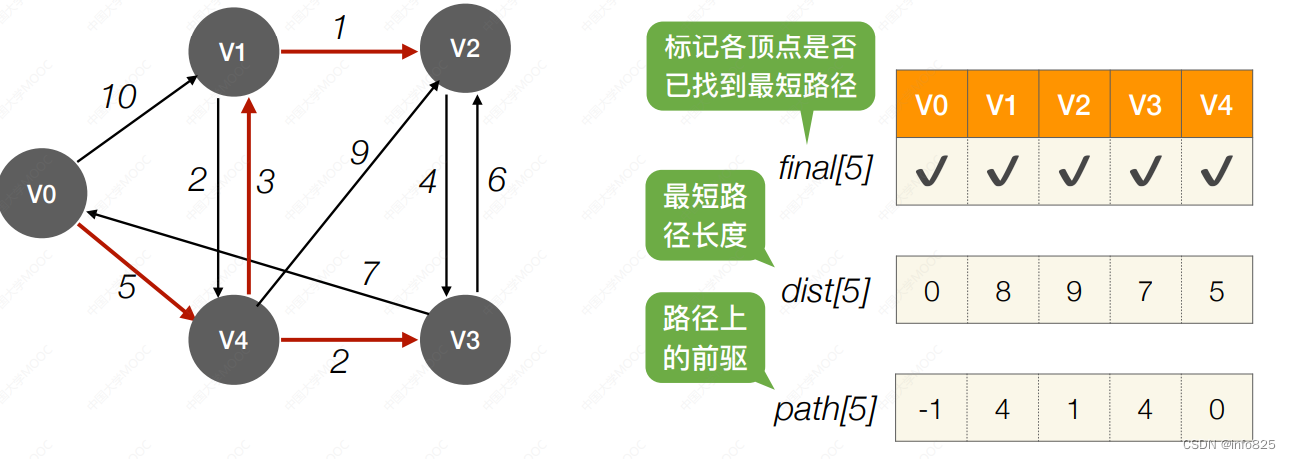
4. 使⽤数组信息

代码实现:
#define MAX_LENGTH = 2147483647;// 求顶点u到其他顶点的最短路径
void BFS_MIN_Disrance(Graph G,int u){for(int i=0; i<G.vexnum; i++){ //初始化数组final[i]=FALSE;dist[i]=G.edge[u][i];if(G.edge[u][i]==MAX_LENGTH || G.edge[u][i] == 0)path[i]=-1;elsepath[i]=u;final[u]=TREE;}for(int i=0; i<G.vexnum; i++){int MIN=MAX_LENGTH;int v;// 循环遍历所有结点,找到还没确定最短路径,且dist最⼩的顶点vfor(int j=0; j<G.vexnum; j++){if(final[j]!=TREE && dist[j]<MIN){MIN = dist[j];v = j;}}final[v]=TREE;// 检查所有邻接⾃v的顶点路径长度是否最短for(int j=0; j<G.vexnum; j++){if(final[j]!=TREE && dist[j]>dist[v]+G.edge[v][j]){dist[j] = dist[v]+G.edge[v][j];path[j] = v;}}}
}时间复杂度: O(n2)即O(|V|2)
2.3 各顶点间的最短路径问题——Floyd算法
2.3.1 Floyd算法基本思想:
求出每⼀对顶点之间的最短路径,使⽤动态规划思想,将问题的求解分为多个阶段。

2.3.2 Floyd算法应用范围
可以⽤于负权值带权图,但是不能解决带有“负权回路”的图(有负权值的边组成回路),这种图有可能没有最短路径。
算法实现:
-
Floyd算法使用到两个矩阵:
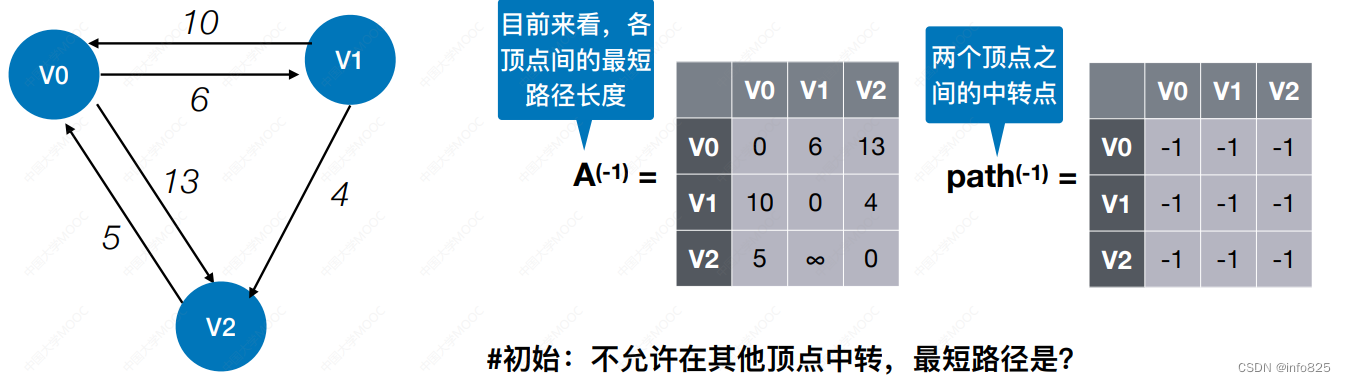
dist[][]:目前各顶点间的最短路径。path[][]:两个顶点之间的中转点。
递推一个n阶方阵序列,
,...,
,...,
,其中
[i][j]表示从顶点vi到vj的长度,k表示绕行第k个顶点的运算步骤,利用
记录节点的中转情况。
步骤:①初始时若v0到vi之间有边,则记录其最短路径为该边权值,若不存在则记∞
②尝试允许经过v0顶点中转,更新顶点间最短路径

③依此尝试允许经过v1,v2,...,vk顶点中转,并不断更新最短路径,,直到允许v(n-1)顶点都经过中转,方阵 [i][j] = Min{[i][j] , [i][k]+[k][j]}
④经过n次迭代,最终[i][j]就是vi到vj的最短路径长度

代码实现:
//初始化矩阵A和path
...
for(int k=0; k<n; k++)
{for(int i=0; i<n; i++){for(int j=0; j<n; j++){if(A[i][j]>A[i][k]+A[k][j]){A[i][j] = A[i][k]+A[k][j]; //更新最短路径长度path[i][j] = k; //中转点}}}
}算法分析:时间复杂度——O(),空间复杂度——O(
)

这篇关于第六章 图(下)【图的应用,重难点】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




