【形式化方法】Part B： LA/LP Applications（子集和问题）

在本节中，我们将研究如何利用LA/LP理论，借助Z3求解器建立模型和解决问题。

具体地说，我们将解决几个非常难的问题，这里的“难”是指这些问题都是np完全的，也就是说，对于这些问题一般没有已知的多项式算法。

但是，您很快就会发现使用LA/LP求解器(如Z3)解决这些问题是多么容易(和多么有趣)。一般来说，您将认识到基于求解器的问题解决策略的威力和简单性。

我们要解决的np完全问题是(其中一些已经在我们之前的讲座中讨论过):

1. 子集和问题
2. N-queen问题
3. 背包问题
4. 线性回归

请注意，这并不是基于SMT的求解器可以处理的问题的完整列表，在您学习了此技术之后，还鼓励您尝试解决其他np完全问题。

子集和问题

子集问题是一个著名的可满足性问题:给定一个多集(一个多集就像一个普通的集合，除了元素可以被重复之外)，我们应该确定一个非空子集T (S)，这样

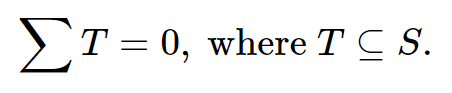 ，在集合中找到子集，使得这个子集的和为0。比如这里有个集合：{-7，-3，-2，7000，5，9}。显然这里有个解：{-3，-2，5}

这个问题是np完全的，关于子集问题的更多背景信息，请参考这篇文章：子集和问题

解释： 我们要找到一个集合中的某个子集相加为0，只需要构造一个X = [x_0,x_1,...x_n]列表。比如在这个集合中{-7，-3，-2，7000，5，9}，对应构造的列表是X  =[x_0,x_1,x_2,x_3,x_4,x_5]

需满足条件①x_0 + x_1 + x_2 + x_3 + x_4 + x_5 ！=0  （因为如果全为0，条件②就永远成立）

                 ②(-7*x_0) + (-3*x_1) + (-2*x_2) + (7000*x_3) + (5*x_4) + (9*x_5) = 0 

能找到满足条件①②的结果就是：x_1 = 0,x_2 = 1,x_3 = 1,x_4 = 1,x_5 = 0,  这样，我们就知道索引为2，3，4对应的值，即[-3, -2, 5] 这个子集之和为0.问题解决。

Exercise 9:阅读subset_sum.py Python文件中的代码，完成subset_sum_la()方法，该方法使用0-1 ILA解决子集和问题。基本思想是为目标集合T中的每个数字创建标志F，我们只需要添加约束：其中N是目标集合S的长度（即实现上述问题的代码）

# LA-based solution
def subset_sum_la(target_set: list):solver = Solver()flags = [Int(f"x_{i}") for i in range(len(target_set))]# 0-1 ILAfor flag in flags:solver.add(Or(flag == 0, flag == 1))# print(flags)# the selected set must be non-emptysolver.add(sum(flags) != 0)# @exercise 9: please fill in the missing code to add# the following constraint into the solver.#       sum_i flags[i]*target_set[i] = 0# raise Todo("exercise 9: please fill in the missing code.")i = 0con = []for t in target_set:con.append(t * flags[i])i = i+1solver.add(sum(con) == 0)# print(con)if __name__ == '__main__':# a small test casesmall_set = [-7, -3, -2, 9000, 5, 8]print(subset_sum_la(small_set))

输出结果：  可满足，并且找到子集 [-3, -2, 5]

Exercise 10：subset_sum.py Python文件中的代码，subset_sum_dp()方法已经提供了基于动态编程(DP)的解决方案。并给出了另一种基于拉普拉斯算子的subset_sum_la_opt()方法，该方法利用Z3伪布尔约束条件进行优化。试着比较DP、LA算法和优化的LA算法的效率，通过将max_nums的值更改为其他值，例如200,2000,20000，…你的观察结果是什么?从这些数据中你能得出什么结论?

# LA 优化算法
def subset_sum_la_opt(target_set: list):solver = Solver()# enable Pseudo-Boolean solver# to get more information about Pseudo-Boolean constraints# refer to https://theory.stanford.edu/~nikolaj/programmingz3.htmlsolver.set("sat.pb.solver", "solver")# use Pseudo-Boolean constraints for each flagflags = [Bool(f"x_{i}") for i in range(len(target_set))]#solver.add(AtLeast(flags + [1]))# the selected set must be non-emptysolver.add(PbGe([(flags[i], 1) for i in range(len(target_set))], 1))# selected set must sum to zerosolver.add(PbEq([(flags[i], target_set[i]) for i in range(len(target_set))], 0))start = time.time()result = solver.check()print(f"time used in LA optimized: {(time.time() - start):.6f}s")if result == sat:return True, [target_set[index] for index, flag in enumerate(flags) if solver.model()[flag]]return False, result

# DP算法
def subset_sum_dp(target_set):def subset_sum_dp_do(the_set, target, index):if index == 0:return Falseif target == the_set[index - 1]:return Trueif subset_sum_dp_do(the_set, target, index - 1):return Truereturn subset_sum_dp_do(the_set, target - the_set[index - 1], index - 1)start = time.time()result = subset_sum_dp_do(target_set, 0, len(target_set))print(f"time used in DP: {(time.time() - start):.6f}s")return result

def gen_large_test(n):nums = [10000] * nnums[len(nums) - 2] = 1nums[len(nums) - 1] = -1# print(nums)return numsif __name__ == '__main__':# a large test casemax_nums = 20large_set = gen_large_test(max_nums)"""# @exercise 10: compare the efficiency of the DP and theLP algorithm, by changing the value of "max_nums" to othervalues, say, 200, 2000, 20000, 200000, ...what's your observation? What conclusion you can draw from these data?raise Todo("exercise 10: please fill in the missing code.")""""""max_num = 20time used in LA: 0.070020stime used in LA optimized: 0.020002stime used in DP: 0.667767sLA优化算法比LA算法速度快，DP算法速度最慢，到max_num = 200时，DP算法用时更长了。"""print(subset_sum_la(large_set))print(subset_sum_la_opt(large_set))print(subset_sum_dp(large_set))

运行结果：
结论：max_num = 20
time used in LA: 0.070020s
time used in LA optimized: 0.020002s
time used in DP: 0.667767s
LA优化算法比LA算法速度快，DP算法速度最慢，到max_num = 200时，DP算法用时更长了（没有运行下去）。

#中科大软院-hbj形式化课程笔记-欢迎留言与私信交流

#随手点赞，我会更开心~~^_^