【位操作】大吉大利

https://ac.nowcoder.com/acm/contest/4853/A

比赛思路：

感觉没有思路，感觉挺无奈的，没有发现其中的奥秘。

确实是一道想通了就不难的题目。比赛的时候应该把所有的二进制显示都列出来看一下的，说不定能发现规律。

只会暴力的思路：

for(int i=0;i<n;i++){for(int j=0;j<n;j++){ans+=(a[i]&a[j]);}
}

但是一看数据范围就知道这样肯定是行不通的，至少也要O（nlogn）的算法~哎

题解：

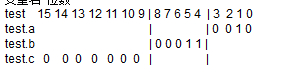
光想是想不出来，不如列出来看一下？

比如说有5个数字，只看他们的末位：

1

0

1

0

1

并运算的规则是：有0出0，全1出1，所以一定要一对里两个同时为1才行。

按照题目的规则，则

则可以知道该位 1 的个数的平方，也就是该列两两互相&再相加的结果

每次列都这么操作，同时因为要将二进制转换为十进制，所有每次算出来的值还要乘上2的次方，

就像这里因为是最后一位，所以是  *  。

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
int n,a[100005];
ll ans,cnt,nw;int read(){int x=0;char ch=getchar();while(!isdigit(ch)) ch=getchar();while(isdigit(ch)) x=(x<<3)+(x<<1)+(ch^48),ch=getchar();return x;
}int main(){n=read();for(int i=1;i<=n;i++) a[i]=read();for(int i=27;i>=0;i--){cnt=0,nw=1ll<<i;//当前位为1，后面的位都为0；for(int j=1;j<=n;j++) if((a[j]&nw)) cnt++;//数这一位有几个1ans+=nw*cnt*cnt;}printf("%lld\n",ans);return 0;
}

这样的速度是很快的，

这里再放上另一种,方便理解

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a[100005], ans=0;ll pow(int base, int n){//快速幂ll sum=1;while (n){if (n&1) sum = base*sum;base *= base;n >>= 1;}return sum;
}int main(){ll n, maxc=0; scanf("%lld", &n);for (int i=1; i<=n; i++){ll num, cnt=0, nm; scanf("%lld", &num);while (num){if (num&1) a[cnt] ++;cnt++;num >>= 1;}maxc = max(maxc, cnt);}for (int i=0; i<maxc; i++) ans += a[i]*a[i]*pow(2, i);printf("%lld", ans);
}​