从DES走到AES（现代密码的传奇之路）

本文主要是介绍从DES走到AES（现代密码的传奇之路），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言铺垫：

DES：

密钥如何生成：

密码分组；

伽罗瓦域：

AES：

接下来我们进入算法核心——“轮函数”：

接下来，密钥的生成：

结语：

前言铺垫：

计算机中，所有的信息数据都用二进制来保存

XOR（异或）是天然的加密算法：我们假设明文A经过密钥（XOR运算）B得到密文C。且我们只能看到密文C。当密文C为1时，你分不清是A是1还是B是1。反之，当密文C为0时，你分不清AB是全为0还是全为1。所以很明显，异或运算有着50%的随机，完美的随机。

受限于软硬件的处理性能，计算机处理数据时将大数据分块，分成一个个64bit的数据块，对每一块进行XOR加密，再重组，这样，加密所需要点密钥的长度就和分组的长度一样（64bit）。可惜的是这样依然可以通过频率破解来破译出明文，所以我们还需要另一种牢靠的算法让密文的数字更难以预料。搞信息论的香农在这篇开启了现代密码学大门的论文里《Communication Theory of Secrecy Systems*》将这样模糊密钥和密文关系的加密算法称之为：”混淆（confusion）“混淆很常见于古典密码（单表替换，维吉尼亚，Enigma），但这种混淆之后的关系还是有迹可循，而0和1却为混淆带来了更多的可能性

我们以加密100101为例：

看起来毫无规律，但还不够，对于分段存储于硬盘不同区域的信息，如果两个明文差异微小，在密文上的反应，也只是区域里有限位数的不同，这些差异就是破译者的福音。想要消解规律也很简单，打乱顺序就可以了。但这并没有解决明文自身的统计特性，所以，我们要让一个明文的变化影响多个密文，也就是“扩散（diffusion）”

输入里有一半的数据被置换了两次，这样以来，修改输入中的一个数字，就有50%可能改变输出中的两个数字

如果说混淆掩盖了密钥的踪迹，那扩散就是进一步扰乱明文的规律。

XOR，扩散，混淆，于是在1977年，一种以此为基础的加密算法横空出世——DES（Data Encryption Standard）。

这是DES的原理图

DES：

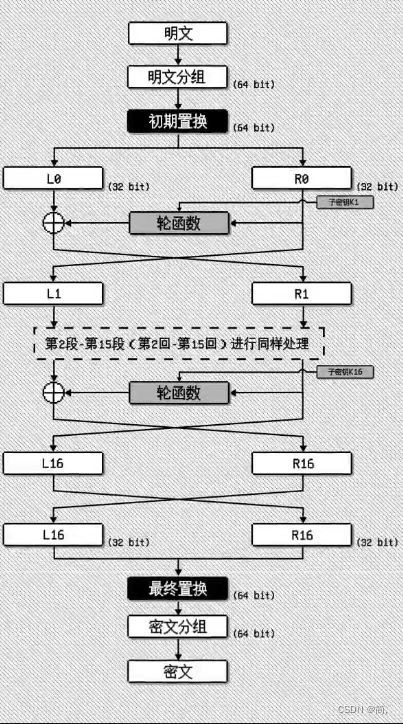
其中算法最核心的部分“轮函数”就是你所熟知的扩散加混淆。

我们把一个32bit的明文扩散成48bit，我们称这个扩散的表盒为“E盒”。

接下来，密钥进场，与之异或，异或后的结果被分为8组，一组6bit，每组数据分别游经自己的“S盒”形成8个4bit的结果，最终进行合并，正好又恢复了32bit。还没完，我们将结果再进行一次扩散，这次的表盒称之为“P盒”，注意此次扩散后依然为32bit，此时的结果就是最终的结果。

以上就是DES大名鼎鼎的“轮函数”，但轮函数只加密了一半的明文，因为一开始就被分为两组，各32bit，R0经过了复杂的轮函数之后在与L0进行异或，生成R1，L1什么也不用做，直接由R0得来（未加密前），再将L1和R1交换位置，两者拼接，就是密文，这就是著名的“Feistel加密结构”

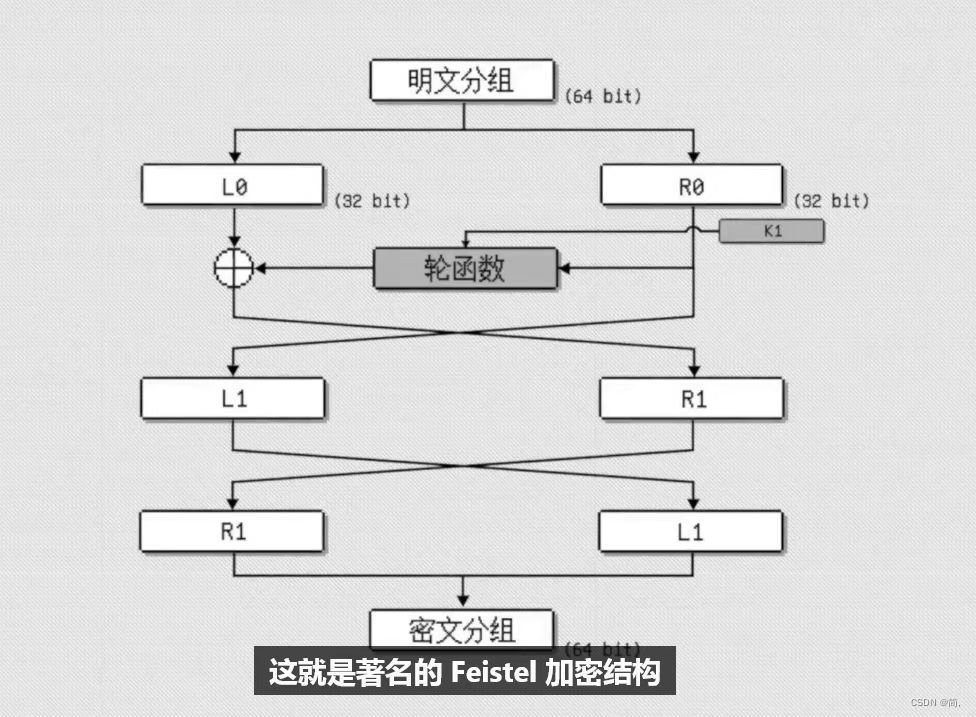
为什么要分成两组？为什么L1不需要计算直接继承R0？为什么最后还要进行交换？

一切的一切都是为了——解密，解密就是将密文再加密一遍，其核心就是异或

那么这样的一次加密安全吗？对于心思缜密的密码学家来说，肯定不够！DES采用了16轮加密，每一轮都让密码的复杂度指数级上涨，每一轮都在放大明文和密文的差异。最后的最后，就是开头和结尾增加一次移位，也称为置换，这就是全部的“DES”

现在的密码大多都超出了普通人理解的极限，DES只是一个开始，却让我们思考如何让它呈现的时候，费劲了心力！

密钥如何生成：

还是为了安全性，16轮加密用了16个不同的密钥。你首次手动输入的密钥应该为64bit，它首先被置换为56bit（选择置换），消失的8位不参与加密，用于进行“奇偶校验”（不做展开），然后将56bit的数据分为两组，分别进行一次“左巡回转换”——数据左移1位，接着两组数据合并再进行一次置换为48bit（压缩置换），为第一轮的子密钥。

接下来，用合并前的C1和D1再进行一次左巡回转换（不同轮数，坐循环的次数也不同）得到C2和D2，进行一次置换得到第二轮的子密钥。如此往复，我们就得到了16个不同的子密钥。

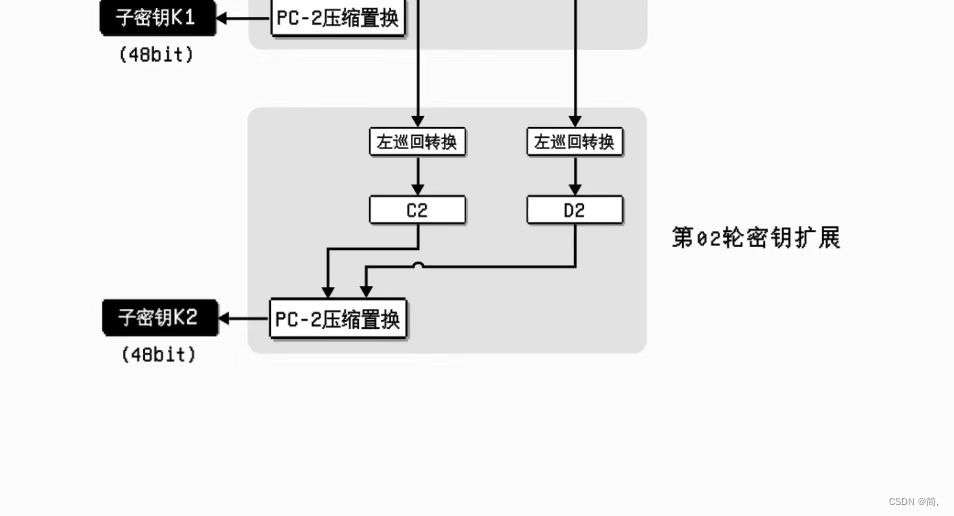
附上一张大局图：

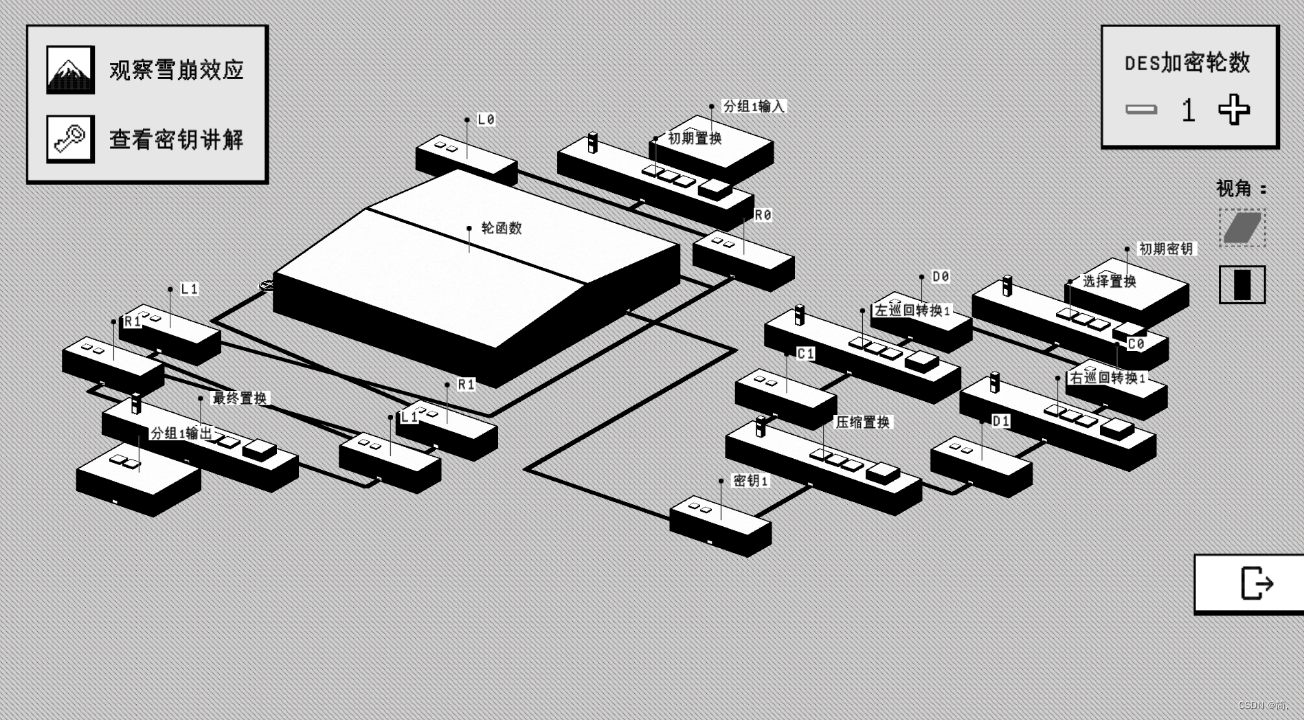
DES自诞生之初就饱受争议，它不安全吗？恰恰相反，只要密钥够长，它就足够安全。它为人诟病的是人们不知道它为什么安全。于此同时，密钥的 $2^{64}$ 种可能性都抵御不了迅猛发展的计算机技术，1999年DES被暴力破解，耗时22小时15分钟，这也标志着密码学正式推出了密码学历史的舞台

密码分组；

注意了，DES只能处理64bit的数据，但现在的数据动不动就上万bit，怎么解决呢？——密码分组，把数据拆分成n个64bit的数据块，分别进行DES然后再进行重组，听上去很合理，但是——怎么组？最暴力的方法就是直接拼接，这种简单粗暴的模式就是——ECB（电子密码本模式）：直接将加密完成后的数据拼起来，明文块与密文块一一对应。现在互联网时代海量的数据重复，这就是ECB的漏洞。所以很清晰，DES让单组数据变得安全，却还需要分组模式为整条明文保驾护航。

这里不再过多展开，附上几种常见的分组模式的解析图（初始化向量为计算机随机生成）

ECB（电子密码本模式）：

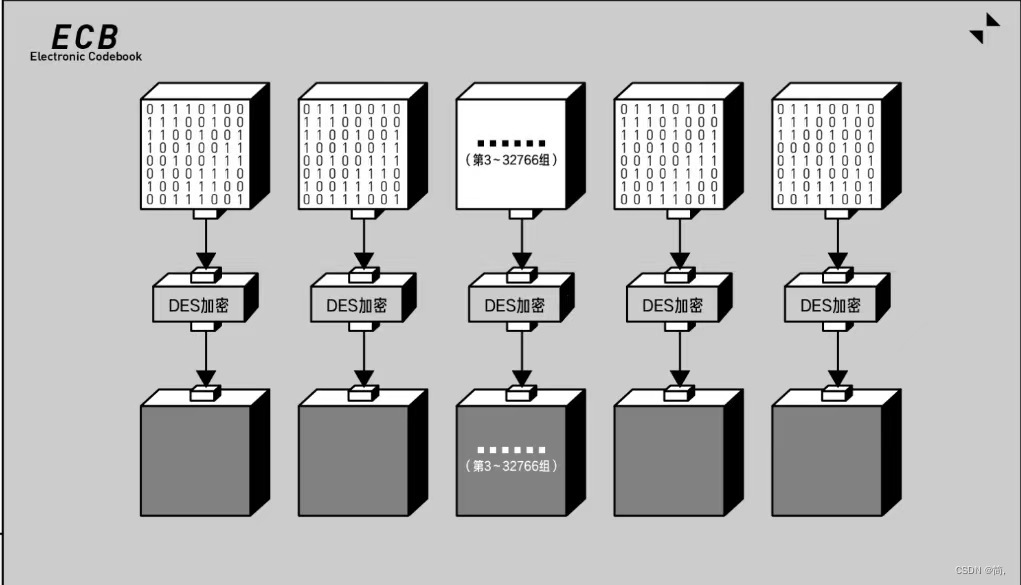
CBC（密码分组链条模式）：

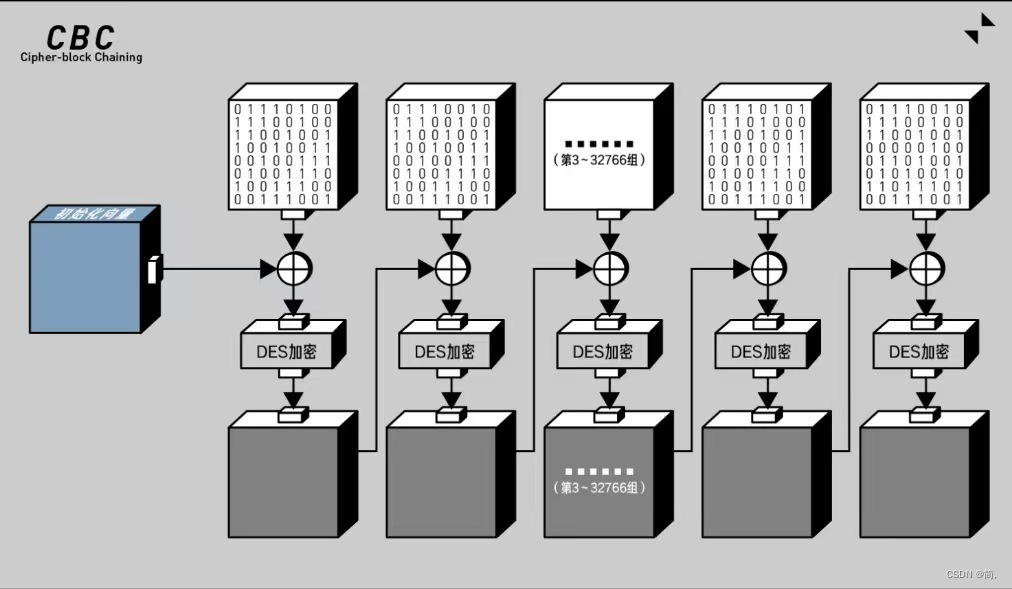
CFB（密文反馈模式）：

OFB（输出反馈模式）：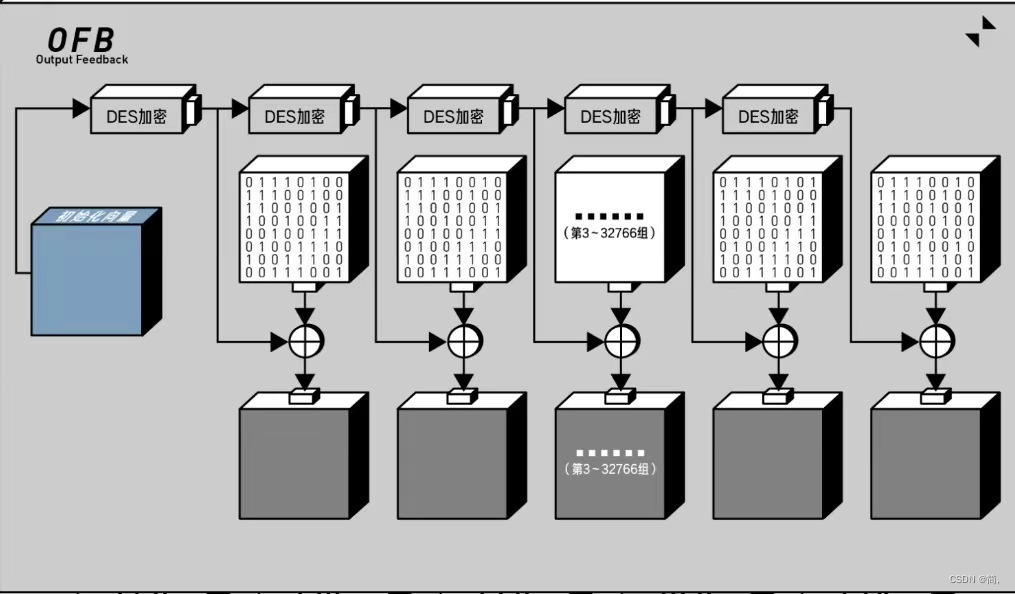

CTR（计算器模式）：

伽罗瓦域：

有限域亦称伽罗瓦域（galois field），是仅含有限个元素的域。用GF(pⁿ)表示pⁿ元的有限域.GF(pⁿ)的乘法群是(pⁿ-1)阶的循环群。p为一个素数，n是一个正整数，F中元素的个数为pⁿ

在抽象代数中，域是一种可进行加、减、乘和除运算的代数结构。域是环的一种。域和一般环的区别在于域要求它的元素可以进行除法运算，这等价于每个非零的元素都要有乘法逆元。同时，在现代定义中，域中元素关于乘法是可交换的。简单来说，域是乘法可交换的除环。乘法非交换的除环则称为体，或者反称域。

如果域F只包含有限个元素，则称其为有限域。有限域中元素的个数称为有限域的阶。尽管存在有无限个元素的无限域，但只有有限域在密码编码学中得到了广泛的应用。每个有限域的阶必为素数的幂，即有限域的阶可表示为pⁿ（p是素数、n是正整数），该有限域通常称为Galois域(Galois Fields)，记为GF(pⁿ)。

当n=1时，存在有限域GF（p），也称为素数域。在密码学中，最常用的域是阶为p的素数域GF（p）或阶为 $2^{m}$ 的GF( $2^{m}$ )域

域中减法：找加法逆元（加负数，相加等于0），本质是加法

域中除法：找乘法逆元（乘倒数，相乘等于1），本质是乘法，没有乘法逆元说明不能做除法

正式定义：

数字世界不在无穷无尽，而是有限闭合，这就是有限域（只有有限个数，运算结果仍是它们本身，这是没有进位的计算）

ps：进位是最影响计算机效率的东西

GF(2)有限域：

异或就是GF（2）里的加法运算，减法和加法没有区别

乘法是与（AND）运算

其他非有限域全部可以构成以阶为 $2^{m}$ 的GF( $2^{m}$ )域

如GF（8）是非有限域，因为不是所有的数都有乘法逆元，那如果是GF（ $2^{3}$ ）呢？答案就留给你自己来验证吧！

一路来我们学习了DES，密码分组模式和伽罗瓦域，这样以来，我们终于获得了一张前往罗马的机票。等等，为什么是罗马？

AES：

1999年，DES被暴力破解出来的明文信息“See you in Rome"，是来自罗马的邀请函。1999年3月22日一场影响深远的算法评审会在罗马召开，来自全球的密码学专家齐聚一堂，商讨DES的继任者

2001年11月26日，美国国家标准组织宣布来自比利时的Rijndeal算法摘得这一桂冠，成为新的高级加密标准，也就是大名鼎鼎的AES（Advanced Encryption Standard）

现在是2022年，但这个算法还没有过时，仍然统治着你我所熟知的数字世界，无法撼动。

接下来，进入正题：

AES同DES一样，数据太长，加密前需要进行分组。不同的是，AES把分组长度提升到128bit，然后再细分为16个小组，每组8bit，排进状态矩阵。

先来看看AES的三种规格：

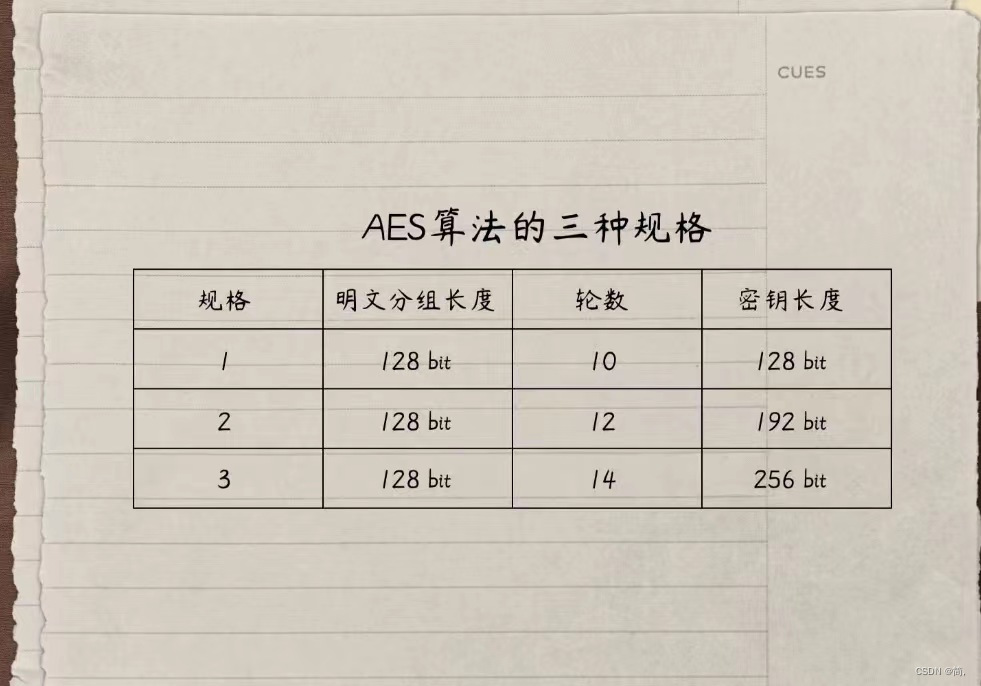
用同一个轮函数迭代加密是分组密码的常见操作

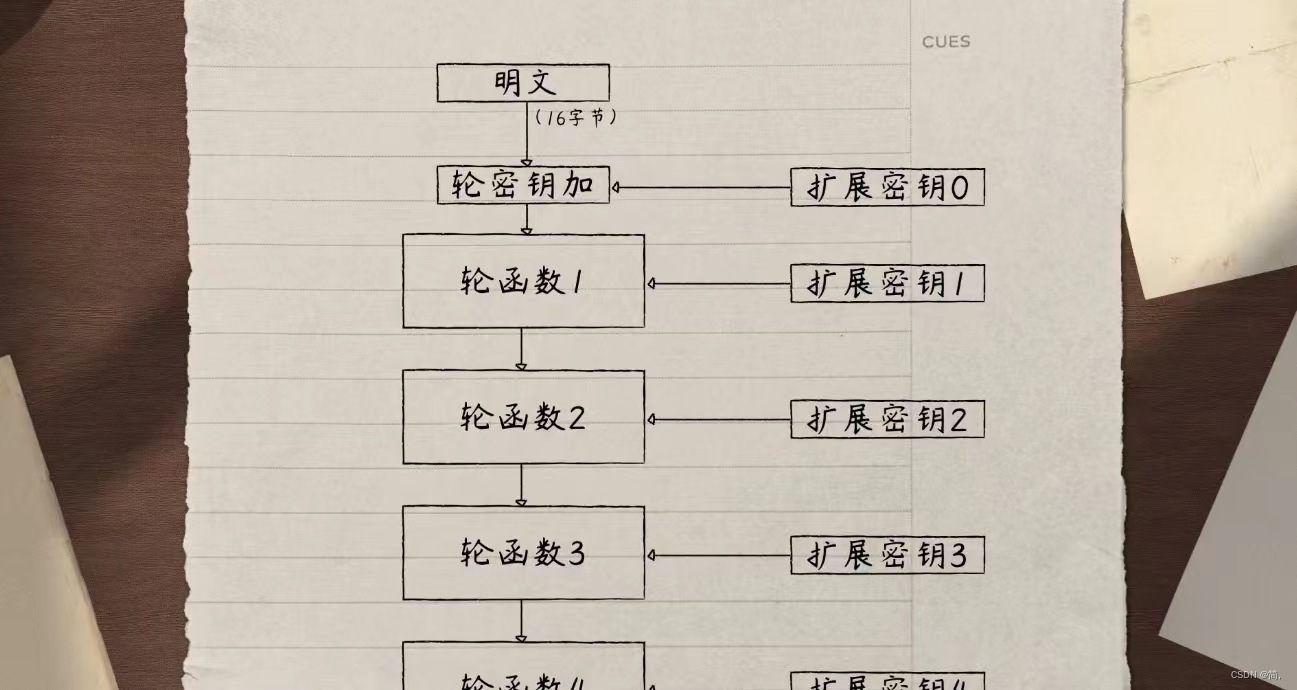
进入加密前，会让子密钥和明文进行一次异或，我们称之为——“轮密钥加”

接下来我们进入算法核心——“轮函数”：

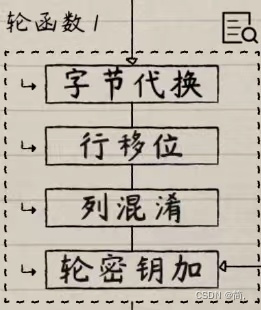
轮函数主要包含 4 种运算，但不同的运算轮所做的具体运的算组合并不相同。主要区别是初始轮（Round 0）和最后一轮（Round Nr），所有中间轮的运算都是相同的，会依次进行 4 种运算，即：

[数据混淆] 字节代换（SubByte）
[数据混淆] 行移位（ShiftRow）
[数据混淆] 列混合（MixColumn）
[数据加密] 轮密钥加（AddRoundKey）

第一步——“字节代换”：不同于DES人为的构造S盒，人们把目光投向数学。仔细观察状态矩阵里每个小组都是8bit，也就是256种可能性，所以很自然，人们想到了由256组成的GF（ $2^{8}$ ）

AES直接把这个域里数字的逆元设为密文

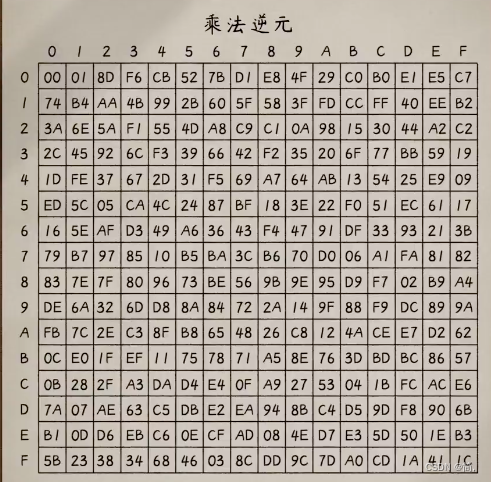
下次加密时直接查表就可以了。

但是，这样可以吗？仔细观察00没有乘法逆元，01的乘法逆元可以它本身。明文和密文一样很危险，所以还需要一步仿射变换。步骤如下

看不懂没有关系，举个例子就好了：

第二步也可以简化为这样：

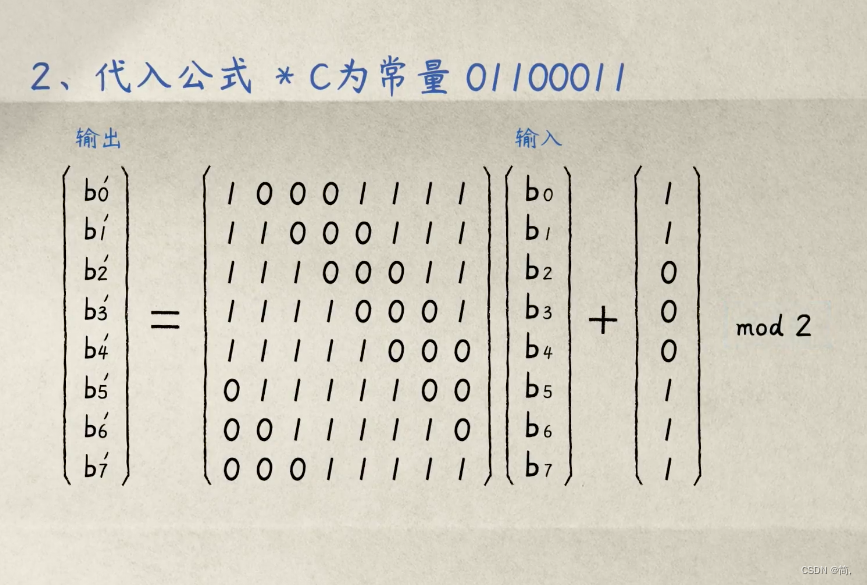
可以看到矩阵中，每行每列都有5个1，改变一位输入，输出就会完全不同，这样数据十分的随机

最终我们得到了这样的一张表，还是什么也不用干，得到输入后查表就可以了：

这张表的本质就是“混淆”，因此也可以被称为——“S盒”

第二步是——“行移位”：

这步很简单，把第二行往左移1位，第三行2位，第四行3位，除了第一行，其他三行的位置都发生了变化，也就是——行的“扩散”

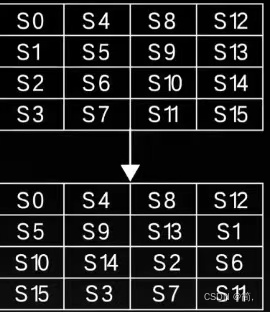
第三步——“列混淆”：

这步更加简单明了，将状态矩阵和一个常数矩阵相乘以达成列上的“扩散”

例如：

每列的输出都被相同列所有的输入影响，同时每一列的输入，都由上一步行的元素决定，两者的叠加让每个输出数据被所有的输入数据影响，这是极其有效的扩散

最后一步——“轮密钥加”：

这一步和最开始的“轮密钥加”是相同的，和子密钥进行一次异或运算，十分简单

至此，一轮轮函数结束

通常最后一轮的轮函数是没有“列混淆”的，只进行三步。

接下来，密钥的生成：

AES随机生成初始密钥是128位，同样分成16个字节，排列成状态矩阵，然后用于第一次“轮密钥加”。为了增加密钥随机性，还要进行密钥拓展，生成轮函数加密所需的子密钥。

首先让每列的四个数据一组，用W0，W1，W2，W3表示，被叫做——“字”，子密钥按照下图公式生成：

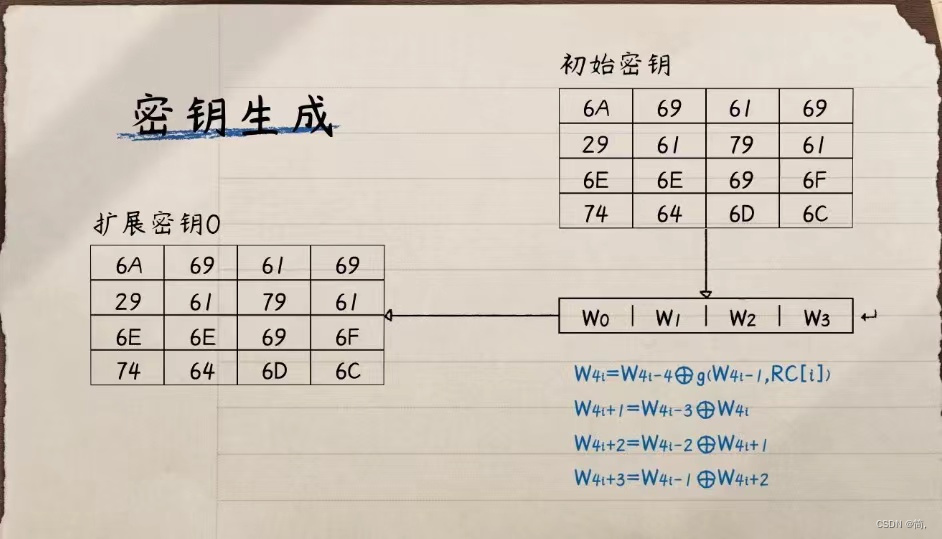
让i = 1就能算出W4到W7，以此类推，如此：

下一轮的子密钥都是由上一轮的子密钥得来，如拉链一样，环环相扣

最后来看g函数：

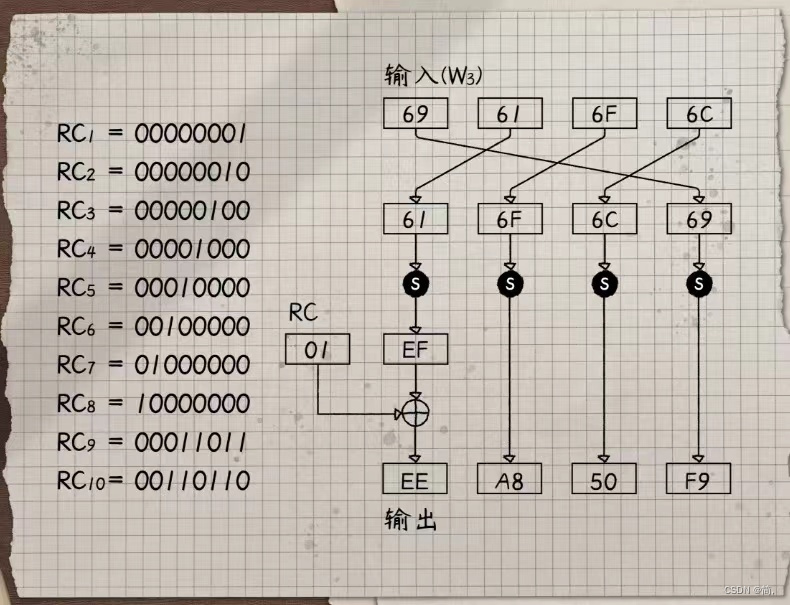
分成三步：

先是简单的扩散，再经S盒处理，最后与一个名为RC的常数进行异或，每轮RC的值都不一样。

我们继续来看AES的解密：

轮函数的每一步均可逆，所以解密就是加密的逆过程

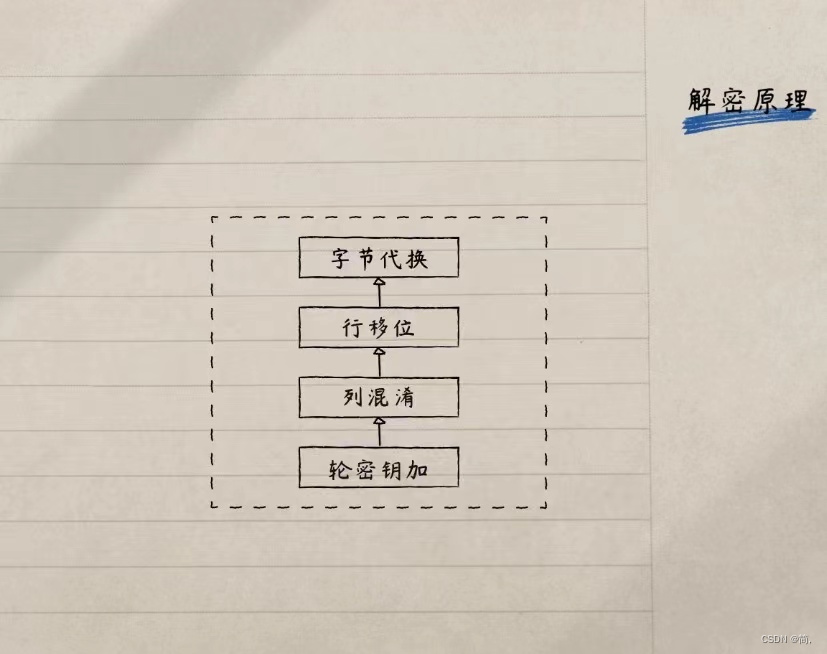
先由密文和最后一轮的子密钥进行异或，接着就是行移位——左移变成右移，最后是逆向字节代换，仍然是查表即可：

这样一轮轮过后，最后一次“轮密钥加”就是最初的明文！

额外说一下，我们日常生活中如WX使用的加密算法就是AES，但是如何进行安全的传输密钥呢？这就要用到非对称加密了。用公钥加密AES的密钥，接收方再用私钥解开，形成安全的通信（双方共同使用相同的AES密钥），因为加解密对称密码比加解密非对称密码的效率高的高的多！如下

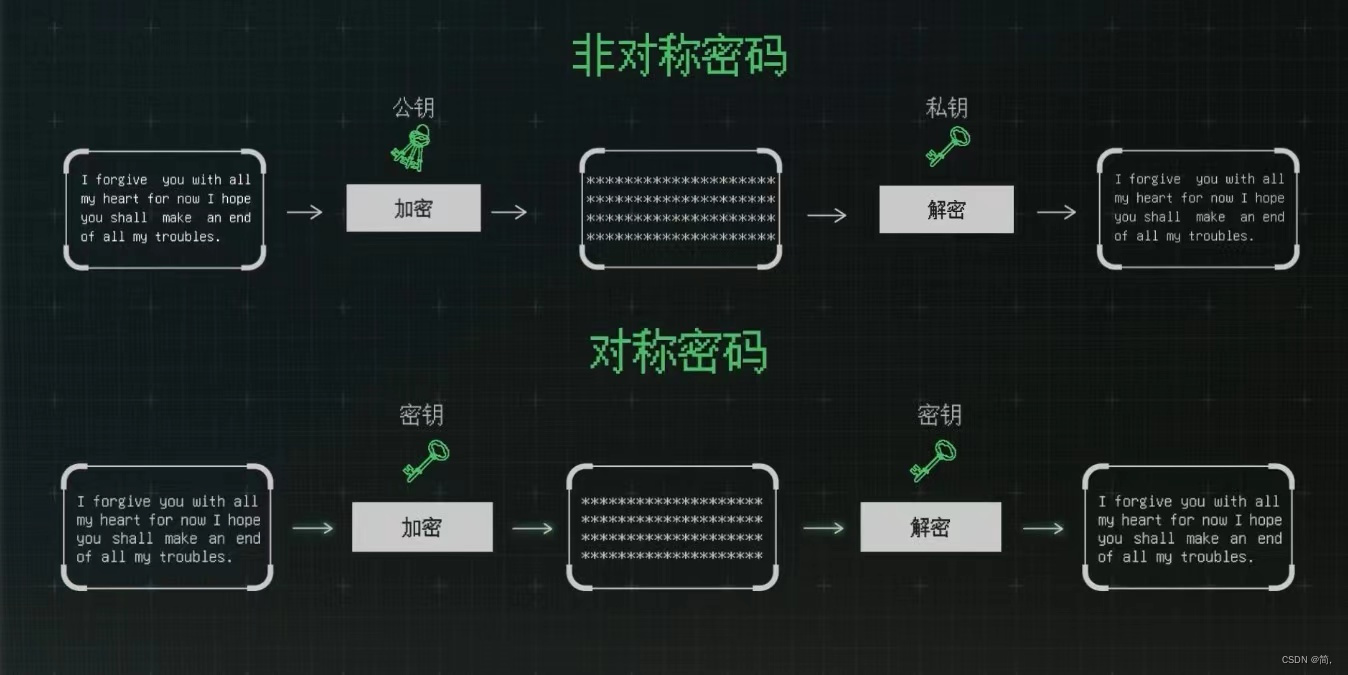
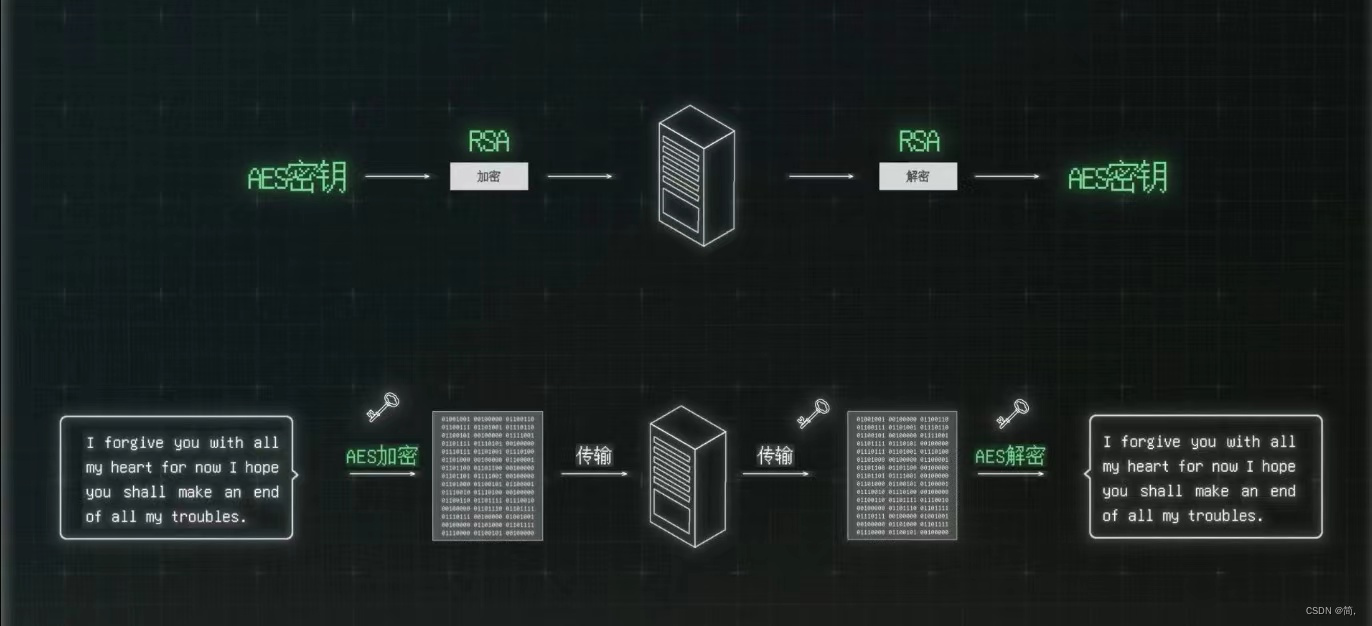
至此——完结撒花：

这就是你一路走来寻找的密码算法，一切都是可以落于纸笔的算法，这些复杂，抽象的符号，无一不表示了当然生活的复杂性。只是这样的复杂被封装了起来。我们不需要学会如果去使用，因为它在无声无息的在网络的世界中为你保驾护航，而且，这是到目前为止，尚未出现有效破译方法到密码算法。这就是它的本质——“复杂，无聊“所以——你需要它吗？你没有需要保护的商业机密也没有需要传递的秘密情报。将一串串明文变成这种极其复杂的密文，有何意义？

而这，正是你需要继续去探索的东西。