MATLAB计算光的折射（二）

计算不同角度的能流反射率和能流透射率、相位变化。

从光疏到光密：

clear;
close all;n1 = 1;   %空气折射率
n2 = 1.45;%平板玻璃折射率
theta = 0:0.1:90;%角度从0到90
a = theta*pi/180;%角度转化为弧度
rp = (n2*cos(a)-n1*sqrt(1-(n1/n2)^2*(sin(a)).^2))./(n2*cos(a)+n1*sqrt(1-(n1/n2)^2*(sin(a)).^2));
tp = (2*n1*cos(a))./(n2*cos(a)+n1*sqrt(1-(n1/n2)^2*(sin(a)).^2));
rs = (n1*cos(a)-n2*sqrt(1-(n1/n2)^2*(sin(a)).^2))./(n1*cos(a)+n2*sqrt(1-(n1/n2)^2*(sin(a)).^2));
ts = (2*n1*cos(a))./(n1*cos(a)+n2*sqrt(1-(n1/n2)^2*(sin(a)).^2));Rp = abs(rp).^2;
Rs = abs(rs).^2;
Rn = (Rp+Rs)/2;Tp = n2*sqrt(1-(n1/n2)^2*(sin(a)).^2)./(n1*cos(a)).*abs(tp).^2;
Ts = n2*sqrt(1-(n1/n2)^2*(sin(a)).^2)./(n1*cos(a)).*abs(ts).^2;
Tn = (Tp+Ts)/2;subplot(1,2,1);
plot(theta,Rp,'-',theta,Rs,'-.',theta,Rn,'--','linewidth',2);
legend('R_p','R_s','R_n');
xlabel('\theta_i');
ylabel('Amplitude');
title(['n_1=',num2str(n1),',n_2=',num2str(n2)]);
axis([0 90 0 1]);
grid on;subplot(1,2,2);
plot(theta,Tp,'-',theta,Ts,'-.',theta,Tn,'--','linewidth',2);
legend('T_p','T_s','T_n');
xlabel('\theta_i');
ylabel('Amplitude');
title(['n_1=',num2str(n1),',n_2=',num2str(n2)]);
axis([0 90 0 1]);
grid on;

结果:

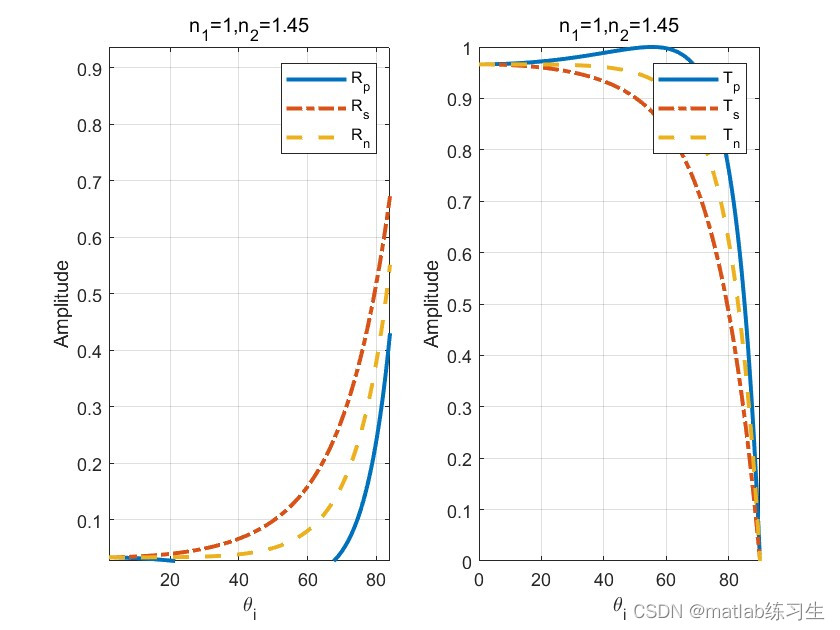
可以看出：
1、当入射角等于0时，能流反射率和能流透射率都不为0；
2、当入射角等于90时，能流反射率为1，能流透射率为0；
3、存在一个特殊角度（布鲁斯特角），使得Rp（p偏振的能流反射率为0），Tp等于1；
4、随着角度不断增大，Rn不断增大，Tn不断减少，但两者的和始终为1；

反过来从光密到光疏也是这样计算：

%从光密到光疏clear;
close all;n1 = 1.45;   %空气折射率
n2 = 1;%平板玻璃折射率
theta = 0:0.1:90;%角度从0到90
a = theta*pi/180;%角度转化为弧度
rp = (n2*cos(a)-n1*sqrt(1-(n1/n2)^2*(sin(a)).^2))./(n2*cos(a)+n1*sqrt(1-(n1/n2)^2*(sin(a)).^2));
tp = (2*n1*cos(a))./(n2*cos(a)+n1*sqrt(1-(n1/n2)^2*(sin(a)).^2));
rs = (n1*cos(a)-n2*sqrt(1-(n1/n2)^2*(sin(a)).^2))./(n1*cos(a)+n2*sqrt(1-(n1/n2)^2*(sin(a)).^2));
ts = (2*n1*cos(a))./(n1*cos(a)+n2*sqrt(1-(n1/n2)^2*(sin(a)).^2));Rp = abs(rp).^2;
Rs = abs(rs).^2;
Rn = (Rp+Rs)/2;Tp = n2*sqrt(1-(n1/n2)^2*(sin(a)).^2)./(n1*cos(a)).*abs(tp).^2;
Ts = n2*sqrt(1-(n1/n2)^2*(sin(a)).^2)./(n1*cos(a)).*abs(ts).^2;
Tn = (Tp+Ts)/2;subplot(1,2,1);
plot(theta,Rp,'-',theta,Rs,'-.',theta,Rn,'--','linewidth',2);
legend('R_p','R_s','R_n');
xlabel('\theta_i');
ylabel('Amplitude');
title(['n_1=',num2str(n1),',n_2=',num2str(n2)]);
axis([0 90 0 1]);
grid on;subplot(1,2,2);
plot(theta,Tp,'-',theta,Ts,'-.',theta,Tn,'--','linewidth',2);
legend('T_p','T_s','T_n');
xlabel('\theta_i');
ylabel('Amplitude');
title(['n_1=',num2str(n1),',n_2=',num2str(n2)]);
axis([0 90 0 1]);
grid on;

结果：

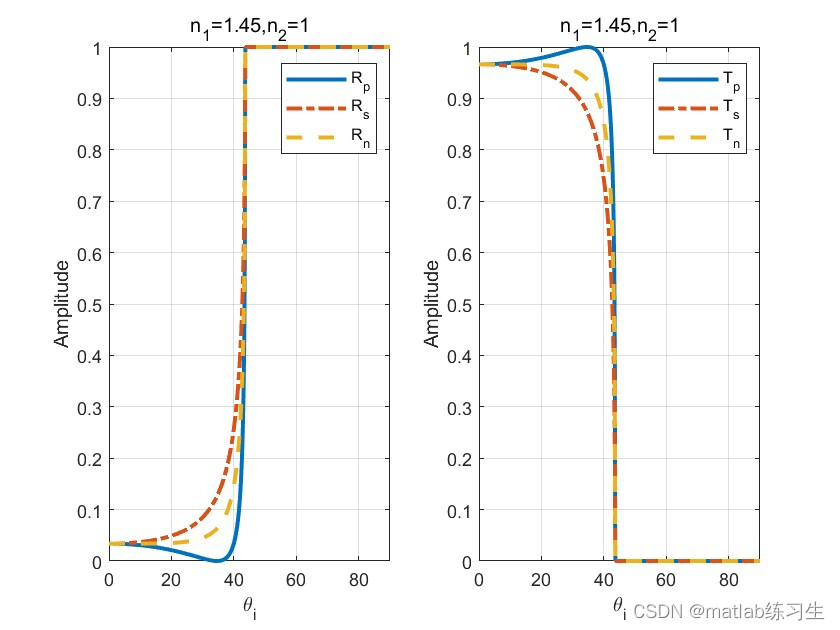
可以看出，此时的布鲁斯特角比较明显，且超过全反射角后，反射能流密度为1，投射能流密度为0；

为了进一步了解在全反射中的物理规律，我们绘制反射和投射率的相位变化图形：

clear;
close all;n2 = 1;   %空气折射率
n1 = 1.45;%平板玻璃折射率
theta = 0:0.1:90;%角度从0到90
a = theta*pi/180;%角度转化为弧度
rp = (n2*cos(a)-n1*sqrt(1-(n1/n2)^2*(sin(a)).^2))./(n2*cos(a)+n1*sqrt(1-(n1/n2)^2*(sin(a)).^2));
tp = (2*n1*cos(a))./(n2*cos(a)+n1*sqrt(1-(n1/n2)^2*(sin(a)).^2));
rs = (n1*cos(a)-n2*sqrt(1-(n1/n2)^2*(sin(a)).^2))./(n1*cos(a)+n2*sqrt(1-(n1/n2)^2*(sin(a)).^2));
ts = (2*n1*cos(a))./(n1*cos(a)+n2*sqrt(1-(n1/n2)^2*(sin(a)).^2));arp=angle(rp);
ars=angle(rs);
atp=angle(tp);
ats=angle(ts);figure(1);
subplot(1,2,1);
plot(theta,arp,'-',theta,ars,'--','linewidth',2);
legend('arg(r_p)','arg(r_s)');
xlabel('\theta_i');
ylabel('\phi');
title(['n_1=',num2str(n1),',n_2=',num2str(n2)]);
axis([0 90 -3.5 3.5]);
grid on;subplot(1,2,2);
plot(theta,atp,'-',theta,ats,'--','linewidth',2);
legend('arg(t_p)','arg(t_s)');
xlabel('\theta_i');
ylabel('\phi');
title(['n_1=',num2str(n1),',n_2=',num2str(n2)]);
axis([0 90 -3.5 3.5]);
grid on;

结果：

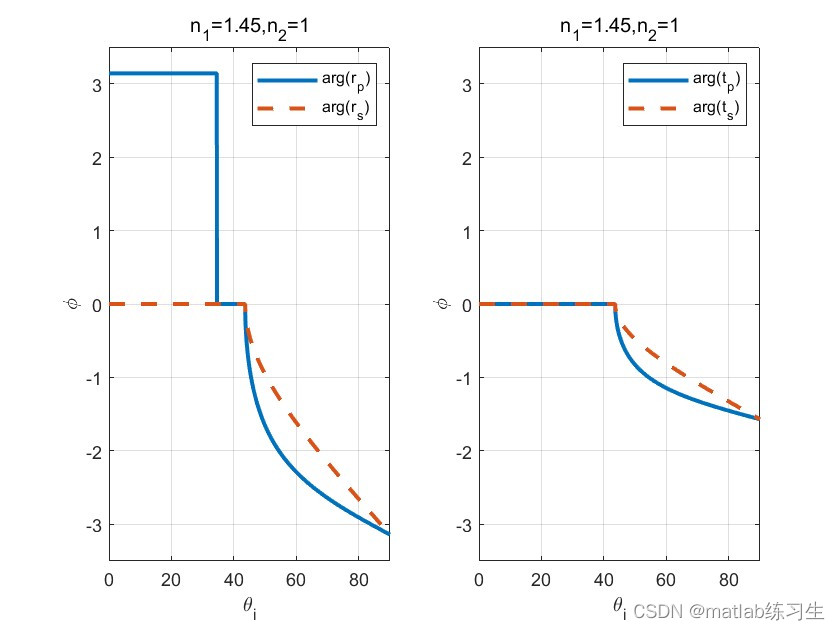
其实从之前振幅透射率的变化图可以看出（大于0时相位相同，小于0时相差π相位）
但是这里需要注意的是，当入射角大于全反射角后，相位没有立刻突变，而是按照一定的趋势逐渐趋于某个值。
tp、ts逐渐趋近于-π/2
rp、rs逐渐趋近于-π
其他的变化率在小于全反射角是相位变化都为0，但是rp的相位相差π
半波损失：波从波疏介质射向波密介质时反射过程中，反射波在离开反射点时的振动方向相对于入射波到达入射点时的振动相反，或者说，反射波相对于入射波相位突变π，这种现象叫做半波损失
倏逝波：沿着z轴方向（入射面和界面的交线方向）传播，在x方向（垂直界线向光密介质内运动的方向）指数衰减的波。
穿透深度很小，仅有波长量级。
可能在z轴方向发生古斯汉欣位移，也是在波长量级。要求入射光束宽度很小。

来源《高等光学仿真——光波导、激光》