本文主要是介绍李航机器学习 | (6) 统计学习方法(第2版)笔记 --- 朴素贝叶斯法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1. 导读
2. 朴素贝叶斯法的学习与分类
3. 朴素贝叶斯法的参数估计
4. 朴素贝叶斯法的参数估计推导
5. 小结
1. 导读
朴素贝叶斯(naive Bayes)法是基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的训练集,首先基于特征条件独立假设学习输入输出的联合概率分布;然后基于此模型,对给定的输入x,利用贝叶斯定理求出后验概率最大的输出y。
统计学习方法的第一章曾对统计学习方法进行了分类,根据模型形式的不同,可以分为决策函数和条件概率分布。在决策函数中,给定一个输入X,通过一个决策函数f,得到预测值Y,即Y=f(X)。在条件概率分布中,给定一个输入X,得到输出Y的条件概率分布P(Y|X),通过这个分布对Y进行决策,如果Y是分类变量,那么就选取概率最大时对应的分类。
统计学习方法可以分为生成模型和判别模型:
1)生成模型:
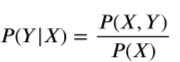
2)判别模型(有两种形式):
![]()
上述三个分类模型的比较:
1)Y=f(X)决策函数形式,它不考虑X和Y的随机性;Y的条件概率分布P(Y|X),只考虑了Y的随机性,给定X时,Y有一个概率分布;第三种形式,同时考虑了X,Y的随机性,不仅有Y的条件概率分布,也有X的边际分布以及X和Y的联合分布。所以从左到右,考虑的随机性是越来越多的。
2)之前第二章中我们学习的感知机模型属于决策函数形式。我们现在学习的朴素贝叶斯法,该模型直接从第一种形式到第三种形式,里面用到了重要的贝叶斯公式。
2. 朴素贝叶斯法的学习与分类
- 基本表示
设输入空间是n维向量的集合,输出空间为类别标记集合
.输入实例特征向量
,输出类别标记
.
X是定义在输入空间上的随机向量(每个特征/分量是一个随机变量),Y是定义在输出空间Y上的随机变量。P(X,Y)是X和Y的联合(概率)分布。
训练集:由联合分布P(X,Y)独立同分布产生。
- 训练:
朴素贝叶斯法通过训练数据集学习联合概率分布P(X,Y).具体的学习以下先验概率分布和条件概率分布。
先验概率分布:.
条件概率分布:
从而学习到联合概率分布P(X,Y).
但是条件概率分布有指数级数量的参数(需要计算的概率是指数级的),我们设特征
有
个取值,j=1,...,n,Y的取值有K个,那么参数有
个,其估计实际上是不可行的。
条件独立性假设:
朴素贝叶斯法对条件概率分布作了条件独立性假设。因为这是一个较强的假设,所以朴素之名由此而来。具体地,条件独立性假设(简化)是:
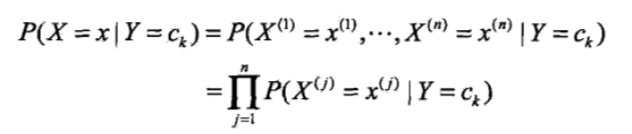
朴素贝叶斯法实际上学到生成数据的机制,属于生成模型。条件独立性假设等于用于分类的特征在类确定的条件下都是条件独立的。这一假设使朴素贝叶斯法变得简单,参数量减少,但有时会牺牲一定的分类准确率。
- 预测
在进行分类时,对于给定的输入x,通过学习到的模型(先验概率分布,条件概率分布)计算后验概率分布,把后验概率最大的类作为x的类别输出。后验概率根据贝叶斯定理计算:

带入条件独立性假设:
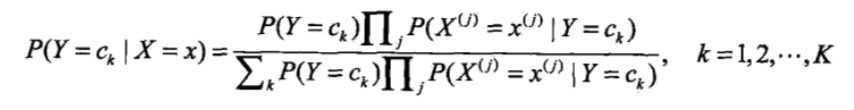
所以朴素贝叶斯分类器可以表示为(找到一个类别ck使得上式/后验概率最大):
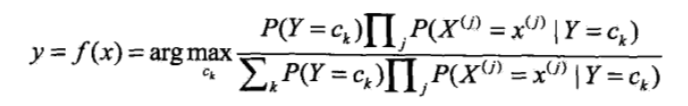
注意到,上式分母对于所有的都是一样的(与类别
无关,相当于一个归一化因子,求整体的最大值等价于求分子的最大值),所以:

- 小结
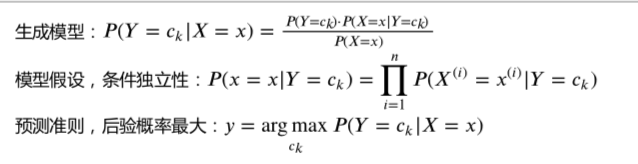
- 后验概率最大化的含义
朴素贝叶斯法将实例分到后验概率最大的类中。这就等价于期望风险最小化。
证明:

3. 朴素贝叶斯法的参数估计
在朴素贝叶斯法中,学习意味着估计,
.有极大似然估计和贝叶斯估计两种方法。
- 极大似然估计
先验概率的极大似然估计为:
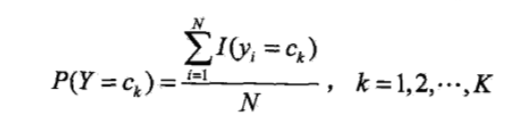
也就是训练数据集中类别为的样本数除以总样本数。
设第j个特征可能的取值集合为{
},条件概率
的极大似然估计为:
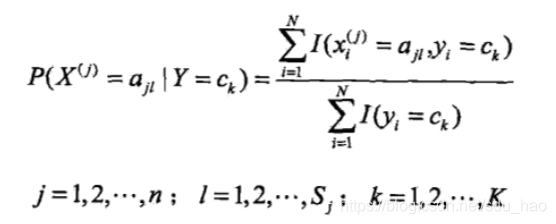
也就是训练数据集中类别为的样本的第j个特征取值为
的样本数除以类别为
的样本数。其中
表示第i个样本的第j个特征,
表示第j个特征的第l个可能取值。
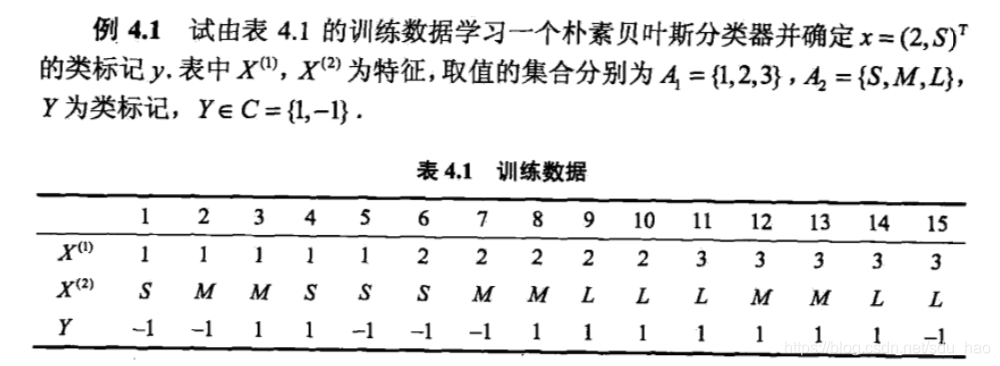
例题:

- 贝叶斯估计
极大似然估计可能会出现要估计的概率值(参数)为0的情况,比如当训练样本比较少时,可能某些类的样本不存在,即,条件概率的极大似然估计中分母此时会出现为0的情况。这会影响到后验概率的计算结果,使得分类产生偏差。
可以使用贝叶斯估计解决这一问题。也就是进行平滑操作,可以把他的思想理解为“劫富济贫”,不会出现0概率的情况,对于数据集中没有出现的情况也会分配一个小概率,相应地对大概率(出现次数比较多)进行一定的削弱,以保证概率和为1.
条件概率的贝叶斯估计为:
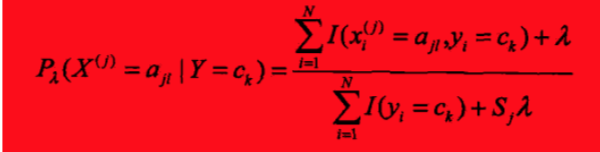
其中.等价于在随机变量各个取值的频数上赋予一个正数
.
时就是极大似然估计。通常取
,称为拉普拉斯平滑。
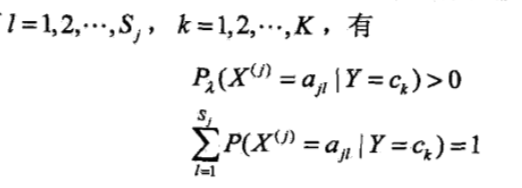
说明上式是一个概率分布。
先验概率的贝叶斯估计为:
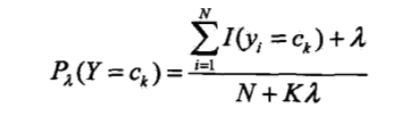
例题:

按照拉普拉斯平滑计算概率,即.
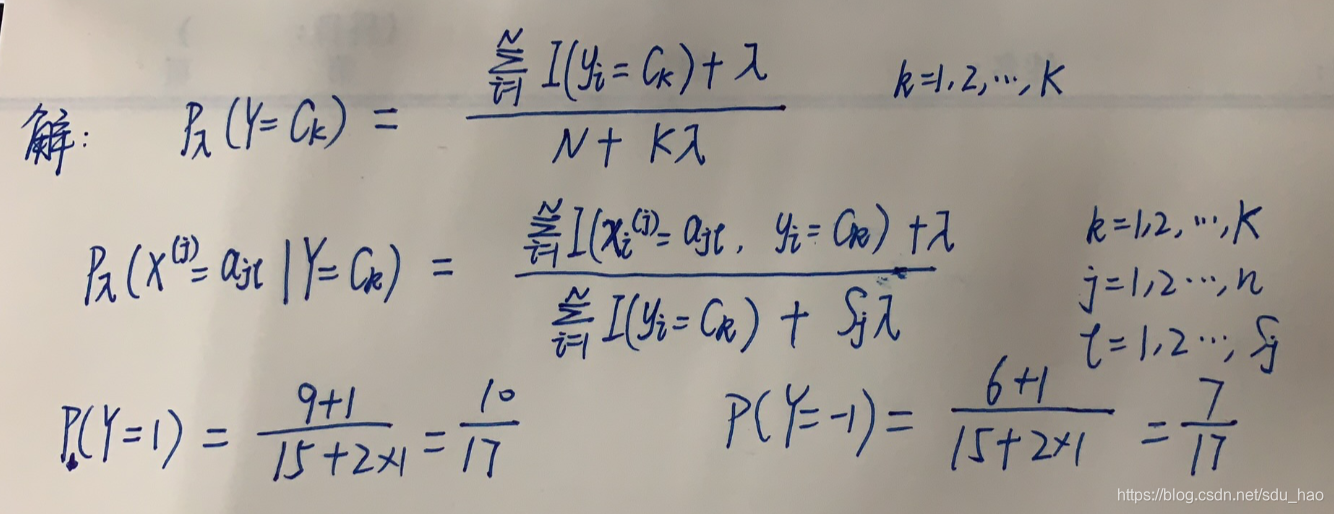

- 朴素贝叶斯算法
输入:训练数据集,其中
,
表示第i个样本的第j个特征,
表示第i个样本的第j个特征的取值集合(离散),
第j个特征可能取的第l个值
.
.实例特征向量x。
输出:实例x的类别
1)计算先验概率和条件概率(参数估计):
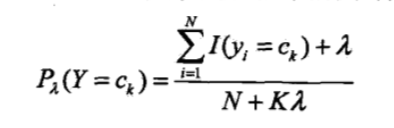
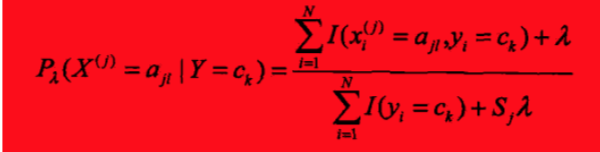
其中j=1,..,n; l = 1,...,;k = 1,...,K;
.
2)对于给定的实例,计算:
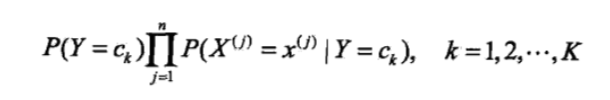
3)确定实例x的类别:
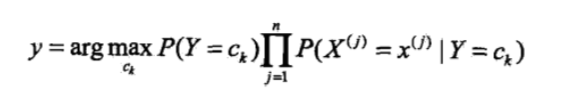
4. 朴素贝叶斯法的参数估计推导
在本节中对Y分布的估计,以及Y条件下X分布的估计,用到了极大似然估计和贝叶斯估计。这里通过对Y的分布的估计来推导一下极大似然估计和贝叶斯估计得到的结果。
- 问题描述
随机变量Y的分布是离散的,可能取值为,Y属于多项分布(对于每一个类别,Y的取值都有一个对应的概率
),
比如掷硬币,Y出现的结果有两种,正面和反面,正面出现的概率为,反面为
,
。如果只有两个结果,Y是二项分布,如果有K个结果,叫做多项分布。
Y的分布为:
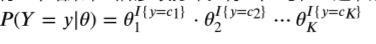
- 极大似然估计

- 贝叶斯估计

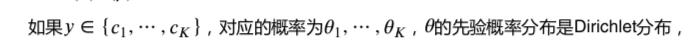
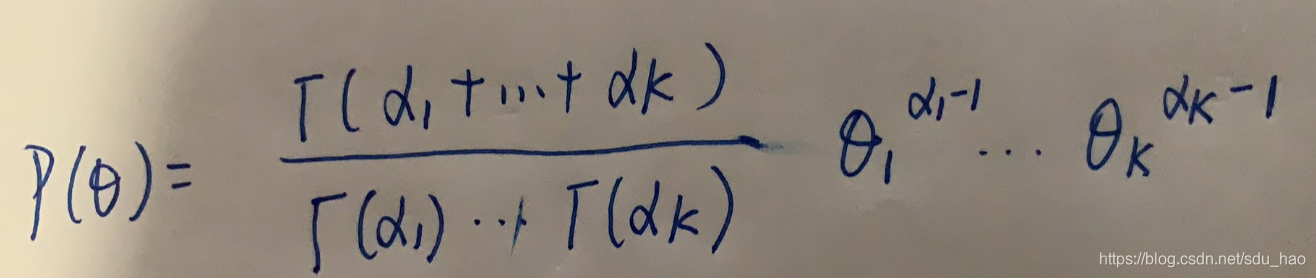


5. 小结
1)朴素贝叶斯是典型的生成学习方法。生成方法由训练数据学习联合概率分布P(X,Y),然后求得后验概率分布P(Y|X).具体来说通过训练数据学习条件概率分布P(X|Y)和先验概率分布P(Y),得到联合概率分布:
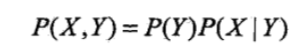
概率(参数)估计可以用极大似然估计或贝叶斯估计。
2)朴素贝叶斯法的基本假设是条件独立性:
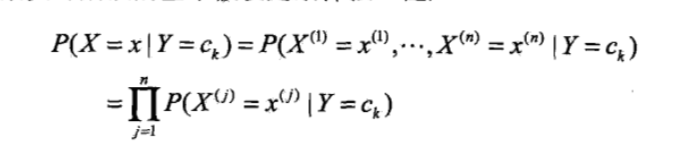
这是一个较强的假设。由于这一假设,模型包含的条件概率数量(参数数量)大大减少,朴素贝叶斯法的学习与预测大为简化。因而朴素贝叶斯法高效且易于实现。缺点是分类的性能不一定很高。
3)朴素贝叶斯法利用贝叶斯定理与学到的联合概率模型进行分类预测:
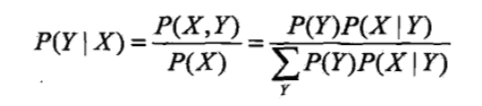
把输入x分到后验概率最大的类y:
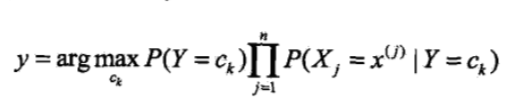
后验概率最大等价于0-1损失函数时的期望风险最小化。
这篇关于李航机器学习 | (6) 统计学习方法(第2版)笔记 --- 朴素贝叶斯法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




