计算第n个斐波那契数

计算第n个斐波那契数

斐波那契数列

​ 又称为“兔子数列”，最初该数列是为了解决兔子繁殖问题而提出的。问题如下：

​ 如果一对兔子每个月能剩一对兔子，而每对兔子在它出生后第三个月，又能开始生一对兔子。加入兔子没有死亡，由一对兔子开始，50个月之后会有多少对兔子。

​ 抽象成数学表达式既为：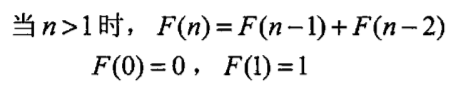

解决方案

​ 待选的解决方案有两种

• 我们可以根据计算机的特性，通过递推表达式来简单粗暴地求出从2到n所有的斐波那契数。当然我们要承担这一过程所消耗的庞大的时间成本
• 既然有递推表达式，我们可以求解这个带常系数的齐次二次线性递推式，来得到斐波那契数列的通式，进而在O(1)的成本下求出这个解
• 我们可以设计基于此等式的算法：
  当然，我们要知道如何高效的计算矩阵的乘方，这个方法还有点复杂，这里先不展开了，只能透露的是，这个方法的复杂度高效到只有O(log n)。但是耐不住我不会呀~~。

方案一：

第一种的实现比较简单，我们可以用很多种方法实现，递归也行，非递归也行

递归实现：

/** 
* @Description: 使用递归来实现斐波那契数列 
* @return: 返回第n个斐波那契数 
* @Author: Mr.Gao
* @Date: 2021/2/1 
*/
public int result(int n){if(n==1||n==2){return 1;}else{return result(n-1)+result(n-2);}
}

非递归实现：

/**
* @Description: 使用非递归实现斐波那契数列
* @return: 返回第n个斐波那契数
* @Author: Mr.Gao
* @Date: 2021/2/1
*/
public int result2(int n){int [] a=new int[n+1];a[1]=a[2]=1;for (int i = 3; i <= n; i++) {a[i]=a[i-1]+a[i-2];}return a[n];
}

• 这两种方案都限制于数值的大小，因为斐波那契数的增长速度是相当快的，int能表示的范围相比较来讲还是太小了。

复杂度分析：

• 在递归实现下，我们容易得知，移动次数：M(n)=M(n-1)+M(n-2)，M(1)=M(2)=1，使用反向替换法解这个式子，得知：基本操作的次数即为数列本身的值，我们依然要解出这个通解才能得知复杂度O（2的n次方）
• 在非递归的实现下，我们要遍历填充这个数组，所以我们的时间复杂度为O(n)

方案二：

​ 第二种方案要借助数学的力量，我们要求出斐波那契数列的解。我们根据之前离散里面学的解各种递推式的公式(见下方)。得我们的通式为：

​ 我们根据这个递归公式来解得每一项的值，但是这里有一个问题，计算机没办法表示无理数。我们这里有两种解决方案

• 可以借鉴Matlab中表示无理数的方式，将无理数看做是一个符号，然后再定义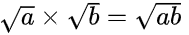之类的操作，就可以一定程度上计算这个公式
• 可以使用近似的方法
  这样我们就可以来计算，因为我们知道，斐波那契数都是整数，所以在结果上我们采取向上取整即可得到结果，但是同样在较大数字的计算下，会有误差。

Java代码：

/** 
* @Description: 使用数学的方法计算第n个斐波那契数 
* @return: 返回第n个斐波那契数 
* @Author: Mr.Gao
* @Date: 2021/2/2 
*/
public int result3(int n){double a=2.23606797;double b=1.61803398;double c=0.61803398;double temp=(Math.pow(b,n)-Math.pow(c,n))/a;int re=(int)(temp+0.5);return re;
}

• 这里我们使用近似的方法得到结果，至于将根号保存为另一种运算，等我水平高点儿再考虑吧~~

复杂度分析：

• 时间复杂度，这里并不是表面上看到的O(1)，因为在计算乘方的时候，我看了看Java底层的源码，我真的有点力不从心了，因为Java中这个方法中的n是可以为小数的，说实话，用手算一个数的小数次方我都算不出来，更别说用计算机实现了，到这里真的佩服Java的编写者，属实有些牛逼。这里我也不班门弄斧的去分析一下Java中这个pow方法的时间复杂度了
• 通过查看大神解析，这里我们放心假设，这个方法的时间复杂度为O(1)
• 以下为大神解析：