week7图的再议

problemA_TT 的魔法猫

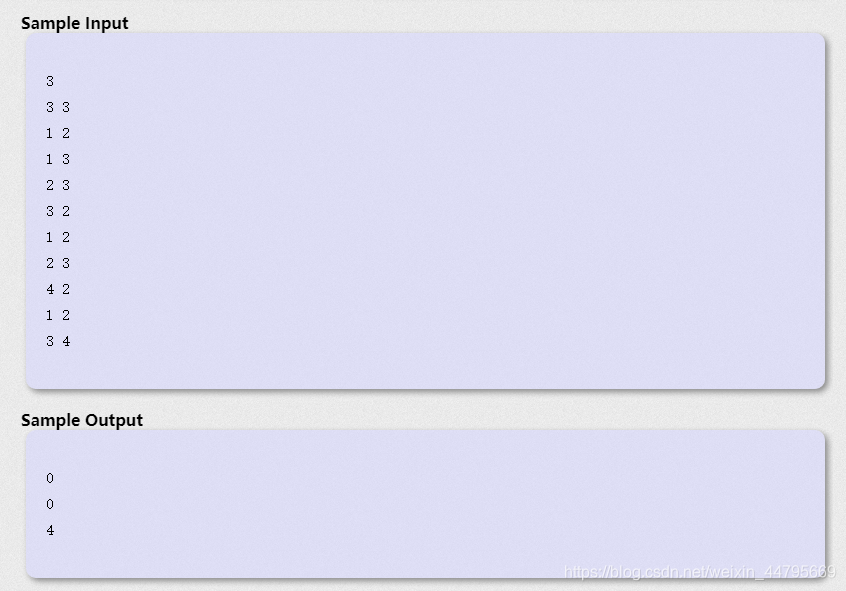
问题描述

问题分析

这是一个传递闭包的题目，即关系是可以传递的。用一个二维数组来描述是否比赛成绩已经明确。明确了a>b就复制那个点为1。输入完毕后直接开始循环。又由于只有当[i,k]和[k，j]都是1的情况下才能够确定[i,j]为1.所以只有[i,k]为1时才会有下一步操作。这就是对这个算法的剪枝。
总的来说，没有优化前复杂度为，n的三次方

代码

#include<iostream>
using namespace std;
//#include<stdio.h>
#include<algorithm>
int n,m;
int group;
int gread[501][501];
void game()
{for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){if(gread[i][k]==1){for(int j=1;j<=n;j++){gread[i][j]=max(gread[k][j],gread[i][j]);//min(gread[i][k],gread[k][j]) }}}}}
int main()
{//scanf("%d",&group);cin>>group;while(group--){//scanf("%d%d",&n,&m);cin>>n>>m;int a,b;for(int i=0;i<=n;i++){for(int j=0;j<=n;j++){gread[i][j]=0;//关系未知 }}for(int i=0;i<m;i++){//scanf("%d%d",&a,&b);cin>>a>>b;gread[a][b]=1;} game();int ans=0;for(int i=1;i<=n;i++){for(int j=i+1;j<=n;j++){if(gread[i][j]==0&&gread[j][i]==0)//关系未知ans++; }}cout<<ans<<endl; }return 0;} 

遇到的问题

1.第一遍剪枝不到位，导致了超时，当时那三层循环我把k放到最小的那个循环里面，并让一旦出现了i，j的值为1，就跳过。
2.循环时k，i的位置反了，样例过了，但是这个题最终的回答还是wrong answer。可能是迭代的顺序不对，导致有一些元素无法在适当的情况下更新。

problemB - TT 的旅行日记

问题描述

问题分析

dijikster算法，用最大堆（插入时用负的距离作为判断）来储存点。每次选取最大的点（其实就是dis最小的点）来展开更新。从堆中弹出一个点之后，遍历其所有能够到达的边，如果这个路径上的距离，即当前点的距离加上当前点到另一个点的距离，小于它原本所记录的距离，就更新这个点的距离。如果所能到达的点是从来没有到达过的点，就把点加入下一次可更新的范围里面。
开展两次上面的算法，得到每个点到s——起点的距离，再来一次得到所有点到e——终点的距离。然后在输入商业线的时候开始判断，商业线的一边端点到起点的距离加上另一边端点到终点的距离，再加上商业线的距离，看是否比不用商业险耗费小，如果是的话，就更新ans的值。
路径的输出靠的是pre数组，记录上一个站是哪一个，挨个回溯回去。存到一个数组里，在按序输出即可
复杂度：（n+m)*log(n)宽搜加堆排序

代码

#include<iostream>
using namespace std;
#include<algorithm>
#include<queue>
int n,s,e,m,k;
int tot1;
int dis1[10001],dis2[10001];
int pre1[10001],pre2[10001];
int vis[10001];
int shu[10001];
int zhan1,zhan2;
bool happend=false; 
priority_queue<pair<int,int> > que;
struct line1
{int x,y,z;int next;
}lines[250001];int head[10001];
void chushi()
{tot1=0;for(int i=0;i<n+1;i++){head[i]=-1;dis1[i]=100000;dis2[i]=100000;pre1[i]=0;pre2[i]=0;vis[i]=0;}
} 
void addline(int x,int y,int z)
{lines[tot1].x=x;lines[tot1].y=y;lines[tot1].z=z;lines[tot1].next=head[x];head[x]=tot1;tot1++;
}void dfs1(int s)
{que.push(make_pair(0,s));while(que.size()!=0)//!que.empty() {int xx=que.top().second;//跳出最需要操作的点 que.pop();if(vis[xx]==1) continue;vis[xx]=1;//cout<<"   dian="<<xx<<endl;for(int i=head[xx];i!=-1;i=lines[i].next){if(dis1[lines[i].y]>dis1[xx]+lines[i].z)//更新 {//cout<<"  y=  "<<lines[i].y<<endl;dis1[lines[i].y]=dis1[xx]+lines[i].z;pre1[lines[i].y]=xx;que.push(make_pair(-dis1[lines[i].y],lines[i].y));//入堆 }}}}
void dfs2(int e)
{que.push(make_pair(0,e));while(que.size()!=0)//!que.empty() {int xx=que.top().second;//跳出最需要操作的点 que.pop();if(vis[xx]==2) continue;vis[xx]=2;//cout<<"   dian="<<xx<<endl;for(int i=head[xx];i!=-1;i=lines[i].next){//cout<<"  y=  "<<lines[i].y<<endl;if(dis2[lines[i].y]>dis2[xx]+lines[i].z)//更新 {//cout<<"被选中的    y="<<lines[i].y<<endl;dis2[lines[i].y]=dis2[xx]+lines[i].z;pre2[lines[i].y]=xx;que.push(make_pair(-dis2[lines[i].y],lines[i].y));//入堆 }}} 
}int main()
{int x,y,z;int ans;while(cin>>n>>s>>e){chushi();cin>>m;for(int i=0;i<m;i++){cin>>x>>y>>z;addline(x,y,z);addline(y,x,z);}dis1[s]=0;dis2[e]=0;dfs1(s);dfs2(e);ans=dis1[e];zhan1=zhan2=0;int number;cin>>k;for(int i=0;i<k;i++){cin>>x>>y>>z;if(ans>dis1[x]+dis2[y]+z)//&&(dis1[x]!=0||x==s)&&(dis2[y]!=0||y==e){ans=dis1[x]+dis2[y]+z;zhan1=x;zhan2=y;}else if(ans>dis2[x]+dis1[y]+z){ans=dis2[x]+dis1[y]+z;zhan1=y;zhan2=x;}}if(happend)cout<<endl;//最后一个例子不输出回车 else happend=true; int i,j;if(zhan1==0){i=s;while(i!=e){cout<<i<<" ";i=pre2[i];}cout<<i<<endl;cout<<"Ticket Not Used"<<endl;cout<<ans<<endl;}else{i=zhan2;j=zhan1;int mm=1;while(j!=s){shu[mm]=j;mm++;j=pre1[j];if(j==pre1[j]){break;}}shu[mm]=s;while(mm!=0){cout<<shu[mm]<<" ";mm--;}while(i!=e){cout<<i<<" ";i=pre2[i];}cout<<i<<endl;cout<<zhan1<<endl;cout<<ans<<endl;}}return 0;} 

遇到的问题

1.循环不知道为什么停止不了，最后在while中又加了一个判断条件re
2.前期没有用最大堆来判断操作哪个点，是直接深搜了，导致超时
3.没有理解完题目输出意思，每个数据输出之间有个回车，不是每个数据输出后都有一个回车，pe了

problemC - TT 的美梦

问题描述

问题分析

这个问题，由于会有负环的产生（w不会一直为正，dis可能会越来越小），比起上面的算法这里多了一些东西，
首先，这个算法里点是可以重复入队的，只要它现在不在队内，它就可以再次入队。
其次就是对于负环的判断，虽然是想要产生最小生成树，但是如果出现了负环很明显和目标结果不一样。这个时候这个点就没法再走下去了，因为不会有最小的距离只会有更小的距离。而一旦n个点中选取边来生成树，有且只有n-1条边，一旦边数超过了n-1一定是出现了环，这个点肯定在那个负环上面，下一次就不能够再次对这个点进行扩展了。
输入数据后，先对其数据转换成图的摸样，将权重直接转换成边的大小。构建有向图。用上述算法开展遍历，当该点不是负环可以继续计算，到该点的税钱少则更新钱数，如果这个点当前不在队列里面，进队。然后再挨个进行扩展即可。

代码

#include<iostream>
using namespace std; 
#include<algorithm>
#include<queue>
int T,N,M,Q,P;
int A,B;
int a[500];//权重 
struct line
{int to,next,w;
}lines[100001];
int head[500];//下标 
int vis[500];//是否到达 
int dis[500];//最小税费 
int ceng[500];//第几个 
int sixh[500];//负环 
int tot;//边的下标 
void init()
{tot=0;for(int i=1;i<=N;i++){head[i]=-1;vis[i]=0;dis[i]=100000;sixh[i]=0;ceng[i]=0;a[i]=0;}
}
void addline(int u,int v,int wei)
{lines[tot].to=v;lines[tot].w=wei;lines[tot].next=head[u];//cout<<"line "<<tot<<"    "<<lines[tot].to<<"    "<<lines[tot].w<<"    "<<lines[tot].next<<endl;head[u]=tot;tot++;
}
queue<int> que;
void tax()
{que.push(1);dis[1]=0;while(que.size()!=0)//!que.empty() {int xx=que.front();que.pop();vis[xx]=0;//释放 ,允许再次到达 for(int i=head[xx];i!=-1;i=lines[i].next){if(sixh[xx]==1) continue;//负环就不用再走 if(dis[lines[i].to]>dis[xx]+lines[i].w)//更新 {dis[lines[i].to]=dis[xx]+lines[i].w;ceng[lines[i].to]=ceng[xx]+1;if(ceng[lines[i].to]>=N)//肯定出现过环 {sixh[lines[i].to]=1;//xunhuan(lines[i].to);}if(vis[lines[i].to]==0){que.push(lines[i].to);//入队 vis[lines[i].to]=1; }}}}
}
int main()
{scanf("%d",&T); for(int i=1;i<=T;i++){scanf("%d",&N);init();for(int j=1;j<=N;j++){scanf("%d",&a[j]);}scanf("%d",&M);for(int j=1;j<=M;j++){scanf("%d%d",&A,&B);int t=a[B]-a[A];addline(A,B,t*t*t);}tax();printf("Case %d:\n",i);scanf("%d",&Q);for(int j=1;j<=Q;j++){scanf("%d",&P);if(sixh[P]==1||dis[P]==100000||dis[P]<3)//{cout<<"?"<<endl;}else{cout<<dis[P]<<endl;}}}return 0;
}

遇到的问题

1.初始化早了，就是写的时候没有注意，还有一些后来加的数组忘记初始化，层数（看上去不是很重要，但是某些值很重要）
2.负环判断那里最开始的想法是这个点是负环，其它能由这个点到达的地方也是负环（因为继续下去总会负环的）然后就一直错。最后改成这个点的层数超过N了，就只有这个点是负环，和其他点无关。
3.复杂度还不太会算，一般的深搜是n+m但是这个点不一定只经历一次，应该比深搜复杂度高，但是具体高多少不确定。