codeforces每日5题(均1600)-第三十三天

Alyona and Spreadsheet

题面翻译

给出一个n*m的矩阵

对于第j列，如果满足$\forall i\in [1,n-1],a_{i,j}\le a_{i+1,j}$，则称这一列是不下降的。

k次询问，问如果只保留矩阵的第L~R行，矩阵中是否存在不下降的一列。

题目描述

During the lesson small girl Alyona works with one famous spreadsheet computer program and learns how to edit tables.

Now she has a table filled with integers.

The table consists of $n$ rows and $m$ columns.

By $a_{i,j}$ we will denote the integer located at the $i$ -th row and the $j$ -th column.

We say that the table is sorted in non-decreasing order in the column $j$ if $a_{i,j}<=a_{i+1,j}$ for all $i$ from $1$ to $n-1$ .

Teacher gave Alyona $k$ tasks.

For each of the tasks two integers $l$ and $r$ are given and Alyona has to answer the following question: if one keeps the rows from $l$ to $r$ inclusive and deletes all others, will the table be sorted in non-decreasing order in at least one column?

Formally, does there exist such $j$ that $a_{i,j}<=a_{i+1,j}$ for all $i$ from $l$ to $r-1$ inclusive.

Alyona is too small to deal with this task and asks you to help!

输入格式

The first line of the input contains two positive integers $n$ and $m$ ( $1<=n\cdot m<=100000$ ) — the number of rows and the number of columns in the table respectively.

Note that your are given a constraint that bound the product of these two integers, i.e. the number of elements in the table.

Each of the following $n$ lines contains $m$ integers.

The $j$ -th integers in the $i$ of these lines stands for $a_{i,j}$ ( $1<=a_{i,j}<=10^9$ ).

The next line of the input contains an integer $k$ ( $1<=k<=100000$ ) — the number of task that teacher gave to Alyona.

The $i$ -th of the next $k$ lines contains two integers $l_i$ and $r_i$ ( $1<=l_i<=r_i<=n$ ).

输出格式

Print “Yes” to the $i$ -th line of the output if the table consisting of rows from $l_i$ to $r_i$ inclusive is sorted in non-decreasing order in at least one column. Otherwise, print “No”.

样例 #1

样例输入 #1

5 4
1 2 3 5
3 1 3 2
4 5 2 3
5 5 3 2
4 4 3 4
6
1 1
2 5
4 5
3 5
1 3
1 5

样例输出 #1

Yes
No
Yes
Yes
Yes
No

提示

In the sample, the whole table is not sorted in any column.

However, rows 1–3 are sorted in column $1$ , while rows 4–5 are sorted in column $3$ .

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
typedef long long ll;
int n,m,k,last[N],reach[N],lastre[N],ans[N],kk,l,r;
int main(){memset(ans,0x3f,sizeof(ans));memset(last,0x3f,sizeof(last));cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){scanf("%d",&k);if(k<last[j]) reach[j]=i;else reach[j]=lastre[j];lastre[j]=reach[j];last[j]=k;ans[i]=min(ans[i],reach[j]);}}cin>>kk;while(kk--){scanf("%d%d",&l,&r);cout<<(ans[r]<=l?"Yes":"No")<<endl;}return 0;
}

Timofey and a tree

题面翻译

一棵无根树中各个节点被染上了一种颜色c[i]

现在让你选择一个点作为根节点，使得这个根节点的所有儿子满足以该儿子节点的作为根的子树中所有点颜色均相同（不同儿子为根的子树颜色可以不同）。

题目描述

Each New Year Timofey and his friends cut down a tree of $n$ vertices and bring it home.

After that they paint all the $n$ its vertices, so that the $i$ -th vertex gets color $c_i$ .

Now it’s time for Timofey birthday, and his mother asked him to remove the tree.

Timofey removes the tree in the following way: he takes some vertex in hands, while all the other vertices move down so that the tree becomes rooted at the chosen vertex.

After that Timofey brings the tree to a trash can.

Timofey doesn’t like it when many colors are mixing together.

A subtree annoys him if there are vertices of different color in it.

Timofey wants to find a vertex which he should take in hands so that there are no subtrees that annoy him.

He doesn’t consider the whole tree as a subtree since he can’t see the color of the root vertex.

A subtree of some vertex is a subgraph containing that vertex and all its descendants.

Your task is to determine if there is a vertex, taking which in hands Timofey wouldn’t be annoyed.

输入格式

The first line contains single integer $n$ ( $2<=n<=10^5$ ) — the number of vertices in the tree.

Each of the next $n-1$ lines contains two integers $u$ and $v$ ( $1<=u,v<=n$ , $u\ne v$ ), denoting there is an edge between vertices $u$ and $v$ .

It is guaranteed that the given graph is a tree.

The next line contains $n$ integers $c_1,c_2,...,c_n$ ( $1<=c_i<=10^5$ ), denoting the colors of the vertices.

输出格式

Print “NO” in a single line, if Timofey can’t take the tree in such a way that it doesn’t annoy him.

Otherwise print “YES” in the first line.

In the second line print the index of the vertex which Timofey should take in hands.

If there are multiple answers, print any of them.

样例 #1

样例输入 #1

4
1 2
2 3
3 4
1 2 1 1

样例输出 #1

YES
2

样例 #2

样例输入 #2

3
1 2
2 3
1 2 3

样例输出 #2

YES
2

样例 #3

样例输入 #3

4
1 2
2 3
3 4
1 2 1 2

样例输出 #3

NO

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
typedef long long ll;
int n,a[N],b[N],c[N],k=0,s[N];
int main(){scanf("%d",&n);for(int i=1;i<=n-1;i++) scanf("%d%d",&a[i],&b[i]);for(int i=1;i<=n;i++) scanf("%d",&c[i]);for(int i=1;i<=n-1;i++){if(c[a[i]]!=c[b[i]]){k++;s[a[i]]++,s[b[i]]++;}}for(int i=1;i<=n;i++){if(s[i]==k){printf("YES\n%d\n",i);return 0;}}puts("NO");return 0;
}

An impassioned circulation of affection

题面翻译

给你一个由小写字母构成的字符串.  
有$q$个询问,每个询问给出数字$m$和小写字母$c$,你可以任意地修改字符串中的$m$个字符,求最多能够使字符串中含有多少个连续相同的字母$c$.  
每个询问各自独立.

题目描述

Nadeko’s birthday is approaching!

As she decorated the room for the party, a long garland of Dianthus-shaped paper pieces was placed on a prominent part of the wall.

Brother Koyomi will like it!

Still unsatisfied with the garland, Nadeko decided to polish it again.

The garland has $n$ pieces numbered from $1$ to $n$ from left to right, and the $i$ -th piece has a colour $s_i$ , denoted by a lowercase English letter.

Nadeko will repaint at most $m$ of the pieces to give each of them an arbitrary new colour (still denoted by a lowercase English letter).

After this work, she finds out all subsegments of the garland containing pieces of only colour $c$ — Brother Koyomi’s favourite one, and takes the length of the longest among them to be the Koyomity of the garland.

For instance, let’s say the garland is represented by “kooomo”, and Brother Koyomi’s favourite colour is “o”.

Among all subsegments containing pieces of “o” only, “ooo” is the longest, with a length of $3$ .

Thus the Koyomity of this garland equals $3$ .

But problem arises as Nadeko is unsure about Brother Koyomi’s favourite colour, and has swaying ideas on the amount of work to do.

She has $q$ plans on this, each of which can be expressed as a pair of an integer $m_i$ and a lowercase letter $c_i$ , meanings of which are explained above.

You are to find out the maximum Koyomity achievable after repainting the garland according to each plan.

输入格式

The first line of input contains a positive integer $n$ ( $1<=n<=1500$ ) — the length of the garland.

The second line contains $n$ lowercase English letters $s_1{s}_2...s_n$ as a string — the initial colours of paper pieces on the garland.

The third line contains a positive integer $q$ ( $1<=q<=200000$ ) — the number of plans Nadeko has.

The next $q$ lines describe one plan each: the $i$ -th among them contains an integer $m_i$ ( $1<=m_i<=n$ ) — the maximum amount of pieces to repaint, followed by a space, then by a lowercase English letter $c_i$ — Koyomi’s possible favourite colour.

输出格式

Output $q$ lines: for each work plan, output one line containing an integer — the largest Koyomity achievable after repainting the garland according to it.

样例 #1

样例输入 #1

6
koyomi
3
1 o
4 o
4 m

样例输出 #1

3
6
5

样例 #2

样例输入 #2

15
yamatonadeshiko
10
1 a
2 a
3 a
4 a
5 a
1 b
2 b
3 b
4 b
5 b

样例输出 #2

3
4
5
7
8
1
2
3
4
5

样例 #3

样例输入 #3

10
aaaaaaaaaa
2
10 b
10 z

样例输出 #3

10
10

提示

In the first sample, there are three plans:

• In the first plan, at most $1$ piece can be repainted.

Repainting the “y” piece to become “o” results in “kooomi”, whose Koyomity of $3$ is the best achievable;

• In the second plan, at most $4$ pieces can be repainted, and “oooooo” results in a Koyomity of $6$ ;
• In the third plan, at most $4$ pieces can be repainted, and “mmmmmi” and “kmmmmm” both result in a Koyomity of $5$ .

#include<bits/stdc++.h>
using namespace std;
const int N=2e3+10;
typedef long long ll;
int n,m,k,p[N][27];
char s[1600];
char ch;
int main(){scanf("%d",&n);scanf("%s",s+1);cin>>m;for(register int i=1;i<=n;i++){for(register int j=0;j<26;j++){p[i][j]+=p[i-1][j];}++p[i][s[i]-'a'];}for(register int i=1;i<=m;i++){int l=1,r=1,ans=0;scanf("%d %c",&k,&ch);while(r<=n){while(p[r][ch-'a']-p[l-1][ch-'a']+k<r-l+1) ++l;ans=max(ans,r-l+1);++r;}printf("%d\n",ans);}return 0;
}

Multi-judge Solving

题面翻译

DecoForces 上存在 $n$ 个问题，难度为 $a_1,a_2,a_3\cdots a_n$，你已经做到了难度最高为 $k$ 的题目。

现在存在两种 OJ，一个是上述的 DecoForces，一个是其他的 OJ。如果 DecoForces 没有某一难度的题目，那其他 OJ 上一定有。

假设你现在做到了难度为 $k$ 的题目，那你下次可以做 $a_i\le 2\times k$ 的题目，做完之后 $k$ 就要更新为你做过最难的题目。

你至少要在其他 OJ 上做几道题？

Translate By Aw顿顿

题目描述

Makes solves problems on Decoforces and lots of other different online judges.

Each problem is denoted by its difficulty — a positive integer number.

Difficulties are measured the same across all the judges (the problem with difficulty $d$ on Decoforces is as hard as the problem with difficulty $ d $ on any other judge).

Makes has chosen $n$ problems to solve on Decoforces with difficulties $a_1,a_2,...,a_n$ .

He can solve these problems in arbitrary order.

Though he can solve problem $i$ with difficulty $a_i$ only if he had already solved some problem with difficulty 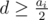(no matter on what online judge was it).

Before starting this chosen list of problems, Makes has already solved problems with maximum difficulty $k$ .

With given conditions it’s easy to see that Makes sometimes can’t solve all the chosen problems, no matter what order he chooses.

So he wants to solve some problems on other judges to finish solving problems from his list.

For every positive integer $y$ there exist some problem with difficulty $y$ on at least one judge besides Decoforces.

Makes can solve problems on any judge at any time, it isn’t necessary to do problems from the chosen list one right after another.

Makes doesn’t have too much free time, so he asked you to calculate the minimum number of problems he should solve on other judges in order to solve all the chosen problems from Decoforces.

输入格式

The first line contains two integer numbers $n$ , $k$ ( $1<=n<=10^3$ , $1<=k<=10^9$ ).

The second line contains $n$ space-separated integer numbers $a_1,a_2,...,a_n$ ( $1<=a_i<=10^9$ ).

输出格式

Print minimum number of problems Makes should solve on other judges in order to solve all chosen problems on Decoforces.

样例 #1

样例输入 #1

3 3
2 1 9

样例输出 #1

1

样例 #2

样例输入 #2

4 20
10 3 6 3

样例输出 #2

0

提示

In the first example Makes at first solves problems 1 and 2.

Then in order to solve the problem with difficulty 9, he should solve problem with difficulty no less than 5.

The only available are difficulties 5 and 6 on some other judge. Solving any of these will give Makes opportunity to solve problem 3.

In the second example he can solve every problem right from the start.

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
typedef long long ll;
ll n,k,a[N],ans=0;
int main(){cin>>n>>k;for(int i=1;i<=n;i++) scanf("%lld",&a[i]);sort(a+1,a+1+n);for(int i=1;i<=n;i++){while(a[i]>2*k) ans++,k*=2;k=max(k,a[i]);}cout<<ans<<endl;return 0;
}

Preparing for Merge Sort

题面翻译

Ivan有一个包含$n$个不同整数的数组。他计划将这个数组变成升序的。Ivan喜欢归并排序，所以他想将这个数组变成一个或多个升序数组，之后将它们合并。

他用如下的方式将原数组变成一个或多个升序数组：

Ivan将对数组进行若干次迭代，直到数组中所有元素都被放入新数组。

对于每次迭代，Ivan将依次从左到右遍历每个还未放入新数组中的元素。如果某个元素是该次迭代中的第一个元素，那么它将会放入属于本次迭代的新数组中。如果某个元素不是该次迭代中的第一个元素，那么当且仅当它比属于本次迭代的新数组中最后一个数大时，它将被放入属于本次迭代的新数组的末尾。

更具体的，对于一串数$[1,3,2,5,4]$，第一次迭代将取出$[1,3,5]$这$3$个元素，第二次迭代将取出$[2,4]$这$2$个元素，因为它们是严格递增的。

输入格式：第一行一个数$n(n\le 2\times 10^5)$，表示数组中元素的个数。第二行$n$个整数，表示数组中的每个元素。

输出格式：每行若干个数，第$i$行表示属于第$i$次迭代的新数组。

题目描述

Ivan has an array consisting of $n$ different integers.

He decided to reorder all elements in increasing order. Ivan loves merge sort so he decided to represent his array with one or several increasing sequences which he then plans to merge into one sorted array.

Ivan represent his array with increasing sequences with help of the following algorithm.

While there is at least one unused number in array Ivan repeats the following procedure:

• iterate through array from the left to the right;
• Ivan only looks at unused numbers on current iteration;
• if current number is the first unused number on this iteration or this number is greater than previous unused number on current iteration, then Ivan marks the number as used and writes it down.

For example, if Ivan’s array looks like [1, 3, 2, 5, 4] then he will perform two iterations.

On first iteration Ivan will use and write numbers [1, 3, 5], and on second one — [2, 4].

Write a program which helps Ivan and finds representation of the given array with one or several increasing sequences in accordance with algorithm described above.

输入格式

The first line contains a single integer n KaTeX parse error: Expected '}', got 'EOF' at end of input: ( 1<=n<=2·10^{ ) — the number of elements in Ivan’s array.

The second line contains a sequence consisting of distinct integers $a_1,a_2,...,a_n$ ( $1<=a_i<=10^9$ ) — Ivan’s array.

输出格式

Print representation of the given array in the form of one or more increasing sequences in accordance with the algorithm described above. Each sequence must be printed on a new line.

样例 #1

样例输入 #1

5
1 3 2 5 4

样例输出 #1

1 3 5 
2 4

样例 #2

样例输入 #2

4
4 3 2 1

样例输出 #2

4 
3 
2 
1

样例 #3

样例输入 #3

4
10 30 50 101

样例输出 #3

10 30 50 101

#include<bits/stdc++.h>
#pragma GCC optimize(2)
using namespace std;
const int N=1e6+10;
typedef long long ll;
int n,k,p,a[N];
vector<int> v[N];
int main(){cin>>n;for(int i=1;i<=n;i++){scanf("%d",&k);p=lower_bound(a,a+n+1,k)-a-1;a[p]=k;v[p].push_back(k);}for(int i=n;i>=0&&v[i].size();i--,puts("")){for(int j=0;j<v[i].size();j++){printf("%d ",v[i][j]);}}return 0;
}