本文主要是介绍Codeforces Round #465 (Div. 2) D. Fafa and Ancient Alphabet,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目:
题目分析:
n为a串和b串的长度,m为set的大小,a串和b串中为0的位置可以填1-m中的任意一个数,让你求a串字典序大于b串的概率p/q(mod 1000000007)。
为了这道题,调了2个小时的bug竟然发现是数组大小没开够……
p/q好求,就是简单的遍历加上计算,但是求逆元的话我给忘了,下面总结一下分数求逆元。
首先说一下逆元。
若a*x%mode=1,则x是a的逆元。
通过式子,我们可以联想到扩展欧几里得:a*x+mode*y=1,若式子有解,要求gcd(a,mode)=1。
扩展欧几里得算法如下(是辗转相除法的扩展):
void e_gcd(ll a,ll b,ll &x,ll &y)
{
if(b==0)
{
x=1;
y=0;
return ;
}
else
{
e_gcd(b,a%b,x,y);
ll tmp=x;
x=y;
y=tmp-a/b*y;
return ;
}
}
最后求出来的结果可能为负,要加上:x=(x%mode+mode)%mode;
最后一个要注意的点,也是我错的点,就是注意a,b串中0位置的个数最大可能为2*maxn,而不是maxn
附上代码:
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<iostream>
using namespace std;
typedef long long ll;
const int maxn=1e5+10;
ll string_a[maxn],string_b[maxn];
const long long mode=1e9+7;
ll r[maxn];
ll pow[2*maxn];
void init(long long m)
{
pow[0]=1;
for(long long i=1;i<2*maxn;i++)
pow[i]=pow[i-1]*m%mode;
return;
}
void e_gcd(ll a,ll b,ll &x,ll &y)
{
if(b==0)
{
x=1;
y=0;
return ;
}
else
{
e_gcd(b,a%b,x,y);
ll tmp=x;
x=y;
y=tmp-a/b*y;
return ;
}
}
int main()
{
ll n,m,cnt=0;
scanf("%lld%lld",&n,&m);
for(int i=0;i<n;i++)
scanf("%lld",&string_a[i]);
for(int i=0;i<n;i++)
scanf("%lld",&string_b[i]);
memset(r,0,sizeof(r));
r[n-1]=0;
for(int i=n-2;i>=0;i--)
{
if(string_a[i+1]==0)
r[i]++;
if(string_b[i+1]==0)
r[i]++;
r[i]+=r[i+1];
}
cnt=r[0];
if(string_a[0]==0)
cnt++;
if(string_b[0]==0)
cnt++;
init(m);
ll s_equal=1,ans=0;
for(int i=0;i<n;i++)
{
if(string_a[i]==0)
{
if(string_b[i]==0)
{
ans+=(((s_equal*(m*(m-1)/2%mode)%mode)*pow[r[i]])%mode);
ans%=mode;
s_equal*=m;
s_equal%=mode;
}
else
{
ans+=(((s_equal*(max(m-string_b[i],(ll)0))%mode)*pow[r[i]])%mode);
ans%=mode;
}
}
else
{
if(string_b[i]==0)
{
ans+=(((s_equal*(min(string_a[i]-1,m))%mode)*pow[r[i]])%mode);
ans%=mode;
}
else
{
if(string_a[i]==string_b[i])
continue;
else if(string_a[i]>string_b[i])
{
ans+=(s_equal*pow[r[i]]%mode);
ans%=mode;
break;
}
else
break;
}
}
}
long long q=pow[cnt];
long long x,y;//x为q的逆元
e_gcd(q,mode,x,y);
x=(x%mode+mode)%mode;
ans=ans*x%mode;
cout<<ans<<endl;
}
//错误估计了数组的大小
这篇关于Codeforces Round #465 (Div. 2) D. Fafa and Ancient Alphabet的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!
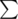 to write on the walls of the temples. Fafa and Fifa went to one of the temples and found two non-empty words
to write on the walls of the temples. Fafa and Fifa went to one of the temples and found two non-empty words 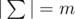 , i. e. there were
, i. e. there were 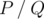 , where
, where 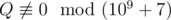 . Print as the answer the value
. Print as the answer the value 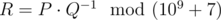 , i. e. such a non-negative integer less than
, i. e. such a non-negative integer less than 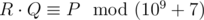 , where
, where 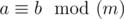 means that
means that 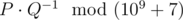 , where
, where 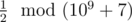 , that is
, that is 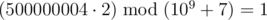 .
.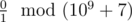 , that is
, that is 





