本文主要是介绍活图的峰值检测函数(1),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
活图(中文版活图ver8.1现在是常州微识自动化科技有限公司产品之一http://www.microverify.com/col.jsp?id=114)的数值函数中,有关峰值检测的函数有10种,它们是:
1. peak_xiyi([ix],[iy],[ox],[oy],对象0-2)
函数的功能和各参数的含义是:
功能:检出峰值
公式:peak_xiyi([ix],[iy],[ox],[oy],对象(0-2))
说明:对输入数值组[ix]],[iy]定义的连续曲线,检出其峰值(极值),并存放在数值组[ox],[oy].另 外,检出的峰值对象可由参数指定成极大极小的三种组合,曲线的始点和终点无条件被作为峰值检出.
将检出峰值用线连起来,既是包络线.
[ix],[iy] 曲线的XY坐标输入数值组([ix]为自然数时可用@代替)
[ox],[oy] 峰值坐标输出数值组
对象(0-2) 峰值检出对象,0:极大极小双方 1:极大 2:极小
例 :peak_xiyi([1],[2],[3],[4],1)
在活图数式窗口中的具体实施例子如图1
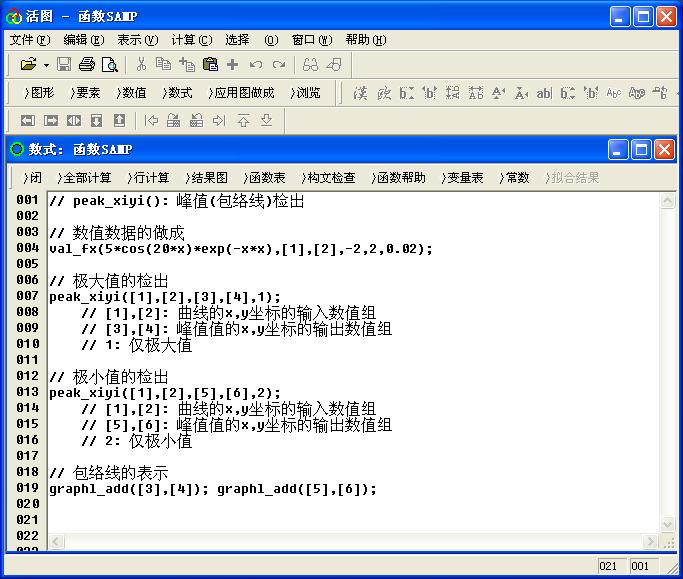
图1
对应结果图如图2
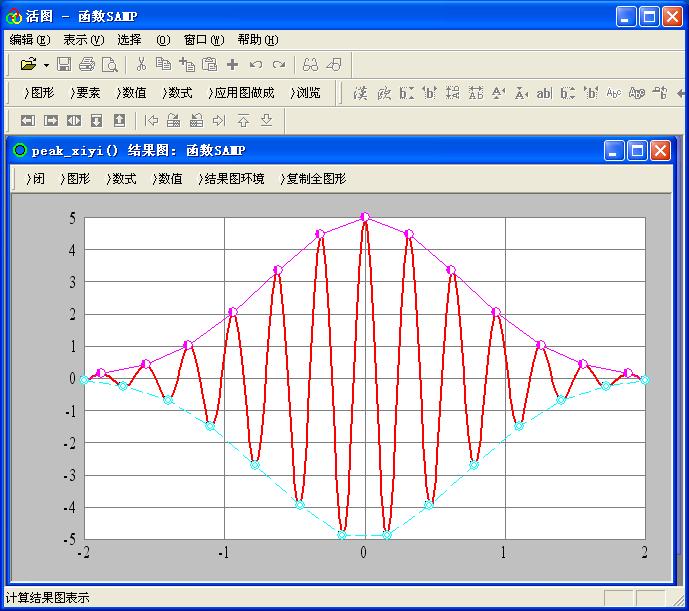
图2
对应活图数据窗口如图3
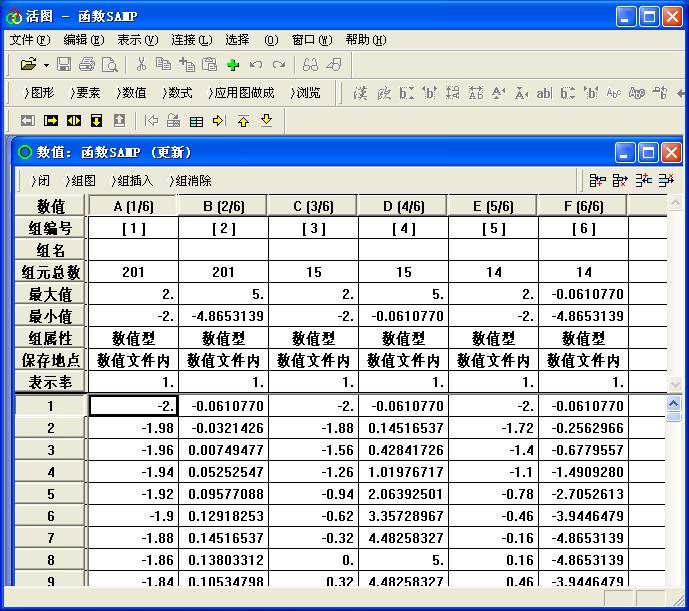
图3
2. peak1_xiyi([ix],[iy],[ox],[oy], 对象0-2,yd)
函数的功能和各参数的含义是:
功能:检出峰值(带阈值)
公式:peak1_xiyi([ix],[iy],[ox],[oy],对象(0-2),yd)
说明:带阈值条件的峰值检出,对输入数值组[ix],[iy]定义的连续曲线,仅检出绝对值不小于给定阈值yd的峰值(极值),并存放在数值组[ox],[oy].另外,检出的峰值对象可由参数指定成极大极小的三种组合,曲线的始点和终点无条件被作为峰值检出.
将检出峰值用线连起来,既是包络线.
[ix],[iy] 曲线的XY坐标输入数值组([ix]为自然数时可用@ 代替)
[ox],[oy] 峰值坐标输出数值组
对象(0-2) 峰值检出对象,0:极大极小双方 1:极大 2:极小
yd 指定的阈值,小于此阈值的峰值不被检出
例 :peak1_xiyi([1],[2],[3],[4],1,3)
在活图数式窗口中的具体实施例子如图4
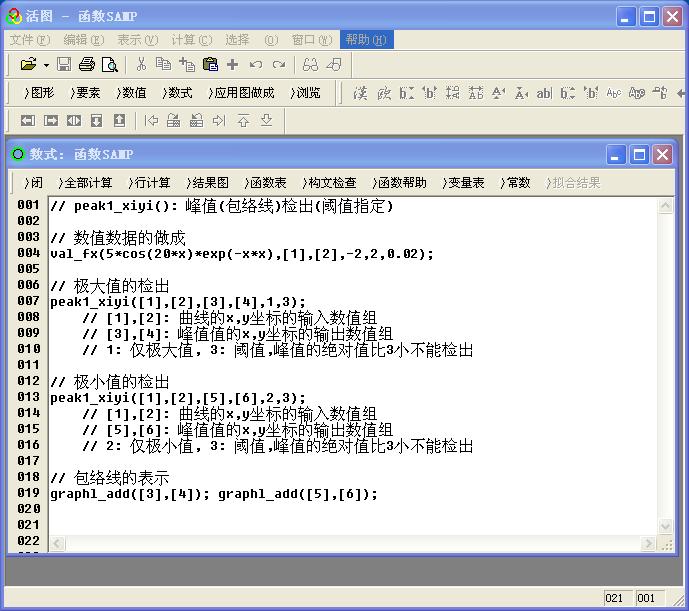
图4
对应结果图如图5
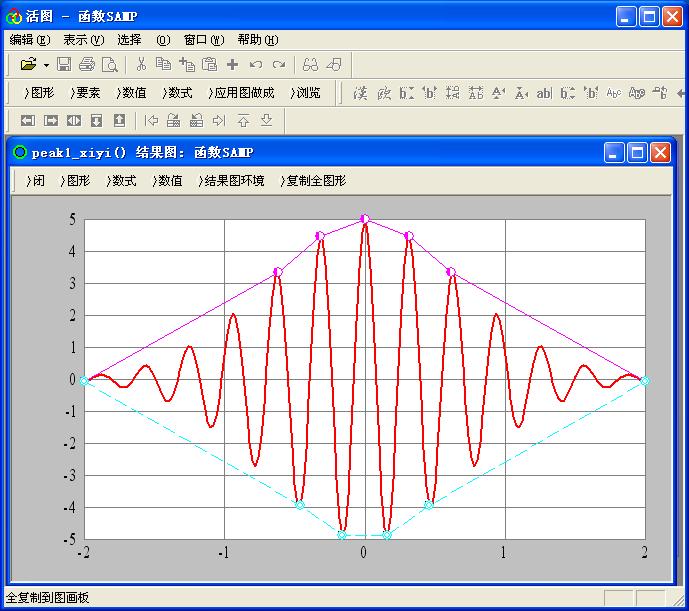
图5
对应活图数据窗口如图6

图6
3. Peak2_xiyi([ix],[iy],[ox],[oy], 对象0-2,x,y)
函数的功能和各参数的含义是:
功能:检出峰值(带滞后值)
公式:peak2_xiyi([ix],[iy],[ox],[oy],对象(0-2),x,y)
说明:带滞后值条件的峰值检出,对输入数值组[ix],[iy]定义的连续曲线,检出满足滞后条件的峰值(极值),并返回该值.另外,检出的峰值对象可由参数指定成极大极小的三种组合,曲线的始点和终点无条件被作为峰值检出.
[ix],[iy] 曲线的XY坐标输入数值组([ix]为自然数时可用@代替)
对象(0-2) 峰值检出对象,0:极大极小双方 1:极大 2:极小
[ox],[oy] 峰值坐标输出数值组
x,y 指定的X和Y方向的滞后值,前后峰值距离小于x和y值的峰值不被检出
例 :peak2_xiyi([1],[2],[3],[4],1,0.06,2.5)
在活图数式窗口中的具体实施例子如图7
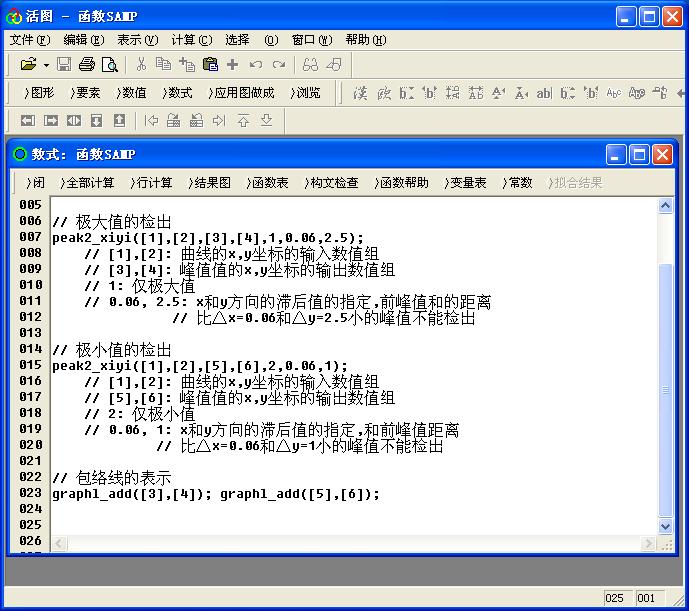
图7
对应结果图如图8
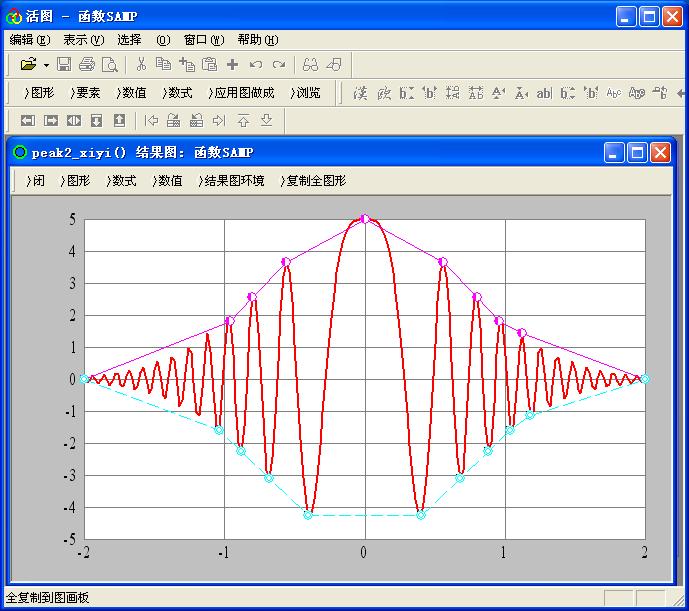
图8
对应活图数据窗口如图9
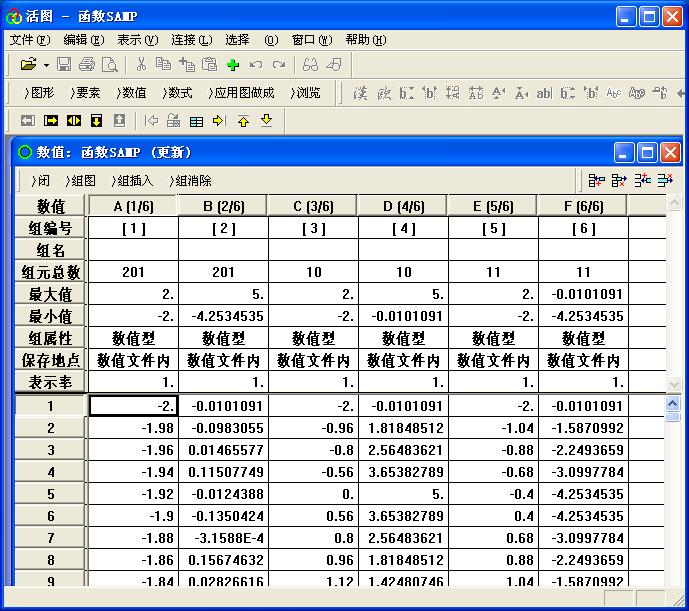
图9
这篇关于活图的峰值检测函数(1)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


