对K，要不起

KNN算法是一种分类算法，和Kmeans是看起来像但可以说没啥关系。KNN的数据集都是带label的（监督学习），整个分类过程类似于一种投票机制。

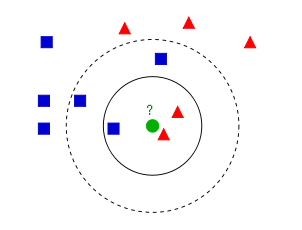
这里KNN的K指的是当我们给样本x分类的时候，我们就从数据集里找跟x距离最近的k个数据点，然后选k个数据点中类别最多的类给x。比如上图：k的取值是能直接决定分类效果的，当k取3时，绿点应被归为红三角（2 >1）；当k取5是，绿点又被归为蓝方块（3>2）

KNN没有明显的训练过程，是一种基于记忆的学习。它和Kmeans唯一的共同点可能就是都用到了NN(Nears Neighbor)算法，NN的实现一般使用KD（K-dimension tree）树。既然提到了kd树，我们就继续聊聊它吧。

kd树是数据点对k维空间中划分的一种数据结构，主要应用在多维空间数据搜索（如范围搜索和最邻近搜索）。本质上说kd树是一种平衡二叉树。我们以一个例子说明kd树的构建：

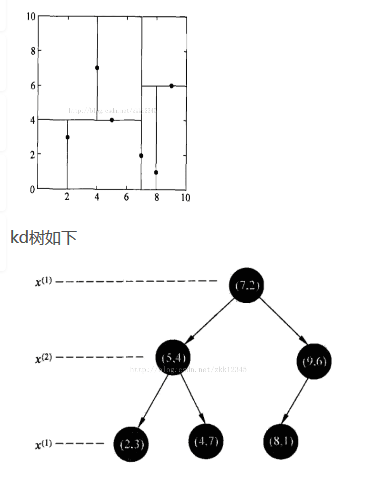
给定一个二维空间的数据集T= {（2,3），（5,4），（9，6），（4,7），（8,1），（7,2）}

首先在k维空间某一特征（这里选择第一个特征说明）-->{2,5,9,4,8,7}，一般取中点来确定超平面（虽然并不是在任何情况下都是最佳），偶数的话选中间靠后的点，即x(1) = 7，然后分成左右两部分{（2,3），（4,7），（5,4）}和{（8,1），（9,6）}；再以第二个特征为准确定超平面，左部分x(2) = 4，以此类推，kd树构建完成：

接着介绍一下在kd树上进行邻近搜索：

比如现在的目标点是（6，1）

1. 通过DFS，在kd树中找到目标点所在的叶节点。

2. 以该叶节点作为当前NN（最邻近）点，计算该节点与目标点之间的距离作为当前的最小距离，这里用欧氏距离。

3. 计算该叶节点父节点到目标点的距离，若小于当前距离，更新最短距离，同时记录之前的NN点。

4. 决定是否进入父节点的另一个子节点：

a) 即第三步的计算结果，如果大，说明没必要继续看其另一边的子树了，以此父节点视为叶节点，重复步骤3。

b) 若小，则进入另一个子节点，重复步骤1，确定另一棵子树中目标点应该在的新叶节点，判断是否更新NN点，接着以此叶节点开始重复步骤3。

以此类推，可以看出整个搜索过程是不断向根节点回退的，回退过程中已经进入过得不再进入。

5. 当退到根节点的时候，此时的NN点即目标点的最邻近点，若求k可以从保存下来的NN点中选择。

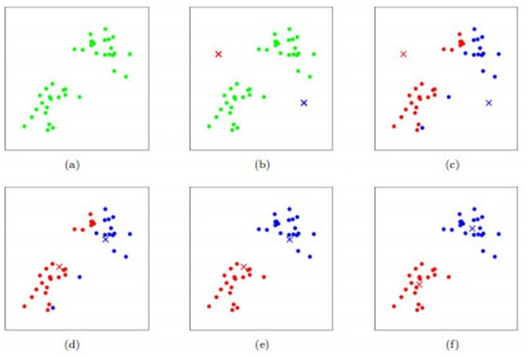
Kmeans算法算是一种非常常见而且使用广泛的聚类算法了。它能把样本对象根据各自属性分成K个聚类，如图所示：

这里K取值为2，Kmeans算法流程就是先初始化k个簇的中心点，根据各点到其距离远近分成K类，接着更新每个簇的中心（即把该簇的所有样本数据坐标相加取平均值），这样不断迭代直至每个簇的中心点不再变化。

Keans因为用到NN，所以也有用到kd树，kmeans把每次更新的簇中心点存成kd树，然后其余的样本点在树中寻找最邻近点确定自己所在的类。

最后总结一下两种算法的异同：

1. KNN是监督的分类算法，Kmeans是无监督的聚类算法。

2. KNN的数据集是带label的，Kmeans则不带。

3. 都有一个给目标点寻找最邻近点的过程，也都用距离相似度来衡量，NN也都用kd树实现。