2013年全国硕士研究生入学统一考试管理类专业学位联考数学试题——纯题目版

2013 级考研管理类联考数学真题

一、问题求解（本大题共 15 小题，每小题 3 分，共 45 分）下列每题给出 5 个选项中，只有一个是符合要求的，请在答题卡上将所选择的字母涂黑。

1.某工厂生产一批零件，计划 10 天完成任务，实际提前 2 天完成任务，则每天的产量比计划平均提高了（ ）.
A.15%
B. 20%
C. 25%
D.30%
E.35%

2.甲乙两人同时从 A 点出发，沿 400 米跑道同向匀速行走，25 分钟后乙比甲少走了一圈， 若乙行走一圈需要 8 分钟，甲的速度是(单位：米/分钟)（ ）.
A.62
B.65
C.66
D.67
E.69

3.甲班共有 30 名学生，在一次满分为 100 分的考试中，全班平均成绩为 90 分，则成绩低于 60 分的学生最多有（ ）人.
A.8
B.7
C.6
D.5
E.4

4.某工程由甲公司承包需要 60 天完成，由甲、乙两公司共同承包需要 28 天完成，由乙、丙两公司共同承包需要 35 天完成，则由丙公司承包完成该工程需要的天数为（ ）天.
A.85
B.90
C.95
D.100
E.105

5.已知$f(x)=\frac{1}{（x+1）（x+2）}+\frac{1}{（x+2）（x+3）}+...+\frac{1}{（x+9）（x+10）}$，则$f(8)=（）$
A.$\frac{1}{9}$
B.$\frac{1}{10}$
C.$\frac{1}{16}$
D.$\frac{1}{17}$
E.$\frac{1}{18}$

6.甲、乙两商店同时购进了一批某品牌电视机，当甲店售出 15 台时，乙店售出 10 台，此时两店的库存比为 8:7，库存差为 5，则甲、乙两店总进货量为（ ）台.
A.85
B.90
C.95
D.100
E.125

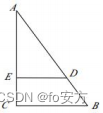
7.如图所示，在直角三角形 ABC 中， AC = 4, BC = 3, DE / /BC .已知梯形 BCED 的面积为 3， 则 DE 的长为（ ）.
A.$\sqrt{3}$
B. $\sqrt{3}+1$
C.$4\sqrt{3}-4$
D.$\frac{3\sqrt{2}}{2}$
E. $\sqrt{3}$

8.点（0,4） 关于直线$2x+y+1=0$的对称点为（ ）.
A.（2,0）
B.（-3,0）
C.（-6,1）
D.（4,2）
E.（-4,2）

9.在$(x^2+3x+1{)}^5$的展开式中, $x^2$的系数为（ ）.
A.5
B.10
C.45
D.90
E.95

10.有一批水果要装箱，一名熟练工单独装箱需要 10 天，每天报酬为 200 元；一名普通工人单独装箱需要 15 天，每天报酬为 120 元，由于场地限制最多同时安排 12 人装箱，若要求在一天内完成装箱任务，则支付的最少报酬为（ ）.
A.1800 元
B.1840 元
C.1920 元
D.1960 元
E.2000 元

11.将体积为$4\pi c{m}^3$和$32\pi c{m}^2$的两个实心金属球熔化后铸成一个实心大球，则大球的表面积为（ ）.
A.$32\pi c{m}^2$
B.$36\pi c{m}^2$
C.$38\pi c{m}^2$
D.$40\pi c{m}^2$
E.$42\pi c{m}^2$

12.已知抛物线$y=x^2+bx+c$的对称轴为 x = 1 ，且过点(-1,1) ，则（ ）.
A. b = -2, c = -2
B. b = 2, c = 2
C. b = -2, c = 2
D. b = -1, c = -1
E. b = 1, c = 1

13.已知{$a_n$}为等差数列，若$a_2$和$a_{10}$是方程$x^2-10x-9=0$的两个根，则$a_5+a_7=$（ ）.
A.-10
B.-9
C.9
D.10
E.12

14.已知 10 件产品中有 4 件一等品，从中任取 2 件，则至少有 1 件一等品的概率为（ ）.
A.$\frac{1}{3}$
B.$\frac{2}{3}$
C.$\frac{2}{15}$
D.$\frac{8}{15}$
E.$\frac{13}{15}$

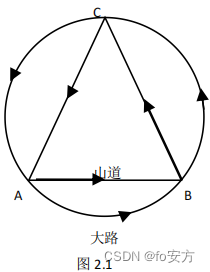
15.确定两人从 A 地出发经过 B，C，沿逆时针方向行走一圈回到 A 地的方案（见图 2），若从 A 地出发时，每人均可选大路或山道，经过 B，C 时至多有 1 人更改道路，则不同的方案有( )
A.16 种
B.24 种
C.36 种
D.48 种
E.64 种

二．条件充分性判断：（第 16-25 小题，每小题 3 分，共 30 分）

要求判断每题给出的条件（1）和（2）能否充分支持题干所陈述的结论，A、B、C、D、E 五个选项为判断结果，请选择一项符合试题要求的判断，请在答题卡上将所选的字母涂黑。
（A）条件（1）充分，但条件（2）不充分
（B）条件（2）充分，但条件（1）不充分
（C）条件（1）和（2）都不充分，但联合起来充分
（D）条件（1）充分，条件（2）也充分
（E）条件（1）不充分，条件（2）也不充分，联合起来仍不充分

16.已知平面区域D1={$(x,y)|x^2+y^2\le 9$}，D2={$(x,y)|(x-x_0{)}^2+(y-y_0{)}^2\le 9$}，则 D1，D2覆盖区域的边界长度为8π.
（1）$x_0^2+y_0^2=9$
（2）$x_0+y_0=3$

17.p = mq + 1为质数.
（1）m 为正整数， q 为质数
（2）m ，q 均为质数

18.△ABC 的边长分别为a, b, c ，则△ABC 为直角三角形.
（1）$(c^2-a^2-b^2)(a^2-b^2)=0$
（2）△ABC 的面积为$\frac{1}{2}ab$

19.已知二次函数$f(x)=a{x}^2+bx+c$，则方程为$f(x)=0$有两个不同实根.
（1）a+c=0
（2）a + b + c = 0

20.档案馆在一个库房安装了n 个烟火感应报警器，每个报警器遇到烟火成功报警的概率为p .该库房遇烟火发出报警的概率达到0.999 .
（1） n = 3, p = 0.9
（2） n = 2, p = 0.97

21.已知a，b 为实数，则$|a|\le 1，|b|\le 1$.
（1）$|a+b|\le 1$
（2）$|a-b|\le 1$

22.设 x, y, z 为非零实数，则$\frac{2x+3y-4z}{-x+y-2z}=1$.
（1） 3x - 2 y = 0
（2） 2 y - z = 0

23.某单位年终奖共发了 100 万元奖金，奖金金额分别是一等奖 1.5 万元、二等奖 1 万元、三等奖 0.5 万元，则该单位至少有 100 人.
（1）得二等奖的人数最多
（2）得三等奖的人数最多

24.三个科室的人数分别为 6、3 和 2，因工作需要，每晚需要排 3 人值班，则在两个月中以便每晚值班人员不完全相同.
（1）值班人员不能来自同一科室
（2）值班人员来自三个不同科室

25.设$a_1=1,a_2=k,...,a_{n+1}=|a_n-a_{n-1}|,(n\ge 2)$ ，则$a_{100}+a_{101}+a_{102}=2$.
（1） k = 2
（2）k 是小于 20 的正整数