codeforces每日5题(均1600)-第三十天

Polycarpus’ Dice

题面翻译

有 $n$ 个骰子，第 $i$ 个骰子朝上的面的可能值在 $1$ 到 $d_i$ 之间，扔了一遍这些骰子之后发现朝上的面的值之和为 $A$

现在需要你对于每一个骰子计算出其抛出多少种值一定凑不成 $A$。$1\le n\le 2\times 10^5$,$n\le A\le \sum d_i$,$1\le d_i\le 10^6$

题目描述

Polycarp has $n$ dice $d_1,d_2,...,d_n$ .

The $i$ -th dice shows numbers from $1$ to $d_i$ .

Polycarp rolled all the dice and the sum of numbers they showed is $A$ .

Agrippina didn’t see which dice showed what number, she knows only the sum $A$ and the values $d_1,d_2,...,d_n$ .

However, she finds it enough to make a series of statements of the following type: dice $i$ couldn’t show number $r$ .

For example, if Polycarp had two six-faced dice and the total sum is $A=11$ , then Agrippina can state that each of the two dice couldn’t show a value less than five (otherwise, the remaining dice must have a value of at least seven, which is impossible).

For each dice find the number of values for which it can be guaranteed that the dice couldn’t show these values if the sum of the shown values is $A$ .

输入格式

The first line contains two integers $n,A$ ( $1<=n<=2\cdot 10^5,n<=A<=s$ ) — the number of dice and the sum of shown values where $s=d_1+d_2+...+d_n$ .

The second line contains $n$ integers $d_1,d_2,...,d_n$ ( $1<=d_i<=10^6$ ), where $d_i$ is the maximum value that the $i$ -th dice can show.

输出格式

Print $n$ integers $b_1,b_2,...,b_n$ , where $b_i$ is the number of values for which it is guaranteed that the $i$ -th dice couldn’t show them.

样例 #1

样例输入 #1

2 8
4 4

样例输出 #1

3 3

样例 #2

样例输入 #2

1 3
5

样例输出 #2

4

样例 #3

样例输入 #3

2 3
2 3

样例输出 #3

0 1

提示

In the first sample from the statement $A$ equal to 8 could be obtained in the only case when both the first and the second dice show 4.

Correspondingly, both dice couldn’t show values 1, 2 or 3.

In the second sample from the statement $A$ equal to 3 could be obtained when the single dice shows 3.

Correspondingly, it couldn’t show 1, 2, 4 or 5.

In the third sample from the statement $A$ equal to 3 could be obtained when one dice shows 1 and the other dice shows 2.

That’s why the first dice doesn’t have any values it couldn’t show and the second dice couldn’t show 3.

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
typedef long long ll;
ll n,a[N],k=0,A;
int main(){cin>>n>>A;for(int i=1;i<=n;i++) scanf("%lld",&a[i]),k+=a[i];for(int i=1;i<=n;i++){ll ans=0;if(A-n+1<a[i]) ans+=(a[i]+n-A-1);if(a[i]+A-k-1>=0) ans+=(A-k+a[i]-1);printf("%lld ",ans); }return 0;
}

Ilya and Sticks

题面翻译

给定 $n$ 根木棍的长度 $f[i]$ ，木棍长度可以根据需要，削减 $1$ 个单位，现在要在 $n$ 根木棍中选出一些木棍，拼成若干个长方形，求最大面积和。

题目描述

In the evening, after the contest Ilya was bored, and he really felt like maximizing.

He remembered that he had a set of $n$ sticks and an instrument.

Each stick is characterized by its length $l_i$ .

Ilya decided to make a rectangle from the sticks.

And due to his whim, he decided to make rectangles in such a way that maximizes their total area.

Each stick is used in making at most one rectangle, it is possible that some of sticks remain unused.

Bending sticks is not allowed.

Sticks with lengths $a_1$ , $a_2$ , $a_3$ and $a_4$ can make a rectangle if the following properties are observed:

• $a_1<=a_2<=a_3<=a_4$
• $a_1=a_2$
• $a_3=a_4$

A rectangle can be made of sticks with lengths of, for example, $3333$ or $2244$ .

A rectangle cannot be made of, for example, sticks $5557$ .

Ilya also has an instrument which can reduce the length of the sticks.

The sticks are made of a special material, so the length of each stick can be reduced by at most one.

For example, a stick with length $5$ can either stay at this length or be transformed into a stick of length $4$ .

You have to answer the question — what maximum total area of the rectangles can Ilya get with a file if makes rectangles from the available sticks?

输入格式

The first line of the input contains a positive integer $n$ ( $1<=n<=10^5$ ) — the number of the available sticks.

The second line of the input contains $n$ positive integers $l_i$ ( $2<=l_i<=10^6$ ) — the lengths of the sticks.

输出格式

The first line of the output must contain a single non-negative integer — the maximum total area of the rectangles that Ilya can make from the available sticks.

样例 #1

样例输入 #1

4
2 4 4 2

样例输出 #1

8

样例 #2

样例输入 #2

4
2 2 3 5

样例输出 #2

0

样例 #3

样例输入 #3

4
100003 100004 100005 100006

样例输出 #3

10000800015

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
typedef long long ll;
ll n,a[N],k;
ll ans=0;
int main(){cin>>n;for(int i=1;i<=n;i++) scanf("%lld",&a[i]);sort(a+1,a+1+n);for(int i=n-1;i>=1;i--){if(a[i+1]-a[i]<2){if(k) ans+=k*a[i],k=0;else k=a[i];i--;}}cout<<ans;return 0;
}

Gerald’s Hexagon

题面翻译

按顺时针顺序给出一个六个内角全部都是120°的六边形六条边的边长,求该六边形剖分成三条边边长全部为$1$的等边三角形的个数.
保证该六边形能够剖分成若干个边长全部为$1$的等边三角形.

题目描述

Gerald got a very curious hexagon for his birthday.

The boy found out that all the angles of the hexagon are equal to . Then he measured the length of its sides, and found that each of them is equal to an integer number of centimeters.

There the properties of the hexagon ended and Gerald decided to draw on it.

He painted a few lines, parallel to the sides of the hexagon.

The lines split the hexagon into regular triangles with sides of 1 centimeter.

Now Gerald wonders how many triangles he has got.

But there were so many of them that Gerald lost the track of his counting.

Help the boy count the triangles.

输入格式

The first and the single line of the input contains 6 space-separated integers $a_1,a_2,a_3,a_4,a_5$ and $a_6$ ( $1<=a_i<=1000$ ) — the lengths of the sides of the hexagons in centimeters in the clockwise order.

It is guaranteed that the hexagon with the indicated properties and the exactly such sides exists.

输出格式

Print a single integer — the number of triangles with the sides of one 1 centimeter, into which the hexagon is split.

样例 #1

样例输入 #1

1 1 1 1 1 1

样例输出 #1

6

样例 #2

样例输入 #2

1 2 1 2 1 2

样例输出 #2

13

提示

This is what Gerald’s hexagon looks like in the first sample:

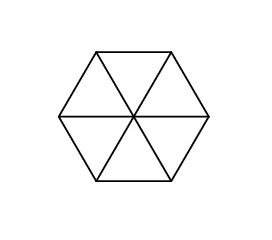
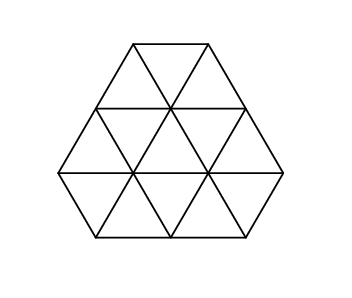
And that’s what it looks like in the second sample:

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
typedef long long ll;
int a,b,c,d,e,f;
int main(){cin>>a>>b>>c>>d>>e>>f;cout<<(a+b+c)*(a+b+c)-a*a-c*c-e*e;return 0;
}

Statistics of Recompressing Videos

题面翻译

有一个网站叫DH，有 $n$ 个视频和 $k$ 个服务器。每个服务器可以同时压缩一个视频。

多个服务器可以一起工作。

现在给定每个视频的长度 $m_i$ 和两两不等的上传时间 $s_i$（每个视频只有在上传了之后才可以压缩）输出每个视频开始压缩的时间，使得总时间最短。以 $s_i$ 单调上升给出。

题目描述

A social network for dogs called DH (DogHouse) has $k$ special servers to recompress uploaded videos of cute cats.

After each video is uploaded, it should be recompressed on one (any) of the servers, and only after that it can be saved in the social network.

We know that each server takes one second to recompress a one minute fragment.

Thus, any server takes $m$ seconds to recompress a $m$ minute video.

We know the time when each of the $n$ videos were uploaded to the network (in seconds starting from the moment all servers started working).

All videos appear at different moments of time and they are recompressed in the order they appear.

If some video appeared at time $s$ , then its recompressing can start at that very moment, immediately.

Some videos can await recompressing when all the servers are busy.

In this case, as soon as a server is available, it immediately starts recompressing another video.

The videos that await recompressing go in a queue.

If by the moment the videos started being recompressed some servers are available, then any of them starts recompressing the video.

For each video find the moment it stops being recompressed.

输入格式

The first line of the input contains integers $n$ and $k$ ( $1<=n,k<=5\cdot 10^5$ ) — the number of videos and servers, respectively.

Next $n$ lines contain the descriptions of the videos as pairs of integers $s_i,m_i$ ( $1<=s_i,m_i<=10^9$ ), where $s_i$ is the time in seconds when the $i$ -th video appeared and $m_i$ is its duration in minutes.

It is guaranteed that all the $s_i$ 's are distinct and the videos are given in the chronological order of upload, that is in the order of increasing $s_i$ .

输出格式

Print $n$ numbers $e_1,e_2,...,e_n$ , where $e_i$ is the time in seconds after the servers start working, when the $i$ -th video will be recompressed.

样例 #1

样例输入 #1

3 2
1 5
2 5
3 5

样例输出 #1

6
7
11

样例 #2

样例输入 #2

6 1
1 1000000000
2 1000000000
3 1000000000
4 1000000000
5 1000000000
6 3

样例输出 #2

1000000001
2000000001
3000000001
4000000001
5000000001
5000000004

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
typedef long long ll;
ll n,k,s,m;
priority_queue<long long,vector<long long>,greater<long long> >q; 
int main(){cin>>n>>k;for(int i=1;i<=n;i++){scanf("%lld%lld",&s,&m);if(q.size()>=k){s=max(s,q.top())+m;q.pop();}else s+=m;q.push(s);printf("%lld\n",s);}return 0;
}

Anya and Smartphone

题面翻译

题目描述

安雅购买了一只带有Berdroid操作系统的智能手机

智能手机菜单中有n个应用，每个应用程序都有其自己的图标

每个应用的图标都在相应的屏幕上，一个屏幕包含ķ个图标

第1个应用到第k个应用的图标位于第一个屏幕上，从第（k + 1）个至第2k个应用在第二个屏幕上，依次类推（最后屏幕可以是部分为空） 。

开始的时候，智能手机显示的屏幕是第一个屏幕，为了去启动第t个屏幕上的应用，安雅需要做如下的手势：首先是连续切换屏幕t-1次，其次是点击第t个屏幕上的那个应用程序。

在应用程序启动以后，屏幕会重新返回到第1个屏幕

也就是说，如果你要启动下一个程序，必须又要重头来过。

所有应用程序的编号是从1到n

我们知道所有屏幕中每个应用程序的位置。但是Berdroid是智能系统，他会根据用户实际的使用情况，自动把使用次数最多的应用放到最前面

变化规则是这样的，当一个应用程序启动以后，系统会自动的将该程序的图标位置和他前面的那个应用程序的图标互换位置（可能会导致图标不在原来的屏幕上）

当然了，如果那个被启动的应用程序已经在第一个位置上了，就不需要再更换位置了。

如果你已经知道安雅启动某些应用程序的顺序，请你来计算他需要多个手势（切换一个屏幕或者点击一个应用程序图标都算作一次手势）来完成这些任务。

注意，一个应用可以发起多次。

输入格式：
输入的第一行包含三个整数n，m，k（1≤n，m，k≤10^5),n表示应用程序的数量，m表示将要启动的应用程序的数量，k表示每个屏幕上图标的数量。

第二行包含n个整数，分别为a1，a2，…，an，表示初始的时候应用程序图标的顺序，按照这个顺序放到一个个屏幕中去。ai是每个应用程序的编号，ai不会重复。

第三行包含m个整数b1，b2，…，bm（1≤bm≤n），表示安雅计划启动的应用程序的编号。一个应用程序可能会启动多次。

输出格式

输出一个整数，表示安雅完成这些任务需要使用的手势次数。

输入样例1：
8 3 3
1 2 3 4 5 6 7 8
7 8 1

输入样例2：
5 4 2
3 1 5 2 4
4 4 4 4

输出样例1：
7

输出样例2：
8

提示

在第一个样例中的起始位置是（123）（456）（78），也就是，在第一个屏幕包含应用程序1，2，3的图标，第二个屏幕包含图标4，5，6，第三个屏幕包含图标7,8。

应用7启动后，我们得到新的图标位置-（123）（457）（68）。这过程需要3次手势。

应用8被启动后，我们得到的位置（123）（457）（86），要启动它安雅需要使用3次手势。

应用1启动后，图标菜单中的排列没有变化，要启动它安雅需要1次手势。

所以说，总共需要3+3+1=7次手势。

题目描述

Anya has bought a new smartphone that uses Berdroid operating system.

The smartphone menu has exactly $n$ applications, each application has its own icon.

The icons are located on different screens, one screen contains $k$ icons. The icons from the first to the $k$ -th one are located on the first screen, from the $(k+1)$ -th to the $2k$ -th ones are on the second screen and so on (the last screen may be partially empty).

Initially the smartphone menu is showing the screen number $1$ .

To launch the application with the icon located on the screen $t$ , Anya needs to make the following gestures: first she scrolls to the required screen number $t$ , by making $t-1$ gestures (if the icon is on the screen $t$ ), and then make another gesture — press the icon of the required application exactly once to launch it.

After the application is launched, the menu returns to the first screen.

That is, to launch the next application you need to scroll through the menu again starting from the screen number $1$ .

All applications are numbered from $1$ to $n$ .

We know a certain order in which the icons of the applications are located in the menu at the beginning, but it changes as long as you use the operating system.

Berdroid is intelligent system, so it changes the order of the icons by moving the more frequently used icons to the beginning of the list.

Formally, right after an application is launched, Berdroid swaps the application icon and the icon of a preceding application (that is, the icon of an application on the position that is smaller by one in the order of menu).

The preceding icon may possibly be located on the adjacent screen.

The only exception is when the icon of the launched application already occupies the first place, in this case the icon arrangement doesn’t change.

Anya has planned the order in which she will launch applications.

How many gestures should Anya make to launch the applications in the planned order?

Note that one application may be launched multiple times.

输入格式

The first line of the input contains three numbers $n,m,k$ ( $1<=n,m,k<=10^5$ ) — the number of applications that Anya has on her smartphone, the number of applications that will be launched and the number of icons that are located on the same screen.

The next line contains $n$ integers, permutation $a_1,a_2,...,a_n$ — the initial order of icons from left to right in the menu (from the first to the last one), $a_i$ — is the id of the application, whose icon goes $i$ -th in the menu.

Each integer from $1$ to $n$ occurs exactly once among $a_i$ .

The third line contains $m$ integers $b_1,b_2,...,b_m(1<=b_i<=n)$ — the ids of the launched applications in the planned order.

One application may be launched multiple times.

输出格式

Print a single number — the number of gestures that Anya needs to make to launch all the applications in the desired order.

样例 #1

样例输入 #1

8 3 3
1 2 3 4 5 6 7 8
7 8 1

样例输出 #1

7

样例 #2

样例输入 #2

5 4 2
3 1 5 2 4
4 4 4 4

样例输出 #2

8

提示

In the first test the initial configuration looks like $(123)(456)(78)$ , that is, the first screen contains icons of applications $1,2,3$ , the second screen contains icons $4,5,6$ , the third screen contains icons $7,8$ .

After application $7$ is launched, we get the new arrangement of the icons — $(123)(457)(68)$ .

To launch it Anya makes $3$ gestures.

After application $8$ is launched, we get configuration $(123)(457)(86)$ .

To launch it Anya makes $3$ gestures.

After application $1$ is launched, the arrangement of icons in the menu doesn’t change.

To launch it Anya makes $1$ gesture.

In total, Anya makes $7$ gestures.

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
typedef long long ll;
int n,m,k,a[N],id[N],b,pos,temp;
long long ans;
int main(){cin>>n>>m>>k;for(int i=1;i<=n;i++){scanf("%d",&a[i]);id[a[i]]=i;}while(m--){scanf("%d",&b);pos=id[b];ans+=(pos-1)/k+1;if(pos==1) continue;--id[a[pos]];++id[a[pos-1]];swap(a[pos],a[pos-1]);}cout<<ans;return 0;
}