描述
xiaomengxian一进门,发现外公、外婆、叔叔、阿姨……都坐在客厅里等着他呢。经过仔细观察,xiaomengxian发现他们所有人正好组成了一个凸多边形。最重要的是,他们每个人手里都拿着一个红包(^o^)。于是非常心急,xiaomengxian决定找一条最短的路线,拿到所有的红包。
假设屋里共有N个人拿着红包,把他们分别从1到N编号。其中,编号为1的人就坐在大门口,xiaomengxian必须从这里出发去拿其它的红包。一条合法的路线必须经过所有的点一次且仅一次。
格式
输入格式
第一行为一个整数N(1<=N<=800)。
以下N行,每行两个实数Xi,Yi,表示该点的坐标。
各个点按照逆时针顺序依次给出。
输出格式
一个实数,表示最短的路线长度(保留三位小数)。
样例1
样例输入1
4
50.0 1.0
5.0 1.0
0.0 0.0
45.0 0.0样例输出1
50.211限制
各个测试点1s
来源
Xiaomengxian


1 #include <iostream> 2 #include <algorithm> 3 #include <cstdio> 4 #include <stdlib.h> 5 #include <math.h> 6 7 using namespace std; 8 9 const int maxn=1000; 10 int n; 11 double dis[maxn][maxn]; 12 13 struct node{ 14 double x,y; 15 }p[maxn]; 16 17 double f[maxn][maxn][2];//编号;经过几个点;分两个数组分别存放由第一个点到第二个点(遍历之间的所有点)的最短路径和第二个点到第一个点的最短路径 18 19 void init(){ 20 scanf("%d",&n); 21 for(int i=0;i<=n-1;i++) 22 scanf("%lf%lf",&p[i].x,&p[i].y); 23 } 24 double distan(node a,node b){ 25 return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)); 26 } 27 28 int main() 29 { 30 double ans=99999999; 31 init(); 32 for(int i=0;i<=n-1;i++) 33 for(int j=0;j<=n-1;j++){ 34 dis[i][j]=distan(p[i],p[j]); 35 } 36 for(int i=2;i<=n;i++) 37 for(int j=0;j<=n-1;j++){ 38 f[j][i][1]=min(f[j][i-1][0]+dis[j][(j+i-1)%n],f[j][i-1][1]+dis[(j+i-1)%n][j]); 39 f[j][i][0]=min(f[(j+1)%n][i-1][0]+dis[j][(j+1)%n],f[(j+1)%n][i-1][1]+dis[j][(j+i-1)%n]); 40 } 41 for(int i=0;i<=n-1;i++) 42 ans=min(f[i][n][0],ans); 43 printf("%.3lf\n",ans); 44 return 0; 45 }
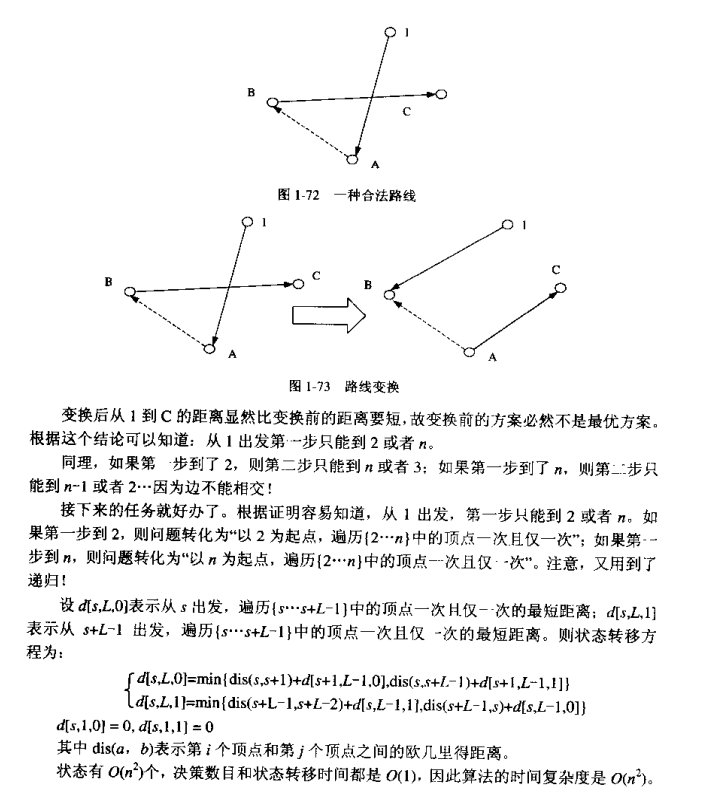
前提:最短Hamilton链中不存在相交的边。
首先要明确一下模糊的题意:其实就是哈密顿回路少掉一条边,所有的点都可能是出发点,而不是数据里的第一个点出发
设f(s,l,0)为从s遍历l个点(s....s+l-1)的最短距离,f(s,l,1)为从s+l-1遍历l个点(s+l-1...s)的最短距离
其实就是把从s遍历l个点分为两步:
1.从s出发,由于轨迹不能有相交,所以下一步只能是去左边或右边两个相邻点s1和s2(详细证明见附录)
2.从s1到s2遍历/s2到s1遍历(不是开头结尾就是s1 s2的意思,而是把这些所有的点都遍历到)
附录:
下面是算法艺术与信息学竞赛p133-134页和本题几乎一样的例题和解释,比较清楚,贴上来