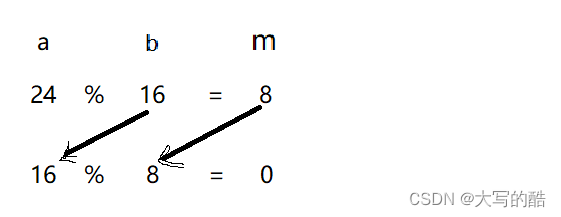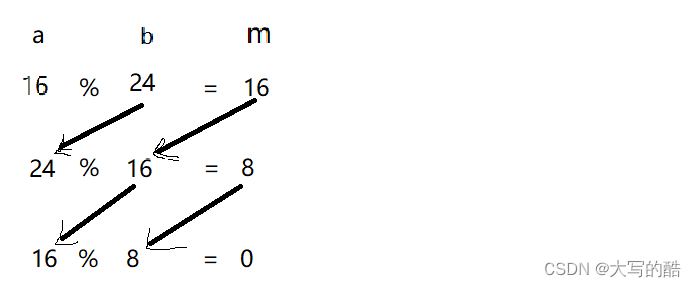yo！这里是常见问题的特殊（大佬）解法-总结

目录

前言

常见问题

最大公约数

1.问题介绍

2.解决方法

不创建临时变量交换两个变量的值

1.问题介绍

2.解决方法

求二进制中1的个数

1.问题介绍

2.解决方法

左旋字符串

1.问题介绍

2.解决方法

 更新中......

前言

       在一些常见的笔试面试的题目求解方法中，除了比较容易想到（暴力）的方法之外，还有非常不容易想到的方法，那这些方法呢，在一些中小厂笔试或面试环节（大厂大部分都是原创题）过程中，面试官会想要听到。比如，问你一个问题之后，你可能就问题阐述了一个直接想得到的方法，但是面试官下一步就会问你有无更加优化的方法，那么此时你可以通过在此文的学习后能够回答出面试官的进一步加问，让面试官眼前一亮。

       这是一个长期积累的过程，我也只是整理了一部分，在后续的学习中，我会更新更多，那么大家也可以在评论区讨论甚至更优的方法以及其他问题的特殊方法，我看到也会整理到文章其中，供大家参考学习与交流。

       希望大家不要只看一遍就觉得自己会了，也不是死记硬背，而一定要去反复的理解思路过程，周期性的回来复习一下，那么久而久之，量变就会引起质变。加油！

常见问题

• 最大公约数

1.问题介绍

       求出两个数的最大公约数，如果有一个自然数a能被自然数b整除，则称a为b的倍数，b为a的约数。几个自然数公有的约数，叫做这几个自然数的公约数。公约数中最大的一个公约数，称为这几个自然数的最大公约数。

2.解决方法

       这里不再介绍穷举法等比较暴力的方法，说一下辗转相除法

思路过程：

       需求最大公约数的两个数赋给a、b，将a%b赋给m，之后，将b赋给a，m赋给b，再a%b赋给m，循环直到m为0，此时最大公约数为b的值。比如，

        代码：

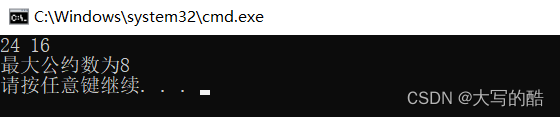
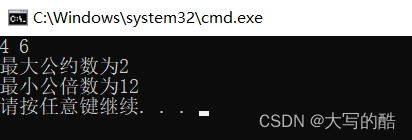
int main()
{int a = 0,b = 0,m = 0;scanf("%d %d",&a,&b);m = a%b;while (m){a = b;b = m;m = a%b;}printf("最大公约数为%d\n",b);return 0;
}

 测试：

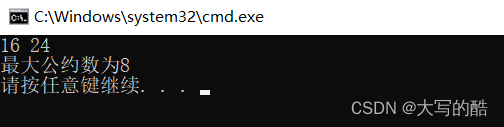
ps：有老铁可能会说a%b的话，一定要a放较大数，b放较小数，其实并不需要，看图

       这里提一嘴最小公倍数，在算出最大公约数之后，最小公倍数就是最初的a乘以b除以最大公约数，代码：

//_a和_b为最初的需求最大公约数的两个数，b为最大公约数
printf("最小公倍数为%d\n",_a*_b/b);

测试：

• 不创建临时变量交换两个变量的值

1.问题介绍

       “交换两个变量的值？？？就这！有手就行，看我随随便便int tmp=x;x=y;y=tmp; 啊......不创建临时变量。”这应该是每个小白的内心戏了吧哈哈，对没看错，不能创建临时变量交换两个变量的值。

2.解决方法

       不创建临时变量交换两个变量的值，其实方法也有很多，在这里介绍一下异或法吧，先说一下什么是异或，异或是按位异或，是一种操作符，位指的是二进制数，口诀：相同为0，不同为1。

思路过程：

       1.异或的特点：有任意数，

①a^0=0;   

②a^a=0;   

③满足交换律，

根据这些特点，大家去看这样一个例子：1^2^3^2^1=1^1^2^2^3=3，有没有感觉对异或有了一个新的认知呢。

       2.见下方代码，核心部分为①x = x^y;   ②y = x^y;   ③x = x^y; ，

经①，x中存放的是x^y，此时②就变成了y=x^y^y，

经②，y中存放的是原先的x，x中依旧是x^y，此时③就变成了x=x^y^x，

经③，x的值是是原先的y，

所以，经过核心部分，x、y的值就发生了交换。

代码：

int main()
{int x = 3;int y = 5;printf("交换前：\n");printf("%d %d\n",x,y);x = x^y;y = x^y;x = x^y;printf("交换后：\n");printf("%d %d\n", x, y);return 0;
}

测试：

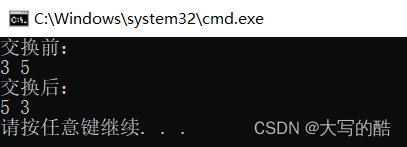
 ps：异或法很巧妙，但存在缺点，就是只能交换两个整数的值，因为异或只能作用于整数，所以建议遇到需要交换两个变量的值时，还是使用临时变量的方法，即简单又快捷又不挑作用数据类型。

• 求二进制中1的个数

1.问题介绍

       求二进制中1的个数，这是对于整数而言的，因为我们知道整数在计算机中是以补码的形式存在的，这里就是说，给定一个整数，需给出这个整数的补码的二进制中1的个数，比如，

①整数3，补码的二进制：000000000000000000000000 0000 0011，1的个数为2；

②整数13，补码的二进制：0000000000000000000000 0000 1101，1的个数为1；

③整数-1，补码的二进制：11111111111111111111111111111111，1的个数为32，

所以，我们就要用程序来实现这样的一个功能。

2.解决方法

       第一种方法，是大家相对容易想到的方法，就是利用按位右移符>>及按位与&的特点。

思路过程：

       在学习过按位与和按位或的知识点之后，容易了解到：

①一个二进制数 & 1 之后不变，& 0之后变0；

②一个二进制数 | 0之后不变，| 1之后变1，

所以给我们一个数，将其 & 1之后，就能得到这个数的二进制形式的最后一位数字，再按位右移>>1，再 & 1循环往复32次，就能得到二进制中1的个数。

例如：

整数5（补码为000000000000000000000000 0000 0101），

①按位与1（补码为000000000000000000000000 0000 0001），得到补码000000000000000000000000 0000 0001，即整数1，得到二进制的最后一位是1，

此时，将5>>1,得到补码000000000000000000000000 0000 0010，

②再按位与1，得到补码000000000000000000000000 0000 0000，即整数0，得到二进制倒数第二位为0，

③循环32次，就得到二进制数的每一位，同时用计数器count统计其中1的个数，得解。

代码：

int _1NumberOf1(int n) {int i = 0;int count = 0;while (i < 32){i++;if ((n & 1) == 1){count++;}n >>= 1;}return count;
}

       第二种方法，就是类比 “求得一个十进制整数的每一位数字” 这个问题的思路，当我们需要求得二进制整数的每一位数字，是不是也可以用相同的办法？

思路过程：

       我们先来看问题“求得一个十进制整数的每一位数字”，方法是，先%10，再 /10，循环直到这个数为0停止，期间通过输出%10之后的数字就是十进制整数的每一位数字，那类比到二进制整数，是不是也可以得到二进制整数的每一位数字呢，答案是可以的。

代码：

int _2NumberOf1(int n)
{int count = 0;unsigned int m = n;while (m){if (m % 2 == 1)count++;m /= 2;}return count;
}

       第三种方法，相对于上面两种方法是非常难以想到的方法，也呼应了笔者写这篇文章的初衷。

思路过程：

       借助n=n&(n-1)的巧妙之处，举个栗子：

整数n为13，二进制为1101，此时n-1的二进制为1100，

①按位与之后得到1100再赋给n，此时n-1为1011，

②按位与之后得到1000赋给n，此时n-1为0111，

③按位与之后得到0000赋给n，

我们可以看到n为0之前进行了三次按位与，而且原始的n的二进制中1的个数就是3，这是巧合吗，no，是巧妙，举多个栗子之后就会发现n=n&(n-1)的执行次数就是n的二进制中1的个数。

代码：

int _3NumberOf1(int n)
{int count = 0;while (n){n = n & (n - 1);count++;}return count;
}

三种方法的测试：

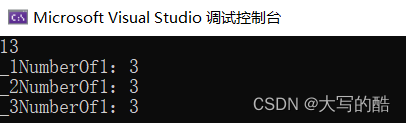
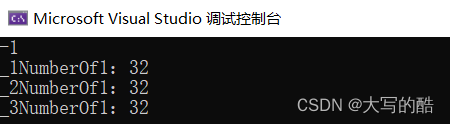
• 左旋字符串

1.问题介绍

        左旋字符串，顾名思义，向左旋转字符串的k个字符位，比如，字符串位"abcdef"，要求左旋四个字符位，即"efabcd"，左旋8个字符位，即"cdefab"。

2.解决方法

        小伙伴们看到这个题目，应该会想到这种方法：保存第一个字符，将后面的所有字符向前移，循环k次即可，我想大家按照这个思路写出程序不是问题，但是我想介绍一种借助反转字符串的方法。

思路过程：

       反转字符串：将字符串颠倒存放，比如，字符串"abcd"，反转之后变成"dcba"，现要求左旋字符串的k个字符位，

①反转前k个字符组成的字符串；

②反转剩下的字符组成的字符串；

③反转整个字符串，

比如，有字符串"abcdef"，左旋2个字符位，

①"ab"--->"ba"；

②"cdef"--->"fedc"；

③"bafedc"--->"cdefab"，得解

代码：

//反转字符串
void reverse_str(char* left, char* right)
{while (left < right){char tmp = *left;*left = *right;*right = tmp;left++;right--;}
}
//左旋字符串
void LeftRotate_k2(char arr[], int k)
{int sz = strlen(arr);k %= sz;reverse_str(arr, arr + k - 1);reverse_str(arr + k, arr + sz - 1);reverse_str(arr, arr + sz - 1);
}
//ps：k%=sz;，是因为对于一个字符串，比如长度为4，左旋10个字符位就相当于左旋2个字符位

测试：

 更新中......