1115 Counting Nodes in a Binary Search Tree（30分）

本文主要是介绍1115 Counting Nodes in a Binary Search Tree（30分），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目翻译：

给定一组序列，请建立二叉搜索树

题解思路：

注意是二叉搜索树BST，而非平衡二叉树AVL，两者的区别如下：

BST：

AVL：

因此只需要采用常规的建树手段即可，需要注意的是什么时候采用指针，什么时候不采用指针类型更好：

对于类似这种左右子树的值都已给出的话采用非指针建树更好（用一个结构体数组来存储）

而对于给定一串序列让你建立这个树（没有点明左右孩子关系的话），采用指针类型结构体更好：

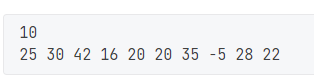
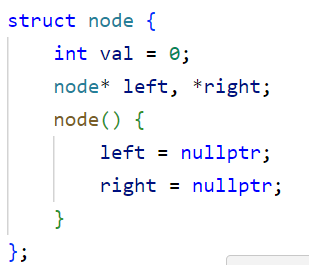
代码：

#include<bits/stdc++.h>
using namespace std;
int N;
vector<int> lev[1001];struct node {int val = 0;node* left, *right;node() {left = nullptr;right = nullptr;}
};node* insert(node* root, int num, int curlev)
{if (root == nullptr){root = new node();root->val = num;lev[curlev].push_back(num);return root;}if (num <= root->val)root->left = insert(root->left, num, curlev + 1);elseroot->right = insert(root->right, num, curlev + 1);return root;
}int main()
{int temp;cin >> N ;node* root = nullptr;for (int i = 0;i < N;i++){cin >> temp;root = insert(root, temp, 0);}int result = 0;while (lev[result].size())result++;if (result == 1)cout << lev[result - 1].size() << " + " << 0 << " = " << lev[result - 1].size();elsecout << lev[result - 1].size() << " + " << lev[result - 2].size() << " = " << lev[result - 2].size() + lev[result - 1].size();
}