本文主要是介绍格密码学习笔记(二):连续极小、覆盖半径和平滑参数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 最短距离和连续极小值
- 距离函数和覆盖半径
- 格的平滑参数
- 致谢
最短距离和连续极小值
除了行列式,格的另一个基本量是格上最短非零向量的长度,即格中最短距离,其定义为
λ 1 = min x , y ∈ L , x ≠ y ∥ x − y ∥ = min z ∈ L , z ≠ 0 ∥ z ∥ . \begin{aligned} \lambda_1 &= \min_{\bm{x,y} \in \mathcal{L}, \bm{x} \neq \bm{y}} \| \bm{x} - \bm{y} \| \\ &= \min_{\bm{z} \in \mathcal{L}, \bm{z} \neq \bm{0}} \| \bm{z} \|. \end{aligned} λ1=x,y∈L,x=ymin∥x−y∥=z∈L,z=0min∥z∥.
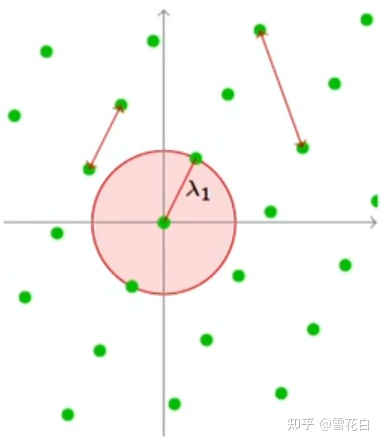
如上图所示,两两格点构成的向量都可以通过平移得到起始点为原点的向量,通过找到距离原点最近的格点即可计算出格中最短距离。格中最短距离也称为第一连续极小,记为 λ 1 \lambda_1 λ1。
同理可定义第二至第 n n n连续极小 λ 2 , … , λ n \lambda_2, \dots, \lambda_n λ2,…,λn。
在二维格上,可以用多项式时间算法求解出 λ 1 \lambda_1 λ1,但在多维格上求解 λ 1 \lambda_1 λ1则十分困难。注意,给定一组格基,最短向量不一定是格基之一。
定义1 在格 L \mathcal{L} L中,第 i i i连续极小值( i = 1 , … , n i=1,\dots, n i=1,…,n) 为 λ i = min { r : d i m s p a n ( B ( r ) ∩ L ) ≥ i } \lambda_i = \min \{ r : \mathrm{dim} ~ \mathrm{span}(\mathcal{B}(r) \cap \mathcal{L}) \geq i \} λi=min{r:dim span(B(r)∩L)≥i}。
在定义1中, B ( r ) \mathcal{B}(r) B(r)表示半径为 r r r的超球体(Ball),该超球体与格 L \mathcal{L} L交集产生的向量张成( s p a n \mathrm{span} span)的空间的维度( d i m \mathrm{dim} dim)为 i i i。换而言之,第 i i i连续极小值即包含至少 i i i个线性无关格向量的最小球的半径。
把球的中心放在原点,若球中有非零格向量,那么球中不止一个格向量。以上图为例,红色区域包含了一个非零格向量以及它的逆向量,但这二者在同一条直线上,仅张成一维空间,该超球体的半径是 λ 1 \lambda_1 λ1。而以下图为例,一个更大的超球体包含了4个非零格向量,可以张成二维空间,该超球体的半径是 λ 2 \lambda_2 λ2。

在整数格 Z n \mathbb{Z}^n Zn中,有 λ 1 = λ 2 = ⋯ = λ n \lambda_1 = \lambda_2 = \cdots = \lambda_n λ1=λ2=⋯=λn。一般而言, λ 1 ≤ λ 2 ⋯ ≤ λ n \lambda_1 \leq \lambda_2 \cdots \leq \lambda_n λ1≤λ2⋯≤λn。
距离函数和覆盖半径
对任意点 t ∈ R n \bm{t} \in \mathbb{R}^n t∈Rn,记距离函数 μ ( t , L ) \mu(\bm{t}, \mathcal{L}) μ(t,L)返回 t \bm{t} t到最近格点的距离,即 μ ( x , L ) = min x ∈ L ∥ t − x ∥ \mu(\bm{x}, \mathcal{L}) = \min_{\bm{x} \in \mathcal{L}} \| \bm{t} - \bm{x} \| μ(x,L)=minx∈L∥t−x∥。
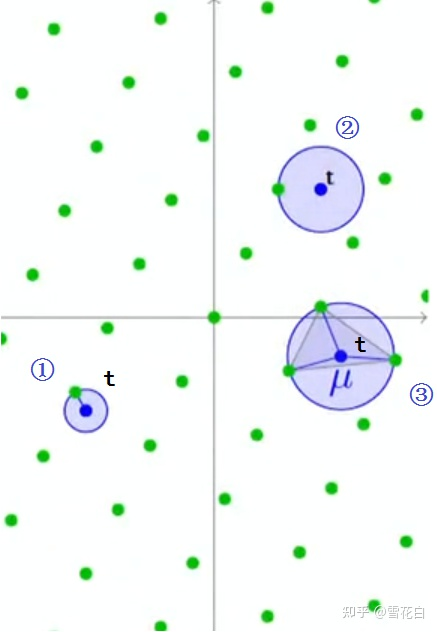
通过移动 t \bm{t} t可以找到 μ \mu μ的最大值,称为覆盖半径,即 μ ( L ) = max t ∈ s p a n ( L ) μ ( t , L ) \mu(\mathcal{L}) = \max_{\bm{t} \in \mathrm{span}(\mathcal{L})} \mu(\bm{t}, \mathcal{L}) μ(L)=maxt∈span(L)μ(t,L)。以下图为例, t \bm{t} t从①移动至②再移动至③,此时无论 t \bm{t} t再怎么移动都会减小 μ \mu μ的值,故 μ \mu μ在步骤③时达到最大。
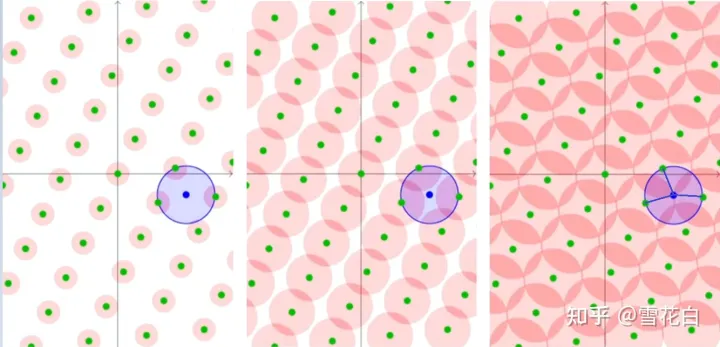
以下图为例,将所有格点作为球心,不断增大球的半径 r r r,当半径 r r r超过 1 2 λ 1 \frac{1}{2} \lambda_1 21λ1时这些球开始互相覆盖,而当空间中所有点都被这些球覆盖时 r r r刚好等于 μ \mu μ的最大值,名称“覆盖半径”由此而来。想象一下,在下图的第三张子图里,若再移动蓝色点 t \bm{t} t均会落在球的内部从而使 μ \mu μ变小。
格的平滑参数
假设噪声 γ \bm{\gamma} γ随机采样自均匀分布 U ( [ 0 , r ] n ) \mathrm{U}([0, r]^n) U([0,r]n),记格点为 x ∈ L \bm{x} \in \mathcal{L} x∈L,为使 γ + x \bm{\gamma} + \bm{x} γ+x的分布看起来与 U ( R n ) \mathrm{U}(\mathbb{R}^n) U(Rn)无异,要使 r r r足够大。以上图为例, γ + x \bm{\gamma} + \bm{x} γ+x的出现频数用红色深浅表示,当 r r r太小时有些地方是空白色,随着 r r r的增大有些区域红色的深浅程度不一,当 r r r无穷大时所有区域颜色一样。
当 r r r是无穷大时是最理想的状态。事实上,存在一个有限的 r ^ \hat{r} r^值可使 γ + x \bm{\gamma} + \bm{x} γ+x趋近于完全均匀分布,有 max μ ≤ ∥ r ^ ∥ ≤ log ( n ) ⋅ n λ n \max \mu \leq \| \hat{r} \| \leq \log(n) \cdot \sqrt{n} \lambda_n maxμ≤∥r^∥≤log(n)⋅nλn。
注:下面笔记属于个人猜测,高斯噪声这块公开课讲得比较模糊,强烈建议查阅原始论文。
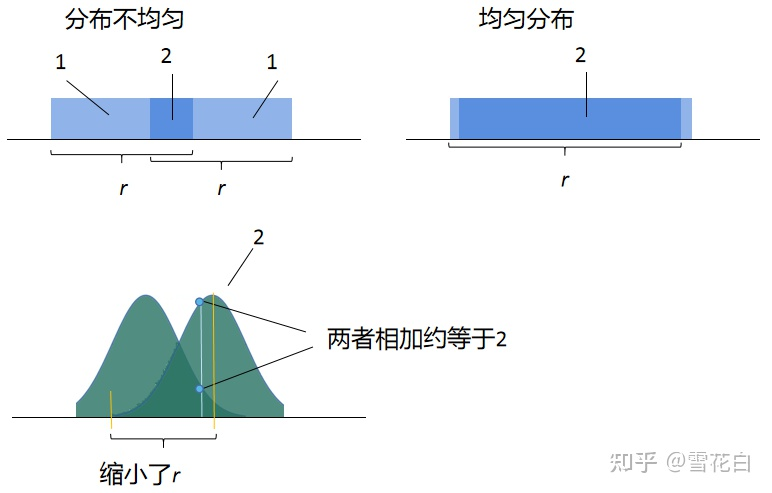
球的半径要取得很大是因为它的边界十分明显。为解决该问题,可以使球心到边界逐渐平滑,即采用球状高斯分布进行平滑,从而得到高斯噪声。以下图为例,高斯平滑缩小了 r r r值。对半径对应向量的每个分量 v i \bm{v}_i vi,应使得 ∥ v i ∥ ≈ η ϵ ≤ log ( n ) λ n \| \bm{v}_i \| \approx \eta_\epsilon \leq \log(n) \lambda_n ∥vi∥≈ηϵ≤log(n)λn,仅略大于 λ n \lambda_n λn,此处 η ϵ \eta_\epsilon ηϵ被称为平滑参数。一般而言, η ϵ \eta_\epsilon ηϵ由一个错误参数 ϵ \epsilon ϵ决定, ϵ \epsilon ϵ表示当前噪声分布和均匀噪声分布之间的差异。
致谢
- Simons格密码公开课官网
Mathematics of Lattices - Simons Institute for the Theory of Computing
- 哔哩哔哩中英双语视频(字幕组:重庆大学大数据与软件学院 后量子密码研究小组)
【中英字幕】Simons格密码讲座第1讲:格的数学定义_哔哩哔哩_bilibili
- 其它格密码讲解课程和博文
格密码入门课程_哔哩哔哩_bilibili
格密码的基础概念_唠嗑!的博客-CSDN博客_格密码
格(Lattice)基础(一)_Amire0x的博客-CSDN博客_两组格基生成同一个格的充要条件
这篇关于格密码学习笔记(二):连续极小、覆盖半径和平滑参数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


