本文主要是介绍最少转机问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
分析:
1.深度优先更适合目标比较明确,以找到目标为主要目的的情况
2.广度优先更适合在不断扩大遍历范围时找到相对最优解的情况
因此这里选用BFS—广度优先遍历
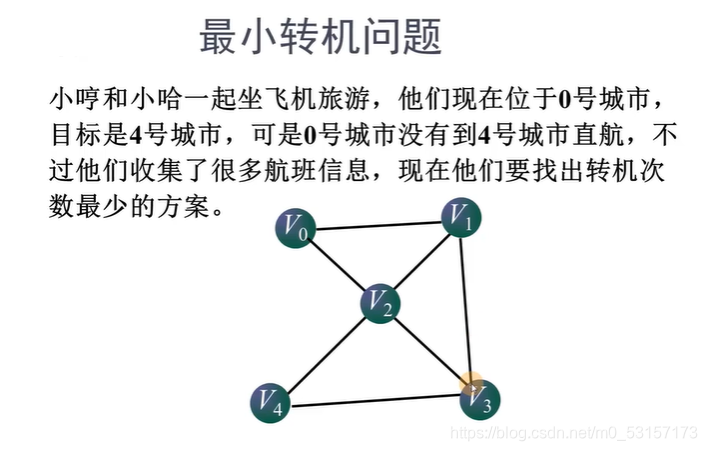
思路:这里要找到转机次数最少的方案,就是要寻找从V0顶点走到V4顶点的最短路径。
1.先列出哪些城市之间存在航线:(两顶点之间是否存在边)
v0------v1
v0------v2
v1------v2
v1------v3
v2------v3
v2------v4
v3------v4
2.进行广度优先遍历过程中,当所到达顶点为v4时,就退出广度优先遍历,此时得到的就是最少次数
用户输入四个值:存在几个城市 有几趟航线 起点城市 终点城市
返回:最少转机次数和转机方案
这里用01234来表示v0,v1,v2,v3,v4
#include<iostream>
using namespace std;
#include<queue>
const int MAX = 10; //图的最大顶点个数为10
typedef int DataType;
class Graph
{
private://边的个数int arcNum;//顶点个数int vertexNum;//定义一个存放顶点的一位数组DataType vertex[MAX];//定义一个存放顶点间的边关系的二维数组int arc[MAX][MAX];//访问数组int visit[MAX];
public://v[]数组存放用户输入的一维数组的顶点数据,n表示顶点个数,e是边的个数Graph(DataType v[], int n, int e,int VI[],int VJ[]);//BFS----广度优先遍历int BFS();
};
//有参构造函数的实现
Graph::Graph(DataType v[], int n, int e,int VI[],int VJ[])
{//初始化顶点个数vertexNum = n;//初始化边的个数arcNum = e;//初始化顶点数组for (int i = 0; i <n; i++){vertex[i] = v[i];}//初始化边数组for (int i = 0; i < MAX; i++)for (int j = 0; j < MAX; j++)arc[i][j] = 0;//初始化访问数组for (int i = 0; i < MAX; i++)visit[i] = 0;//一开始所有节点都处于未被访问的状态//由用户来决定,哪两个顶点之间存在边int vi=0, vj=0;for (int i = 0; i < arcNum; i++){//两个顶点之间的边关系int vi = VI[i];int vj = VJ[i];cout << vi << "<---->" << vj << endl;//这是无向图的边初始化标志arc[vi][vj] = 1;//有边的标志arc[vj][vi] = 1;}
}
//BFS-----广度优先遍历
int Graph::BFS()
{int num = 0;//记录转机次数queue<DataType> q;//队列存储的是顶点信息//外层for循环,检查是否每个节点都被访问过,防止存在节点未被访问过for (int i = 0; i < vertexNum; i++){if (visit[i]==0)//如果当前节点没有被访问过就进行处理{//设置当前节点被访问过visit[i] == 1;cout << vertex[i]<<" ";//说明找到了四号城市,退出当前遍历过程if (vertex[i] == 3){return num;}//将此顶点入队q.push(vertex[i]);//若当前队列不为空---表示当前顶点还存在邻接点没有被访问过while (!q.empty()){ q.pop();//队头元素出队//遍历当前顶点在邻接矩阵中当前行,找找是否存在未被访问过的顶点for (int j = 0; j < vertexNum; j++){//当前两个顶点之间有边 当前顶点的邻接点未被访问过if (arc[i][j] == 1 && visit[j] == 0){//将找到的此节点标志设置为已经访问visit[j] = 1;//输出这两个被边连接的顶点cout <<vertex[j] <<" ";//找到一个邻接点,次数++num++;//将找到的此节点入队//每次把当前顶点入队都是为了得到它的邻接点,并判断是否被访问过q.push(vertex[j]);}//找到的当前邻接点为4号城市,退出遍历if (vertex[j] == 3){return num;}}}}}//0号城市和4号城市之间不存在航线可以抵达return -1;
}
//测试-------------------
void test()
{//存储两个顶点之间边关系的数组int VI[14] = {0,0,2,2,2,3,3};int VJ[7] = { 1,2,1,4,3,1,4 };DataType v[5] = { 0,1,2,3,4 };cout << "存在航线的城市有:" << endl;Graph p(v, 5, 7,VI,VJ);cout << "输出所有城市:" << endl;int num=p.BFS();cout << endl;cout << "0号到3号城市之间的最少转机次数为:"<<num << endl;
}
int main()
{test();system("pause");return 0;
}
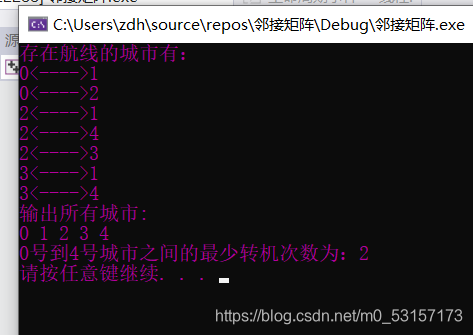
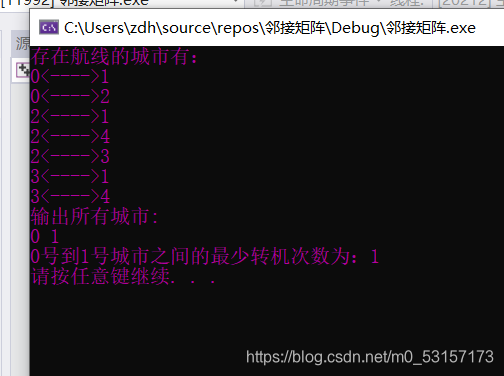
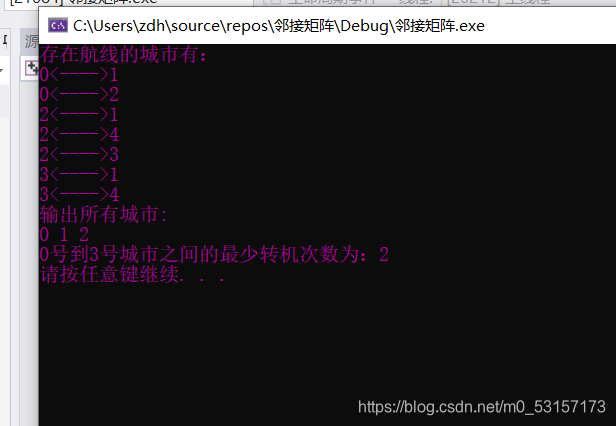
这篇关于最少转机问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





