图的知识点补充（AOE网络的关键路径）

本文主要是介绍图的知识点补充（AOE网络的关键路径），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一个无环的有向图称为无环图（Directed Acyclic Graph），简称DAG图。
AOE(Activity On Edge)网：顾名思义，用边表示活动的网，当然它也是DAG。与AOV不同，活动都表示在了边上，如下图所示：

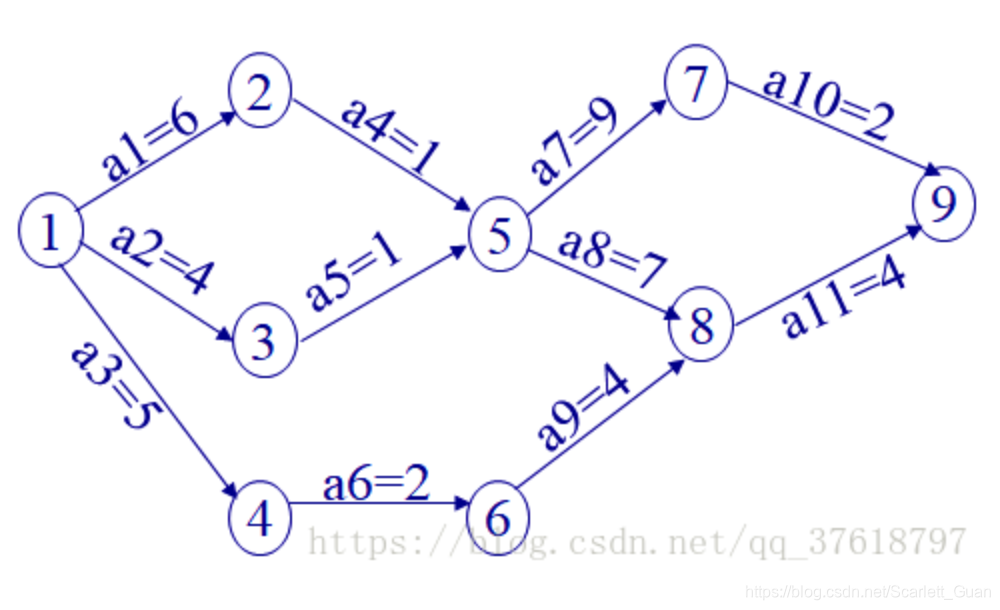
如上所示，共有11项活动（11条边），9个事件（9个顶点）。整个工程只有一个开始点和一个完成点。即只有一个入度为零的点（源点）和只有一个出度为零的点（汇点）。
关键路径：是从开始点到完成点的最长路径的长度。路径的长度是边上活动耗费的时间。如上图所示，1 到2 到 5到7到9是关键路径（关键路径不止一条，请输出字典序最小的），权值的和为18。

Input

这里有多组数据，保证不超过10组，保证只有一个源点和汇点。输入一个顶点数n(2<=n<=10000),边数m(1<=m <=50000),接下来m行，输入起点sv，终点ev,权值w（1<=sv,ev<=n,sv != ev,1<=w <=20)。数据保证图连通。

Output

关键路径的权值和，并且从源点输出关键路径上的路径（如果有多条，请输出字典序最小的）。

Sample Input

Sample Output

思路：这个题目实际上考查的是AOE网络的关键路径问题。

1、先了解一下AOE网络的关键路径的原理，请参考：经典算法之关键路径

2、具体计算步骤再细致地理一下：

Ev[i]表示事件i的最早出现时间，E[i]表示活动i的最早出现时间，Lv[i]表示事件i的最迟出现时间，L[i]表示活动i的最迟出现时间。

以j顶点指向k顶点为例：

（1）从源点开始向汇点递推，根据Ev[k]=max(Ev[j]+w[j,k])，求出Ev数组。其中的最大值Ev[n]是汇点的最早开始时间。

（2）因为汇点就是结束点，其最迟出现时间与最早出现时间相同，即Ev[n]=Lv[n]。将（1）中排好序的事件，从汇点开始向源点递推，根据Lv[j]=min(Lv[k]-w[j,k])，求出Lv数组。

（3）活动的最早开始时间与事件的最早开始时间是一样的，求出E数组，E=Ev.

（4）j顶点指向k顶点，中间经历活动aj, 根据L[j]=Lv[k]-(活动j所需的时间)，求出L数组。

（5）E[i]=L[i]的活动，就是关键活动，由这些活动组成的路径就是关键路径。

（6）有可能关键路径不止一条，那么这时候可以将re按照字典序排序，如果后一条路径的起始点，与前一条路径的结束点不一致，即x[i][0]!=x[i-1][1]，删后面的元素。

3、设计算法所用到的数据结构：

输入：m和n两个整数，一个二维数组G（G的长度应该和m是一样的），每个数组的元素是一个长度为3的一维数组，分别存一条边的两个顶点和权重。

输出：一个二维数组，每个数组的元素是一个长度为2的一维数组，分别存关键路径上每一条边的两个顶点。

（1）建一个长度为n（顶点数）的二维数组Event，每个数组的元素是一个长度为2的一维数组，分别存每个事件的Ev[i]和Lv[i]。

（2）建一个长度为m（边数）的二维数组Acti，每个数组的元素是一个长度为2的一维数组，分别存每个活动的E[i]和L[i]。

4、代码实现：

#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <unordered_map>
#include <sstream>
#include <stack>
#include <unordered_set>
#include <math.h>
using namespace std;vector<vector<int> > AOE(vector<vector<int> > &g, int n, int m) {//建一个长度为n（顶点数）的二维数组Event，每个数组的元素是一个长度为2的一维数组，分别存每个事件的Ev[i]和Lv[i]vector<vector<int> >Event(n + 1, vector<int>(2));//建一个长度为m（边数）的二维数组Acti，每个数组的元素是一个长度为2的一维数组，分别存每个活动的E[i]和L[i]vector<vector<int> >Acti(m, vector<int>(2));//把原图中的信息存在一个哈希表里面，方便查找unordered_map<int, unordered_map<int, int> >mm;for (auto x : g){mm[x[0]][x[1]] = x[2];}//从源点开始向汇点递推，根据Ev[k]=max(Ev[j]+w[j,k])，求出Ev数组,也就是Event数组每个元素x的x[0]for (int i = 1; i <= n; ++i){for (int j = 1; j < i; ++j){if (mm[j].count(i)){Event[i][0] = max(Event[i][0], Event[j][0] + mm[j][i]);}}}cout << endl << endl << "Event[i][0]:" << endl;for (auto x : Event){cout << x[0] << " ";}cout << endl;//从汇点开始向源点递推，根据Lv[j]=min(Lv[k]-w[j,k])，求出Lv数组,也就是Event数组每个元素x的x[1]for (auto &x : Event){x[1] = Event.back()[0];}for (int i = n - 1; i >=1; --i){for (int j = i + 1; j <= n; ++j){if (mm[i].count(j)){Event[i][1] = min(Event[i][1], Event[j][1] - mm[i][j]);}}}cout << endl << endl << "Event[i][1]:" << endl;for (auto x : Event){cout << x[1] << " ";}cout << endl;//活动的最早开始时间与事件的最早开始时间是一样的，求出E数组，也就是Acti数组每个元素x的x[0]for (int i = 0; i < m; ++i){Acti[i][0] = Event[g[i][0]][0];}cout << endl << endl << "Acti[i][0]:" << endl;for (auto x : Acti){cout << x[0] << " ";}cout << endl;//j顶点指向k顶点，中间经历活动aj, 根据L[j]=Lv[k]-(活动j所需的时间)，求出L数组,也就是Acti数组每个元素x的x[1]for (int i = m - 1; i >= 0; --i){Acti[i][1] = Event[g[i][1]][1] - g[i][2];}cout << endl << endl << "Acti[i][1]:" << endl;for (auto x : Acti){cout << x[1] << " ";}cout << endl;vector<vector<int> >re;//找出Acti数组中元素x的x[0]=x[1]的活动，就是关键活动for (int i = 0; i < Acti.size(); ++i){if (Acti[i][0] == Acti[i][1]){re.push_back({ g[i][0], g[i][1] });}}//题目中要求：如果有多条，请输出字典序最小的,所以还需要做点小处理:将re按照字典序排序，如果x[i][0]!=x[i-1][1],删后面的元素sort(re.begin(), re.end());for (int i = 1; i < re.size(); ++i){if (re[i][0] != re[i - 1][1]){re.erase(re.begin() + i);}}return re;
}int main()
{vector<vector<int> > g = { { 1, 2, 6 }, { 1, 3, 4 }, { 1, 4, 5 }, { 2, 5, 1 }, { 3, 5, 1 },{ 4, 6, 2 }, { 5, 7, 9 }, { 5, 8, 7 }, { 6, 8, 4 }, { 8, 9, 4 }, { 7, 9, 2 } };vector<vector<int> > re = AOE(g, 9, 11);cout << endl << endl << "关键路径:" << endl;for (auto x : re){for (auto y : x){cout << y << " ";}cout << endl;}return 0;
}

来一个只写函数的干净简洁版本：

vector<vector<int> > AOE(vector<vector<int> > &g, int n, int m) {//建一个长度为n（顶点数）的二维数组Event，每个数组的元素是一个长度为2的一维数组，分别存每个事件的Ev[i]和Lv[i]vector<vector<int> >Event(n + 1, vector<int>(2));//建一个长度为m（边数）的二维数组Acti，每个数组的元素是一个长度为2的一维数组，分别存每个活动的E[i]和L[i]vector<vector<int> >Acti(m, vector<int>(2));//把原图中的信息存在一个哈希表里面，方便查找unordered_map<int, unordered_map<int, int> >mm;for (auto x : g){mm[x[0]][x[1]] = x[2];}//从源点开始向汇点递推，根据Ev[k]=max(Ev[j]+w[j,k])，求出Ev数组,也就是Event数组每个元素x的x[0]for (int i = 1; i <= n; ++i){for (int j = 1; j < i; ++j){if (mm[j].count(i)){Event[i][0] = max(Event[i][0], Event[j][0] + mm[j][i]);}}}//从汇点开始向源点递推，根据Lv[j]=min(Lv[k]-w[j,k])，求出Lv数组,也就是Event数组每个元素x的x[1]for (auto &x : Event){x[1] = Event.back()[0];}for (int i = n - 1; i >=1; --i){for (int j = i + 1; j <= n; ++j){if (mm[i].count(j)){Event[i][1] = min(Event[i][1], Event[j][1] - mm[i][j]);}}}//活动的最早开始时间与事件的最早开始时间是一样的，求出E数组，也就是Acti数组每个元素x的x[0]for (int i = 0; i < m; ++i){Acti[i][0] = Event[g[i][0]][0];}//j顶点指向k顶点，中间经历活动aj, 根据L[j]=Lv[k]-(活动j所需的时间)，求出L数组,也就是Acti数组每个元素x的x[1]for (int i = m - 1; i >= 0; --i){Acti[i][1] = Event[g[i][1]][1] - g[i][2];}vector<vector<int> >re;//找出Acti数组中元素x的x[0]=x[1]的活动，就是关键活动for (int i = 0; i < Acti.size(); ++i){if (Acti[i][0] == Acti[i][1]){re.push_back({ g[i][0], g[i][1] });}}//题目中要求：如果有多条，请输出字典序最小的,所以还需要做点小处理:将re按照字典序排序，如果x[i][0]!=x[i-1][1],删后面的元素sort(re.begin(), re.end());for (int i = 1; i < re.size(); ++i){if (re[i][0] != re[i - 1][1]){re.erase(re.begin() + i);}}return re;
}

5、输出结果截图