QT通过起点、终点、弧度（方向）来绘制圆弧

Draws the arc defined by the given rectangle, startAngle and spanAngle.

The startAngle and spanAngle must be specified in 1/16th of a degree, i.e. a full circle equals 5760 (16 * 360). Positive values for the angles mean counter-clockwise while negative values mean the clockwise direction. Zero degrees is at the 3 o'clock position.

以上命令主要内容为需要通过一个给定的矩形和起始角、偏移角来绘制圆弧。起始角和偏移角必须必须是度数的十六分之一。即1°表示为1*16，直角90°表示为90*16。举例如下：

  QRectF rectangle(10.0, 20.0, 80.0, 60.0);    //给定的矩形，我们会直接用正方形来绘制正圆弧int startAngle = 30 * 16;    //起始角，以3点方向为0°，逆时针为整。int spanAngle = 120 * 16;    //偏移角，就是起始角和终止角的差值。绘制整个圆就输入360 * 16QPainter painter(this);painter.drawArc(rectangle, startAngle, spanAngle);    //调用绘图命令

上面例子绘出的圆弧为：

3.2 我们的程序如下，程序变量可能与上述代号不同，请注意体会

int Helper::caculateArcParameters(arcParameters * arcPara, inputParameters inputPara)
{//返回struct arcParameters指针，使用指针而不是直接返回arcParameters变量仅仅是因为可以判断是否为NULL。//判断是否可以做圆弧，否则返回空NULL//角度为0， 或者两点坐标重合，返回NULLdouble x1 = inputPara.x1;double y1 = inputPara.y1;double x2 = inputPara.x2;double y2 = inputPara.y2;double jiaoDu = inputPara.jiaoDu; //本段弧线的弧度或角度 θint yinYong = inputPara.yinYong;if ((jiaoDu == 0)or(yinYong != 0)or((x1 == x2)and(y1 == y2))){return 1; //当没有弧度，或者有引用时，或者两点坐标重合时，返回1。正确返回0，如下。}else{
//        double mx = (x1+x2)/2; double my = (y1+y2)/2;double L = qSqrt((x2-x1)*(x2-x1) + (y2-y1)*(y2-y1));    //两点之间距离。调试正确double R = qAbs((0.5 * L) / qSin(jiaoDu));    //圆弧所在圆的半径  qsin都是弧度，角度需要转换。double orginJiaoDu = qAtan((y2-y1)/(x2-x1));    //起点终点组成的角度ð（单位弧度）double C_x = x1 + R / qCos(qDegreesToRadians(90.0) - jiaoDu + orginJiaoDu);  //圆心坐标xdouble C_y = y1 + R / qSin(qDegreesToRadians(90.0) - jiaoDu + orginJiaoDu);   //弧度相互加减qDebug()<<"orginjiaoDu:"<<orginJiaoDu<<" jiaodu:"<<jiaoDu;qDebug()<<"\n R:"<<R;qDebug()<<"\n C_x:"<<C_x<<"  C_y:"<<C_y;arcPara->rectParameter = QRectF(C_x - R, C_y - R, 2 * R, 2 * R);arcPara->startAngleParameter = qRadiansToDegrees(qAtan((y2 - C_y)/(x2 - C_x))) * 16; //y方向取负值arcPara->spanAngleParameter = arcPara->startAngleParameter - qRadiansToDegrees(2 * jiaoDu) * 16;
//        arcPara->spanAngleParameter = 360 * 16;return 0;}
}

3.3 以上程序还在调试中，希望可以对大家啊有所帮助。

函数通过一个结构指针返回计算结果，通过一个结构传输数据，结构定义如下：

truct arcParameters
{QRectF rectParameter;int startAngleParameter;int spanAngleParameter;
};
struct inputParameters
{double x1;double y1;double x2;double y2;double jiaoDu;int yinYong;
};

3.4 程序运行效果

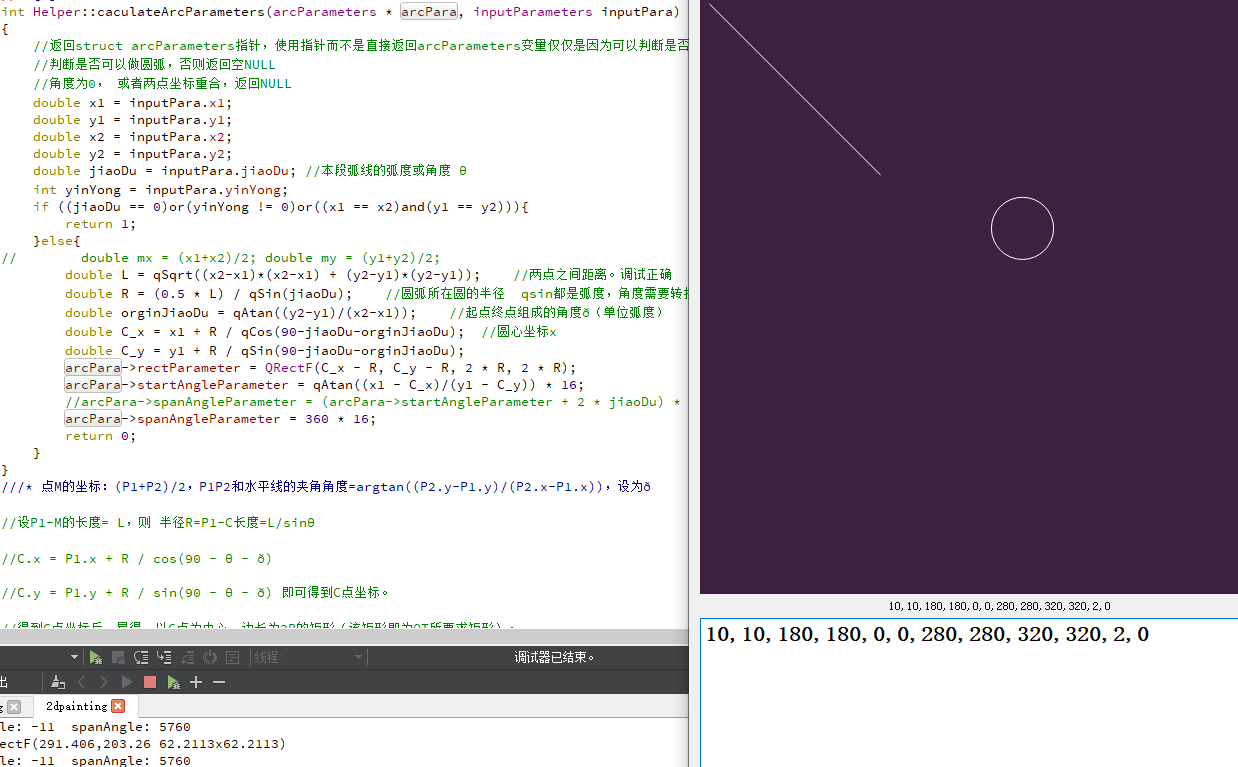
这个程序的运行效果如上，上面图形可以根据下面输入数据来绘图。 来定制绘图。

这么做的目的是通过文本来保存图形。

注，程序还在优化中。

4. 结束

4.1 经过不屑的努力，程序终于能正常运算了。主要困难再坐标转换和三角函数中出现的基础错误。整体思路没有问题。

最主要的函数如下，如果对您有帮助，还请多支持。

int Helper::caculateArcParameters(arcParameters * arcPara, inputParameters inputPara)
{//返回struct arcParameters指针，使用指针而不是直接返回arcParameters变量仅仅是因为可以判断是否为NULL。//判断是否可以做圆弧，否则返回空NULL//角度为0， 或者两点坐标重合，返回NULL//[1]输入数据为x-y坐标，角度不变（逆时针为正），并判断输入数据是否合理。double x1 = inputPara.x1;double y1 = inputPara.y1;double x2 = inputPara.x2;double y2 = inputPara.y2;double radianOfDirect = inputPara.direct; //本段弧线的弧度 θ，表示起点方向偏离P1P2方向的角度，逆时针为正。int id = inputPara.idOfRefer;const double radianOf90 = qDegreesToRadians(90.0);if ((radianOfDirect == 0)or(qAbs(radianOfDirect) >= radianOf90 * 2)){return 1;   //大于180度  = 0 时退出确保方向位于 （0--180)之间，不含0和180度。};if ((id != 0)or((x1 == x2)and(y1 == y2))){return 1;}; //退出函数, 否则继续下面语句//[2] 计算P1、P2和X轴角度angleOfP1P2、中点M坐标及向量(M,P1),(M,P2)长度; 和半径radiusdouble angleOfP1P2 = qDegreesToRadians(getAngle((x2 - x1),(y2 - y1)));double m_x = (x1+x2)/2;double m_y = (y1+y2)/2;
//    double vectorMp2_x = x2 - m_x;
//    double vectorMp2_y = y2 - m_y;double lengthOfMP2 = qSqrt((x2 - m_x)*(x2 - m_x) + (y2 - m_y)*(y2 - m_y));    //两点之间距离。调试正确double radius = qAbs(lengthOfMP2 / sin(radianOfDirect));double vectorP2N_x; //P2指向圆心的单位长度向量double vectorP2N_y;double angleOfStart;double angleOfSpan;double C_x = 0;double C_y = 0;//[3]根据角度正负，优弧劣弧分别计算圆心坐标C_x C_y。先算单位P2指向圆心的向量再乘以半径长度即可。if (radianOfDirect > 0){//角度大于0vectorP2N_x = cos(angleOfP1P2)*cos(-radianOfDirect - radianOf90) - sin(angleOfP1P2)*sin(-radianOfDirect - radianOf90);vectorP2N_y = sin(angleOfP1P2)*cos(-radianOfDirect - radianOf90) + cos(angleOfP1P2)*sin(-radianOfDirect - radianOf90);}else if (radianOfDirect < 0){//角度小于0vectorP2N_x = cos(angleOfP1P2)*cos(-radianOfDirect + radianOf90) - sin(angleOfP1P2)*sin(-radianOfDirect + radianOf90);vectorP2N_y = sin(angleOfP1P2)*cos(-radianOfDirect + radianOf90) + cos(angleOfP1P2)*sin(-radianOfDirect + radianOf90);}else{return 1;//应该不会执行。};//所有情况C坐标均等于P2 + P2N向量乘以倍率！C_x = x2 + vectorP2N_x * radius;C_y = y2 + vectorP2N_y * radius;qDebug()<<"P1P2-X角度:"<<angleOfP1P2<<" 圆弧弧度方向:"<<radianOfDirect;qDebug()<<"半径:"<<radius;qDebug()<<"C_x:"<<C_x<<"  C_y:"<<C_y;qDebug()<<"x1,y1:"<<x1<<"__"<<y1;qDebug()<<"x2,y2:"<<x2<<"__"<<y2;//[4]根据角度，分别计算起始角度和偏转角度
//    angleOfStart = 0;
//    angleOfSpan = 90;// 验证的确时再“第四”象限。/* ！！！坐标改为普通X-Y坐标后，角度的起始角度也有所变化。此时角度时逆时针旋转的！！！  */if (radianOfDirect > 0){//角度大于0，弧度向P1P2的左边弯曲，此时圆弧从P2到P1（顺时针）。angleOfStart = 360-getAngle((x1 - C_x), (y1 - C_y));// * 16;angleOfSpan = 360-getAngle((x2 - C_x), (y2 - C_y)) - angleOfStart;// * 16;}else if (radianOfDirect < 0){//角度小于0，与上面相反。圆弧为P1到P2angleOfStart = 360-getAngle((x2 - C_x), (y2 - C_y));// * 16;angleOfSpan = 360-getAngle((x1 - C_x), (y1 - C_y)) - angleOfStart;// * 16;}else{return 1;//应该不会执行。};//[5]把坐标Y值取负后，转换为y-x坐标，赋值给arcPara，返回0arcPara->rect = QRectF(C_x - radius, C_y - radius, 2 * radius, 2 * radius);qDebug()<<"StartAngle, SpanAngle:"<<angleOfStart<<"  "<<angleOfSpan;//    angleOfStart = 340;
//    angleOfSpan = 50;if (angleOfSpan < 0) angleOfSpan += 360;arcPara->angleOfStart = angleOfStart * 16;arcPara->angleOfSpan = angleOfSpan * 16;return 0;
};double Helper::getAngle(double x, double y) {double l = qSqrt(x*x + y*y);double a = qAcos(x/l);double ret = a * 180 / qDegreesToRadians(180.0); //弧度转角度，方便调试if (y < 0) {return 360 - ret;}return ret;
};

4.2 最终结果截图如下：

可以看出，不论P1 P2起始角如何变化，总能正确的绘制出圆弧。