通俗易懂的树状数组详解！请食用！qwq

本文主要是介绍通俗易懂的树状数组详解！请食用！qwq，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前：我写的线段树深受好评。于是想写树状数组。持续更新。

树状数组与二进制位有关。和线段树有些相像之处，都是把序列转化成一棵树进行操作。但是有区别。

update 2021.1.3:发现咕了接近2个月，决定写写

part 1 ：基本思想

1 二进制分解

如果1个数 $a$ 的二进制表示中，为1的为分别为：
$$a_{k,1},a_{k,2},a_{k,3}...a_{k,cnt}$$

则这个数=
$$2^{k,1}+2^{k,2}...+2^{k,cnt}$$

这就是二进制分解了。

2 树的由来

我们假设 $k_1>k_2>k_3...>k_{cnt}$,则区间 $[1,n]$ 可以被分成 $O(logn)$ 个小区间。

它们分别为：
$$[1,2^{k_1}],[2^{k_1}+1,2^{k_1}+2^{k_2}]...$$

于是有了一棵树。

3 小区间特点

如果区间结尾为 $r$,则区间长度就等于 $r$ 的二进制分解中最小的2的次幂。我们用函数 $lowbit$来求区间长度。

int lowbit(int x){return x & -x;}

有了这个函数，我们就可以用类似标记的整块修改来维护前缀和啦！！！

4 树的性质

我们用数组 $sum[x]$ 来保存序列 $a$ 的区间 $[x-lowbit(x)+1,x]$ 中所有数的和，则数组 $sum$ 就是一个树形结构。

这就是我们的树状数组啦！

图解：

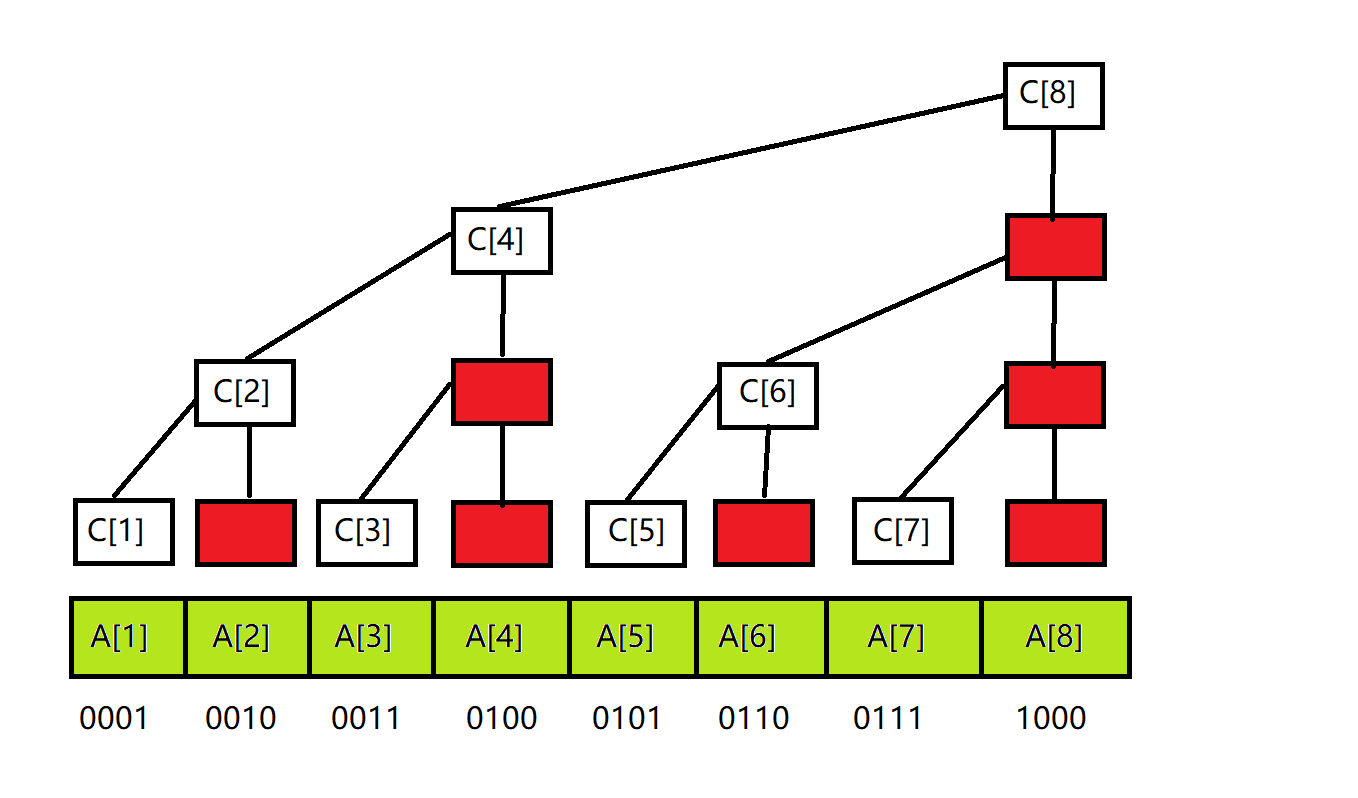
图中红色节点忽略不计qwq

在这个结构中：

1.每个节点保存以它为根的子树中所有叶节点的和

2.每个节点 $sum[x]$ 的子节点（指最底层的叶子结点！）个数等于 $lowbit(x)$ 的值。

笔者的书本上没有括号内容，然而我经过研究后发现，是指叶子结点的值。如4有1.2.3.4这4个叶子结点，对吧？所以 $lowbit(4)=4$ 。但是4有7个子节点（A4个，C3个）。

3.除了根节点，每个节点 $sum[x]$ 的父亲节点是 $sum[x+lowbit(x)]$

4.一整颗树的深度为 $O(logN)$。

基本思想讲完了！

part 2 ：常支持的操作

树状数组资瓷查询前缀和（自然可以区间和啦！），单点修改，求逆序对（和正序对），区间修改等。

好的，下一部分qwq。

part 3 ：代码

像这种数据结构（线段树，分块…）基本都有整体修改的标记，对吧qwq？

前缀和：

遍历一个节点的子树中的子节点，就可以了。

int ask(int x){int res=0;for(;x;x-=lowbit(x))res+=sum[x];return res;
} 

单点修改：

这个操作除了修改，还要维护前缀和，所以我们要对一个节点的祖先进行遍历，从下往上修改。这样子修改完，前缀和一定也是正确维护的。

void add(int x,int val){for(;x<=n;x+=lowbit(x))sum[x]+=val;
}//n为原始数列中元素个数 

区间修改：

我们新建一个数组 $b$，把一次区间修改（在区间 $[l,r]$ 中，把每一个值加上 $val$）转化为：

在 $b[l]$ 处加上 $val$，在 $b[r+1]$ 处减去 $val$。

原理是前缀和。在区间 $[1,l-1]$ 中，前缀和不变；在区间 $[l,r]$ 中，前缀和增加了 $val$；在区间 $[r+1,n]$ 中，前缀和不变（加 $val$ 和减去 $val$ 抵消）。

正确性使然。

这里的加是指单点修改。

不要直接 $sum[x]+=val$，会气死我的

区间和（区间查询）：

这种题的区间修改和上面类似，但是要改一下，因为还要执行区间和操作。我们使用两个树状数组 $c1$ 和 $c2$。

它们初始值为0。

对于修改区间 $[l,r]$，我们执行四次操作：

在 $c1$ 中，add(l,val);add(r+1,-val);

在 $c2$ 中，add(l,l*val);add(r+1,-(r+1)*val);

我们还要用 一个 数组储存数列原本的前缀和。

下面，对于每一个区间查询，我们分成1到 $r$ 和1到 $l-1$两个部分，查询结果就是二者相减。

int ask_lr(int l,int r){int ans=sum[r]+(r+1)*ask_c1(r)-ask_c2(r);ans-=(sum[l-1]+l*ask_c1(l-1)-ask_c2(l-1));return ans;
} //ask_c1是对c1的操作，ask_c2是对c2的操作，sum记录原始前缀和

这个式子好好理解下吧！

讲完啦！（注意：根据不同的题目，大部分时候请开long long）

part 4 ：练习题

一个比较不错的题单，做做吧

结：

写了怎么久，终于写完啦！

谢谢阅读。

这篇关于通俗易懂的树状数组详解！请食用！qwq的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---