本文主要是介绍信号类型(通信)——QAM调制信号,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
系列文章目录
《信号类型(通信)——仿真》
文章目录
前言
一、原理图
二、仿真
2.1、QAM仿真
2.2、不同滚降系数
2.3、不同M下QAM调制对比
总结
前言
本文主要结合仿真分析了QAM的信号处理过程,并简单分析了成型滤波器中的滚降系数对QAM的影响。
一、原理图
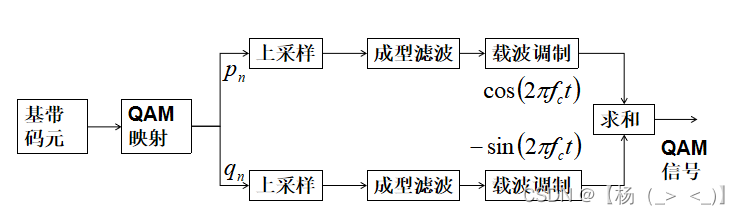
QAM信号调制的原理框图
QAM信号产生过程:基带码元波形经过QAM映射(串并转换分成I、Q两路,然后再经过电平转换,以16QAM为例,00转换成-0.5,01转换成-1.5,10转换成0.5,11转换成1.5)得到QAM调制信号,再与对应的载波相乘,然后再相加完成QAM的调制。
其中,
,
为载频,
为QAM调制码的IQ表示,
为码宽,
为码波形,由成型滤波器决定。
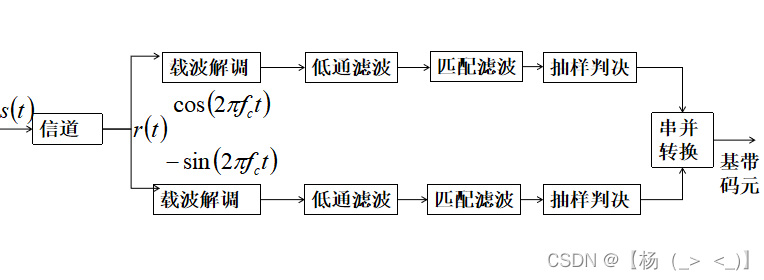
QAM信号解调的原理框图
QAM信号再分为I、Q两路和对应的载波相乘,然后经过低通滤波器得到基带信号:
其中,
表示接收机噪声,
分别表示IQ路噪声。
对下变频后的基带信号进行匹配滤波,并进行抽样判决,恢复出原始的码元序列。
二、仿真
参数设置,符号速率60kHz,采样率12 Mz,载频 1.5MHz,码序列随机生成,成型滤波器采用根升余弦滤波器,滚降系数决定码波形,QAM调制,M=4,16,64。部分代码如下:
%% 信号参数
rate = 6e4; % 符号速率
sample = 200; % 每个符号的采样点数
fc = 1.5e6; % 载波频率
fs = rate*sample; % 采样频率=比特率*每个符号的采样点数
M = 4; % 4,16,64
num = 100; % 帧数
symbol_number = 100; % 每帧发送数据符号个数
source_number = symbol_number*log2(M); % 发送信号的长度,bit数
rollof_factor1 = 0.8; % 发射滚降因子,可调整
N1 = 8;
rollof_factor2 = 0.8; % 接收滚降因子,可调整
N2 = 8;
rcos_fir1 = rcosdesign(rollof_factor1,N1,sample,'sqrt'); % 默认'sqrt'
rcos_fir2 = rcosdesign(rollof_factor2,N2,sample,'sqrt');%% 随机数据流生成
[frame_bit ,ns]= data_producing(M,source_number,num);%% QAM信号生成
% QAM映射
frame_msg = reshape(frame_bit,2,round(ns*num/2));
[qam_I,qam_Q]=qam1(frame_msg,M);% 成型滤波
[It_rcos,Qt_rcos]=qam2(qam_I,qam_Q,sample,rcos_fir1);% 载波调制
st = qam3(It_rcos,Qt_rcos,fc,fs);figure;
subplot(211)
stem(frame_msg(1,1:200));
xlabel('码序列');
ylabel('I路数据流');
subplot(212);
stem(frame_msg(2,1:200));
xlabel('码序列');
ylabel('Q路数据流');figure;
subplot(211);plot(It_rcos(1:200*sample));
xlabel('时间点数')
title('发射I路通过成型滤波器的时域波形');
subplot(212);plot(Qt_rcos(1:200*sample));
xlabel('时间点数')
title('发射Q路通过成型滤波器的时域波形');figure;
subplot(211);plot(st(1:200*sample));
title('载波调制时域波形');
xlabel('时间点数')
subplot(212);plot(linspace(-fs/2,fs/2,length(st)),abs(fftshift(fft(st))));
xlabel('频率(Hz)')
title('载波调制频域波形');%% 接收信号
% 高斯白噪声信道
snr = 15;
rt = awgn(st,snr,'measured');% IQ下变频
rt1=deqam1(rt,fc,fs);% 匹配滤波
rt2=deqam2(rt1,rcos_fir2);figure;
subplot(211);plot(rt(1:200*sample));
xlabel('时间点数')
title('接收时域波形');
subplot(212);plot(linspace(-fs/2,fs/2,length(st)),abs(fftshift(fft(rt))));
xlabel('频率(Hz)')
title('接收频谱');figure;
subplot(211);plot(real(rt1(1:200*sample)));
xlabel('时间点数')
title('接收解调后I路时域波形');
subplot(212);plot(imag(rt1(1:200*sample)));
xlabel('时间点数')
title('接收解调后Q路时域波形');figure;
subplot(211);plot(real(rt2(1:200*sample)));
xlabel('时间点数')
title('接收I路通过匹配滤波器的时域波形');
subplot(212);plot(imag(rt2(1:200*sample)));
xlabel('时间点数')
title('接收Q路通过匹配滤波器的时域波形');%% 直接解码
Cd1 = deqam3(rt1,1/max(rcos_fir1),sample,M);figure;
plot(frame_msg(:)-Cd1(:));
disp(sum(frame_msg(:)-Cd1(:)~=0)/length(Cd1(:)));
scatterplot(rt1(sample/2:sample:end)/max(rcos_fir1)); %星座图
title('匹配滤波后星座图');%% 匹配滤波后解码
Cd2 = deqam3(rt2,1,sample,M);figure;
plot(frame_msg(:)-Cd2(:));
disp(sum(frame_msg(:)-Cd2(:)~=0)/length(Cd2(:)));
scatterplot(rt2(sample/2:sample:end)); %星座图
title('匹配滤波后星座图');%% 眼图
% 匹配前
figure
plot(reshape(real(rt1(sample/2+1:sample/2+sample*200*2)),sample*2,200));
xlabel('时间点数')
title('匹配滤波前眼图');% 匹配后
figure
plot(reshape(real(rt2(sample/2+1:sample/2+sample*200*2)),sample*2,200));
xlabel('时间点数')
title('匹配滤波后眼图');2.1、QAM仿真
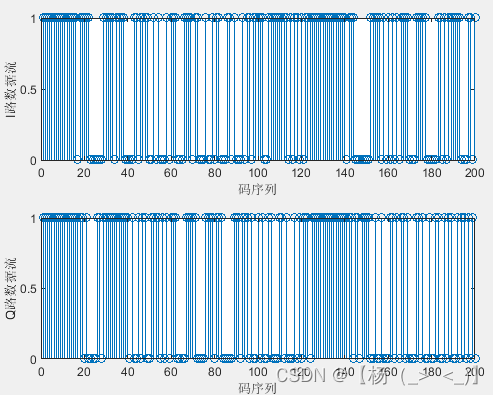
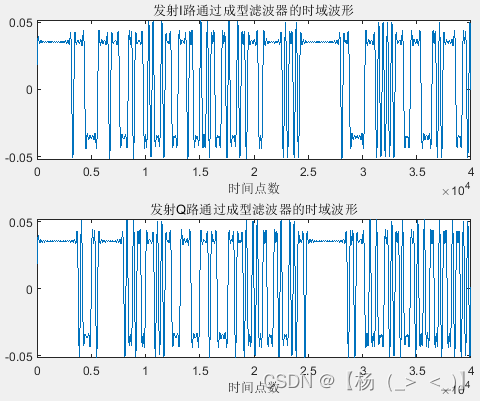
码序列 成型滤波后基带信号
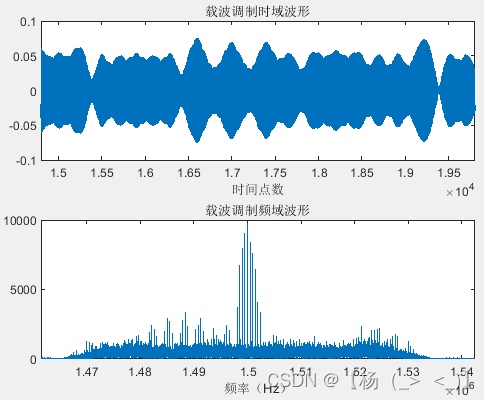
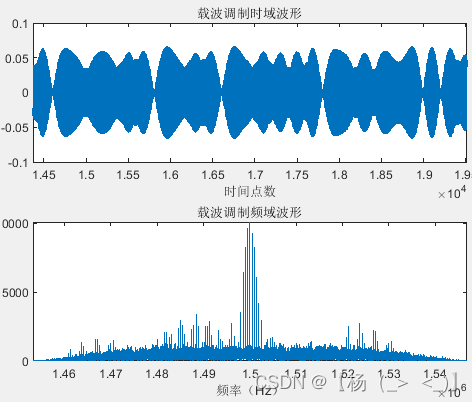
帧信号由帧头,帧体和帧尾构成,帧头和帧尾固定,帧体数据随机生成,生成的码序列如左上图所示。成型滤波器滚降系数0.8,码长8,对码脉冲信号进行成型滤波,得到右上图所示的基带信号。最后载频调制得到最终发射信号,如下图所示。
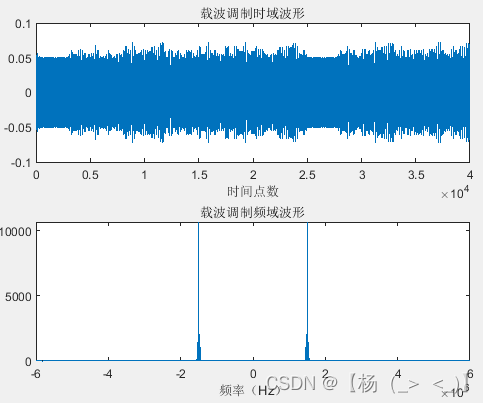
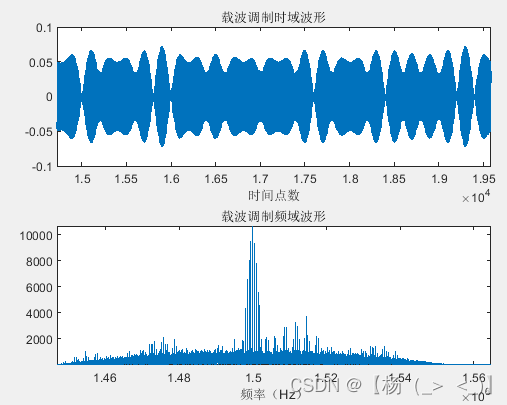
发射的射频信号波形以及频谱
只考虑接收机的热噪声影响,得到如下所示接收信号。与发射信号相比,信号波形存在随机波动。
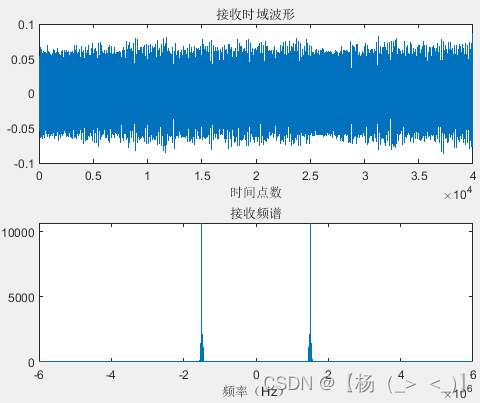
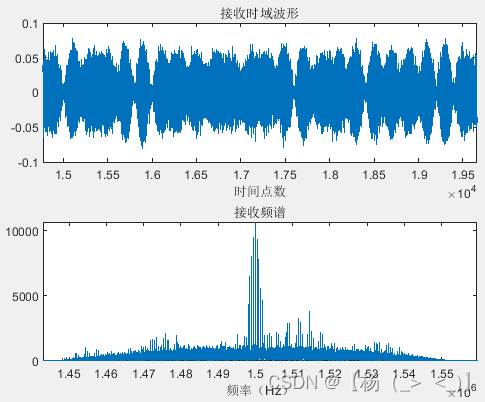
接收的射频信号波形以及频谱
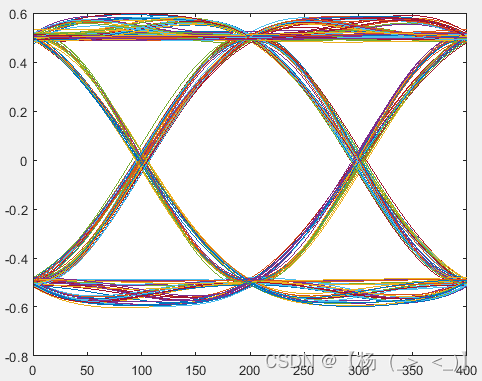
对接收的信号进行下变频至基带得到左下1图的基带信号,通过对信号进行截断得到左下2图所示的眼图,并基于最佳点得到左下3图所示的眼图。
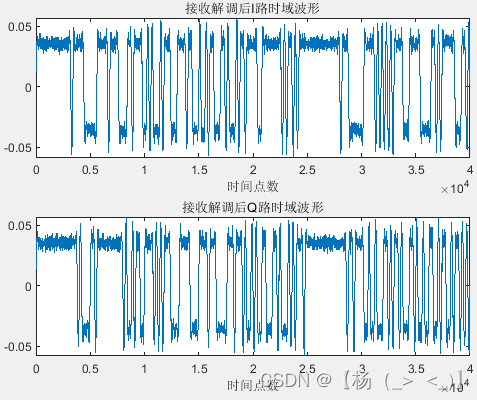
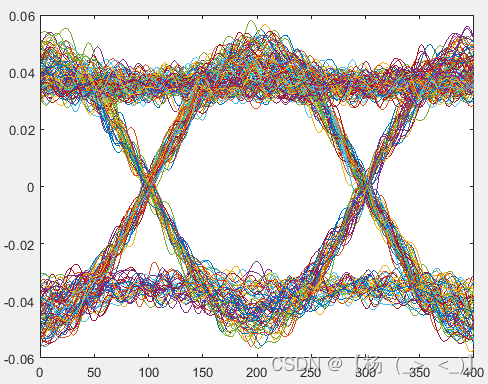
下变频后基带信号的波形,眼图以及基于最佳点的星座图
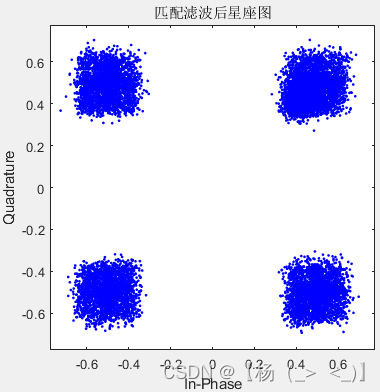
对下变频后的基带信号进行匹配滤波得到左下1图的基带信号,通过对信号进行截断得到左下2图所示的眼图,并基于最佳点得到左下3图所示的眼图。与匹配滤波前相比,信号的眼图以及星座图得到明显改善。
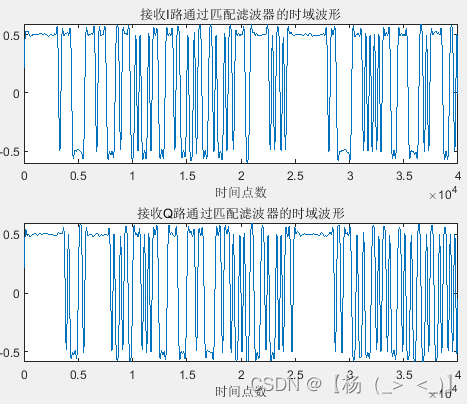
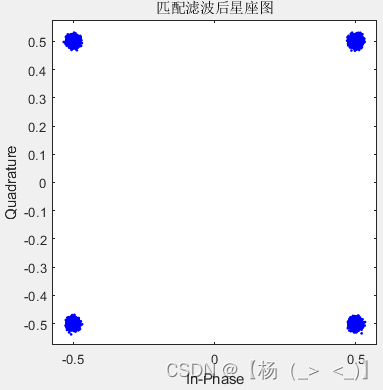
匹配滤波后基带信号的波形,眼图以及基于最佳点的星座图
2.2、不同滚降系数

0.05 0.5 0.8
发射的射频信号波形以及频谱
上图分别不同滚降系数下的发射信号波形以及对应的单边谱,可以看出随着滚降系数增加,信号波形越窄。
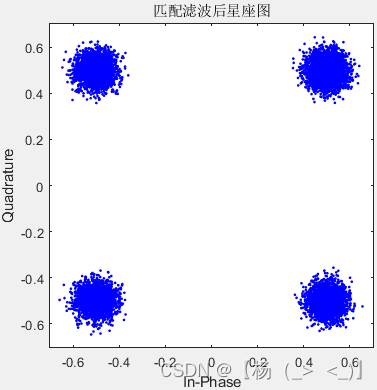
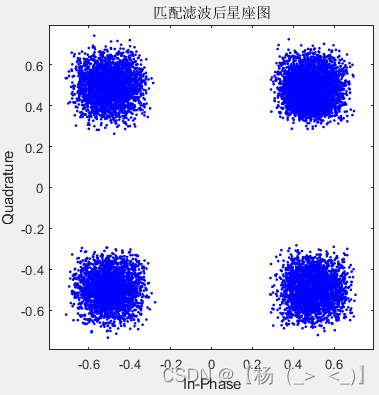

0.05 0.5 0.8
匹配滤波后基于最佳点的星座图
在不知道发射端的成型滤波器时,直接对下变频的接收信号进行检测,得到上图所示星座图,可以看出,滚降系数增加,对应的星座图逐渐恶化。
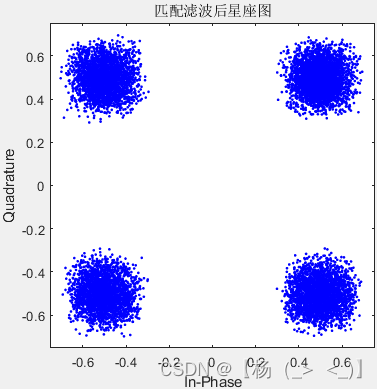
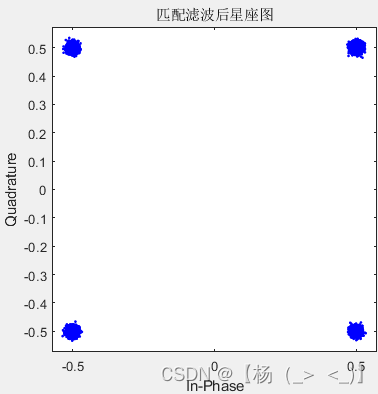

0.05 0.5 0.8
匹配滤波后基于最佳点的星座图
在发射端的成型滤波器已知情况时,可以对接收的基带信号进行匹配滤波,由此可以得到上图所示星座图,可以看出,滚降系数很小时,匹配滤波并没有改善星座图,但随着滚降系数的增肌,匹配滤波的效果也逐渐显现。
2.3、不同M下QAM调制对比

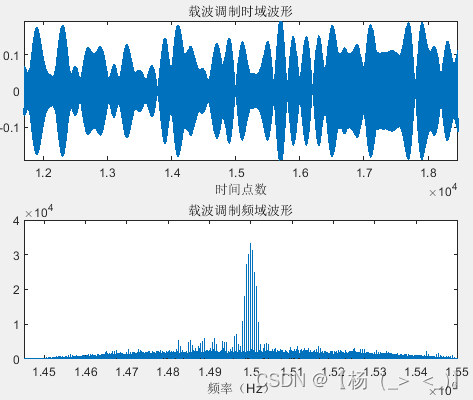
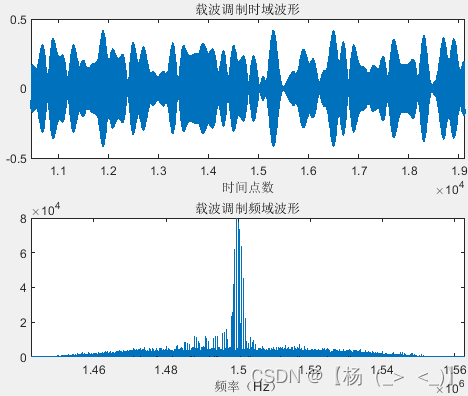
M=4 M=16 M=64
发射的射频信号波形以及频谱
上图分别维4QAM,16QAM以及64QAM调制的发射信号波形以及对应的单边谱,可以看出随着M增加,信号包络越加复杂,这种复杂的包络也意味着有着更多的信息被传递。

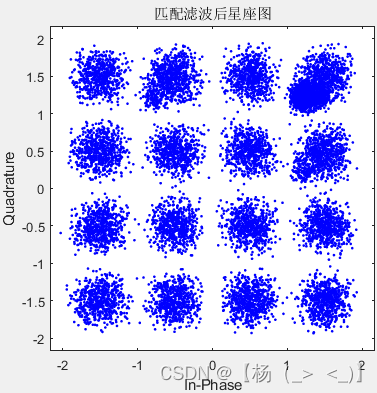
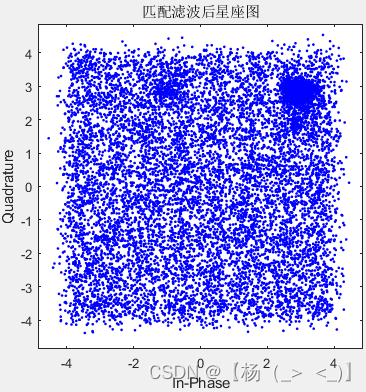
M=4 M=16 M=64
匹配滤波后基于最佳点的星座图
在不知道发射端的成型滤波器时,直接对下变频的接收信号进行检测,得到上图所示星座图,可以看出,随着M增加,对应的星座图逐渐恶化。

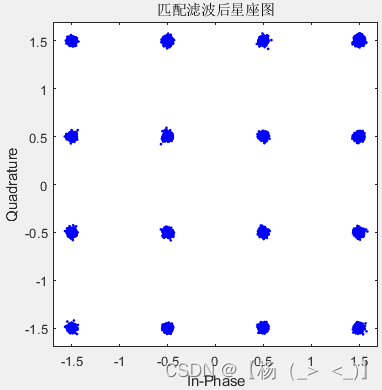
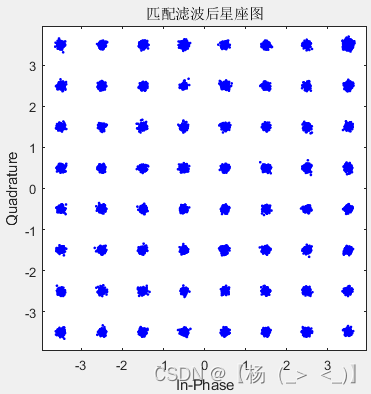
M=4 M=16 M=64
匹配滤波后基于最佳点的星座图
在发射端的成型滤波器已知情况时,可以对接收的基带信号进行匹配滤波,由此可以得到上图所示星座图,可以看出,匹配滤波能够明显改善星座图。
代码链接《通信+数字通信+QAM调制解调分析》;
总结
本文主要从仿真的角度简单分析了QAM调制解调过程,实际环境中的多普勒效应以及多径效应等并没有考虑。有更好的内容欢迎在评论区放置链接,另外有问题也欢迎评论区留言。转载请附链接【杨(_> <_)】的博客_CSDN博客-信号处理,SAR,代码实现领域博主。
这篇关于信号类型(通信)——QAM调制信号的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



